Difference between revisions of "Lattice:BCC"
KevinYager (talk | contribs) (→Reciprocal-space Peaks) |
KevinYager (talk | contribs) (→Examples) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
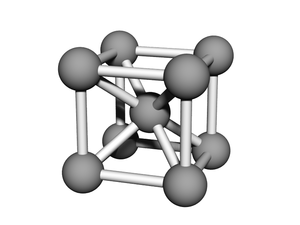
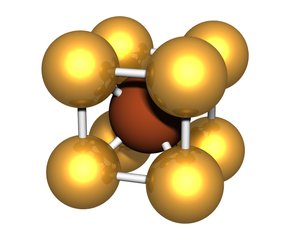
'''BCC''' or '''body-centered cubic''' is a cubic [[lattice]] where the symmetry involves an atom/particle sitting in the center of the conceptual [[unit cell]]. | '''BCC''' or '''body-centered cubic''' is a cubic [[lattice]] where the symmetry involves an atom/particle sitting in the center of the conceptual [[unit cell]]. | ||
| + | |||
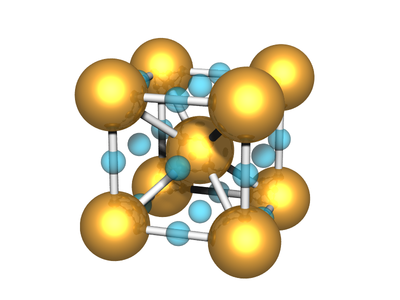
| + | [[Image:Bcc02-unit cell.png|thumb|right|300px|BCC unit cell.]] | ||
| + | |||
==Canonical BCC== | ==Canonical BCC== | ||
===Symmetry=== | ===Symmetry=== | ||
| Line 95: | Line 98: | ||
===[[Realspace]] Spacings=== | ===[[Realspace]] Spacings=== | ||
| − | [[Q value|Since]] <math>q=2 \pi / d</math>, the realspace spacing of planes is: | + | Note that in general: |
| + | :<math> | ||
| + | \begin{alignat}{2} | ||
| + | \left( \frac{1}{d_{hkl}} \right )^2 = \left(\frac{h}{a}\right)^2 + \left(\frac{k}{b}\right)^2 + \left(\frac{l}{c}\right)^2 | ||
| + | \end{alignat} | ||
| + | </math> | ||
| + | |||
| + | [[Q value|Since]] <math>q=2 \pi / d</math>, and since <math>a=b=c</math>, the realspace spacing of planes is: | ||
:<math> | :<math> | ||
\begin{alignat}{2} | \begin{alignat}{2} | ||
| − | + | d_{hkl} | |
| − | & = | + | & = \frac{a}{\sqrt{ h^2 + k^2 + l^2 }} |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\end{alignat} | \end{alignat} | ||
</math> | </math> | ||
| Line 150: | Line 155: | ||
===Examples=== | ===Examples=== | ||
| − | ==== | + | ====Atomic==== |
* [http://en.wikipedia.org/wiki/Cesium_chloride Cesium chloride (CsCl)] (''a'' = 4.11 Å) | * [http://en.wikipedia.org/wiki/Cesium_chloride Cesium chloride (CsCl)] (''a'' = 4.11 Å) | ||
Latest revision as of 13:50, 15 October 2014
BCC or body-centered cubic is a cubic lattice where the symmetry involves an atom/particle sitting in the center of the conceptual unit cell.
Contents
Canonical BCC
Symmetry
- Crystal Family: Cubic
- Crystal System: Cubic
- Bravais Lattice: I (bcc)
- Crystal class: Hexoctahedral
- Point Group: m3m
- Space Group: Im3m
- Particles per unit cell:
- Volume of unit cell:
- Dimensionality:
- Projected d-dimensional volume:
- Solid angle:
- Nearest-neighbor distance:
- Assuming spherical particles of radius R:
- Particle volume fraction:
- Maximum volume fraction: when
Structure
Body-centered cubic (BCC) is a cubic lattice where a cube-shaped unit cell has particles at each corner of the cube, plus a particle in the center of this cube. The minimal unit cell has only two particles.
The extended lattice can be thought of in terms of two inter-penetrating simple cubic lattices:
One can also consider the BCC to be a distorted FCC:
Neighbors
Each particle is equivalent (there is nothing special about the 'center' particle in a homogeneous BCC). For a lattice of edge-length a, each particle has 8 "diagonal" nearest-neighbors at a distance of:
and another 6 "direct" next-nearest-neighbors at a distance of .
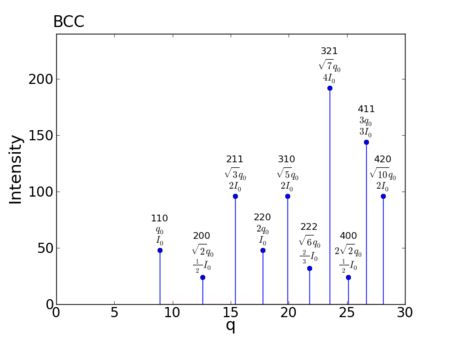
Reciprocal-space Peaks
- Allowed reflections:
- Peak multiplicities:
- Peak positions:
- For a = 1.0:
peak q value h,k,l m f intensity 1: 8.885765876317 1,1,0 12 2 48 2: 12.566370614359 2,0,0 6 2 24 3: 15.390597961942 2,1,1 24 2 96 4: 17.771531752633 2,2,0 12 2 48 5: 19.869176531592 3,1,0 24 2 96 6: 21.765592370811 2,2,2 8 2 32 7: 23.509526717078 3,2,1 48 2 192 8: 25.132741228718 4,0,0 6 2 24 9: 26.657297628950 4,1,1 36 2 144 10: 28.099258924163 4,2,0 24 2 96 11: 29.470751386686 3,3,2 24 2 96 12: 30.781195923885 4,2,2 24 2 96 13: 32.038084488828 5,1,0 72 2 288 14: 34.414423257273 5,2,1 48 2 192 15: 35.543063505267 4,4,0 12 2 48 16: 36.636951272563 5,3,0 48 2 192 17: 37.699111843078 6,0,0 30 2 120 18: 38.732155490827 6,1,1 72 2 288 19: 39.738353063184 6,2,0 24 2 96 20: 40.719694735877 5,4,1 48 2 192 21: 41.677936304377 6,2,2 24 2 96 22: 42.614636098416 6,3,1 48 2 192 23: 43.531184741621 4,4,4 8 2 32 24: 44.428829381584 5,5,0 60 2 240 25: 45.308693596556 6,4,0 24 2 96 26: 46.171793885827 6,3,3 48 2 192 27: 47.019053434156 6,4,2 48 2 192 28: 49.473850582607 6,5,1 48 2 192 29: 51.044838738971 5,5,4 24 2 96 30: 51.812473373661 6,4,4 24 2 96 31: 52.568899858234 6,5,3 48 2 192 32: 53.314595257900 6,6,0 12 2 48 33: 54.775539595071 6,6,2 24 2 96 34: 58.267863475287 6,5,5 24 2 96 35: 58.941502773372 6,6,4 24 2 96 36: 65.296777112432 6,6,6 8 2 32
Realspace Spacings
Note that in general:
Since , and since , the realspace spacing of planes is:
Examples
Elemental
- 3. Lithium (Li) (a = 3.509 Å)
- 11. Sodium (Na) (a = 4.291 Å)
- 19. Potassium( K) (a = 5.247 Å) (at 78 K)
- 23. Vanadium (V) (a = 3.024 Å)
- 24. Chromium (Cr) (a = 2.884 Å)
- 26. Iron (Fe) (a = 2.866 Å)
- 37. Rubidium (Rb) (a = 5.605 Å) (at 78 K)
- 41. Niobium (Nb) (a = 3.300 Å)
- 42. Molybdenum (Mo) (a = 3.147 Å)
- 55. Caesium (Cs) (a = 6.067 Å) (at 78 K)
- 56. Barium (Ba) (a = 5.025 Å)
- 63. Europium (Eu) (a = 4.606 Å)
- 73. Tantalum (Ta) (a = 3.306 Å)
- 74. Tungsten (W) (a = 3.165 Å)
Atomic
- TBD
Nano
- TBD
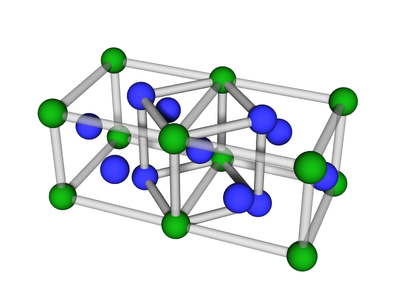
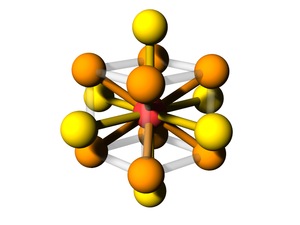
Body-centered Two-particle
A lattice where the unit cell has two distinct atoms/particles, arranged with one at the center of the simple cubic lattice defined by the other, has simple cubic symmetry. This lattice is often called CsCl.
Symmetry
- Crystal Family: Cubic
- Crystal System: Cubic
- Bravais Lattice: P (pcc)
- Crystal class: Hexoctahedral
- Point Group: m3m
- Space Group: Pm3m
- Particles per unit cell: (distinct)
- Volume of unit cell:
- Dimensionality:
- Projected d-dimensional volume:
- Solid angle:
- Nearest-neighbor distance:
Examples
Atomic
- Cesium chloride (CsCl) (a = 4.11 Å)
Body-centered with Edges and Faces
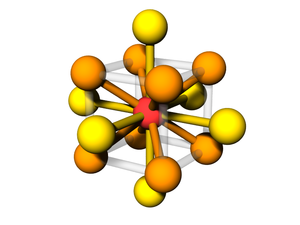
The BCC lattice, where a second particle type occupies positions along edges and faces. The symmetry is the same as the canonical BCC. (The particles at the face position are effective 'edge' particles with respect to the center particle...)
Particle Positions
There are 27 positions, with 8 particles in the unit cell
Particle A
These are the usual BCC positions. There are 9 positions. In total there are 2 particles in the unit cell:
Particle B
There are 18 positions, with 6 particles in the unit cell.