Circular orientation distribution function

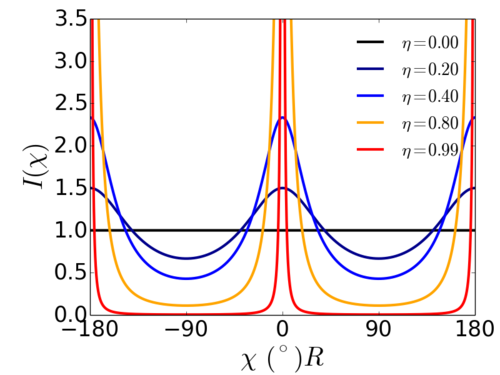
In assessing the orientation of aligned materials, one can use the orientation order parameter to quantify order. Another possibility is to fit scattering data using an equation that has 'circular wrapping' (i.e. periodic along $\scriptstyle 2\pi$).

$\eta$ function

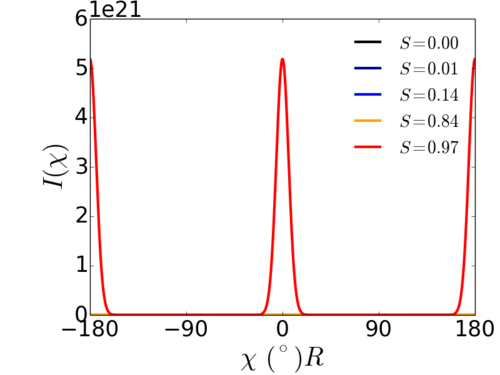
Ruland et al. present such an equation:

$I(\chi )={\frac {1-\eta ^{2}}{(1+\eta )^{2}-4\eta \cos ^{2}\chi }}$

Where $\scriptstyle \chi$ is the angle along the arc of the scattering ring/feature. The single fit parameter ($\scriptstyle \eta$) is convenient in that it behaves in a similar way to an order parameter: a value close to 1.0 indicates strong alignment, while progressively smaller values indicate lesser alignment. For a random sample, the scattering is isotropic and $\scriptstyle \eta =0$.

References

• Ruland, W.; Tompa, H., The Effect of Preferred Orientation on the Intensity Distribution of (Hk) Interferences. Acta Crystallographica Section A 1968, 24, 93-99.
• Ruland, W.; Smarsly, B., Saxs of Self-Assembled Oriented Lamellar Nanocomposite Films: An Advanced Method of Evaluation. J. Appl. Crystallogr. 2004, 37, 575-584.

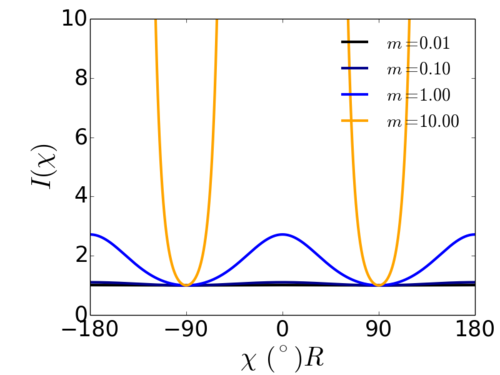
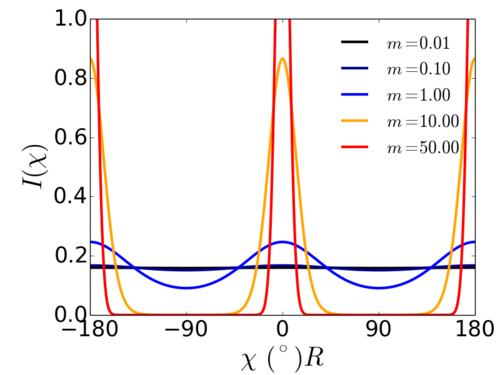
Maier-Saupe distribution parameter

$I(\chi )={\frac {1}{c}}\exp \left[m\cos ^{2}\chi \right]$

Where $\scriptstyle m$ is a parameter that can be related to the order parameter $\scriptstyle S$; specifically $\scriptstyle m=0$ is for an isotropic distribution ($\scriptstyle S=0$), while $\scriptstyle m\to \infty$ is for a well-aligned system ($\scriptstyle S\to 1$).

The parameter c can be used to normalize:

References

• B. J. Lemaire, P. Panine, J. C. P. Gabriel and P. Davidson The measurement by SAXS of the nematic order parameter of laponite gels Europhysics Letters 2002, 59 (1), 55-61.
• Maier W. and Saupe A., Z. Naturforsch. A, 13 (1958) 564; 14 (1959) 882; 15 (1960) 287.