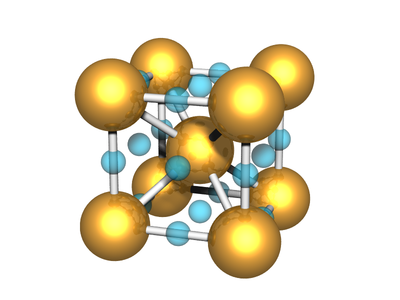
Lattice:BCC

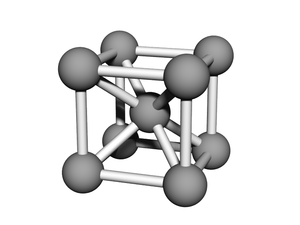
BCC or body-centered cubic is a cubic lattice where the symmetry involves an atom/particle sitting in the center of the conceptual unit cell.

Canonical BCC

Symmetry

• Crystal Family: Cubic
• Crystal System: Cubic
• Bravais Lattice: I (bcc)
• Crystal class: Hexoctahedral
• Point Group: m3m
• Space Group: Im3m
• Particles per unit cell: $n=2$
• Volume of unit cell: $V_{d}=a^{3}$
• Dimensionality: $d=3$
• Projected d-dimensional volume: $v_{d}=a^{3}$
• Solid angle: $\Omega _{d}=4\pi$
• Nearest-neighbor distance: $d_{nn}={\sqrt {3}}a/2$
• Assuming spherical particles of radius R:
  • Particle volume fraction: $\phi =8\pi R^{3}/\left(3a^{3}\right)$
  • Maximum volume fraction: $\phi _{max}=\pi {\sqrt {3}}/8\approx 0.680$ when $R=a{\sqrt {3}}/4$

Structure

Body-centered cubic (BCC) is a cubic lattice where a cube-shaped unit cell has particles at each corner of the cube, plus a particle in the center of this cube. The minimal unit cell has only two particles.

The extended lattice can be thought of in terms of two inter-penetrating simple cubic lattices:

One can also consider the BCC to be a distorted FCC:

Neighbors

Each particle is equivalent (there is nothing special about the 'center' particle in a homogeneous BCC). For a lattice of edge-length a, each particle has 8 "diagonal" nearest-neighbors at a distance of:

$d_{\mathrm {nn} }={\sqrt {3}}/2\times a\approx 0.866a$

and another 6 "direct" next-nearest-neighbors at a distance of $a=(2/{\sqrt {3}})d_{nn}$.

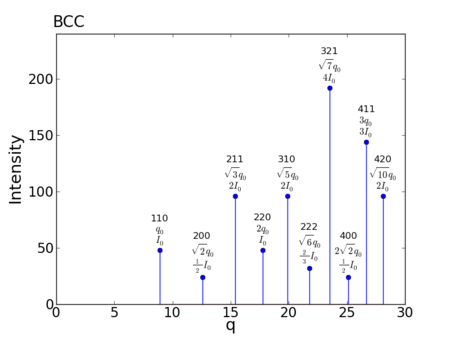
Reciprocal-space Peaks

• Allowed reflections:

  $f_{hkl}=2\,\,\,\mathrm {for} \,\,\,h+k+l=\mathrm {even}$

• Peak multiplicities:

  $m_{h00}=6$

  $m_{hh0}=12$

  $m_{hhh}=8$

  $m_{hk0}=24$

  $m_{hhk}=24$

  $m_{hkl}=48$

• Peak positions:

  $q_{hkl}={\frac {2\pi }{a}}{\sqrt {h^{2}+k^{2}+l^{2}}}$

  For a = 1.0:

peak    q value         h,k,l   m       f       intensity
1:      8.885765876317  1,1,0   12      2       48
2:      12.566370614359 2,0,0   6       2       24
3:      15.390597961942 2,1,1   24      2       96
4:      17.771531752633 2,2,0   12      2       48
5:      19.869176531592 3,1,0   24      2       96
6:      21.765592370811 2,2,2   8       2       32
7:      23.509526717078 3,2,1   48      2       192
8:      25.132741228718 4,0,0   6       2       24
9:      26.657297628950 4,1,1   36      2       144
10:     28.099258924163 4,2,0   24      2       96
11:     29.470751386686 3,3,2   24      2       96
12:     30.781195923885 4,2,2   24      2       96
13:     32.038084488828 5,1,0   72      2       288
14:     34.414423257273 5,2,1   48      2       192
15:     35.543063505267 4,4,0   12      2       48
16:     36.636951272563 5,3,0   48      2       192
17:     37.699111843078 6,0,0   30      2       120
18:     38.732155490827 6,1,1   72      2       288
19:     39.738353063184 6,2,0   24      2       96
20:     40.719694735877 5,4,1   48      2       192
21:     41.677936304377 6,2,2   24      2       96
22:     42.614636098416 6,3,1   48      2       192
23:     43.531184741621 4,4,4   8       2       32
24:     44.428829381584 5,5,0   60      2       240
25:     45.308693596556 6,4,0   24      2       96
26:     46.171793885827 6,3,3   48      2       192
27:     47.019053434156 6,4,2   48      2       192
28:     49.473850582607 6,5,1   48      2       192
29:     51.044838738971 5,5,4   24      2       96
30:     51.812473373661 6,4,4   24      2       96
31:     52.568899858234 6,5,3   48      2       192
32:     53.314595257900 6,6,0   12      2       48
33:     54.775539595071 6,6,2   24      2       96
34:     58.267863475287 6,5,5   24      2       96
35:     58.941502773372 6,6,4   24      2       96
36:     65.296777112432 6,6,6   8       2       32

Realspace Spacings

Since $q=2\pi /d$, the realspace spacing of planes is:

${\begin{alignedat}{2}\mathbf {q} _{hkl}&=(2\pi h)\mathbf {u} +(2\pi k)\mathbf {v} +(2\pi l)\mathbf {w} \\&=(2\pi h){\begin{bmatrix}{\frac {1}{a}}\\{\frac {1}{{\sqrt {3}}a}}\\0\end{bmatrix}}+(2\pi k){\begin{bmatrix}0\\{\frac {2}{{\sqrt {3}}b}}\\0\end{bmatrix}}+(2\pi l){\begin{bmatrix}0\\0\\{\frac {1}{c}}\end{bmatrix}}\\&={\begin{bmatrix}{\frac {2\pi h}{a}}\\{\frac {2\pi h}{{\sqrt {3}}a}}+{\frac {4\pi k}{{\sqrt {3}}b}}\\{\frac {2\pi l}{c}}\end{bmatrix}}\\&={\begin{bmatrix}{\frac {2\pi h}{a}}\\{\frac {2\pi (h+2k)}{{\sqrt {3}}a}}\\{\frac {2\pi l}{c}}\end{bmatrix}}\end{alignedat}}$

Examples

Elemental

3. Lithium (Li) (a = 3.509 Å)

11. Sodium (Na) (a = 4.291 Å)

19. Potassium( K) (a = 5.247 Å) (at 78 K)

23. Vanadium (V) (a = 3.024 Å)

24. Chromium (Cr) (a = 2.884 Å)

26. Iron (Fe) (a = 2.866 Å)

37. Rubidium (Rb) (a = 5.605 Å) (at 78 K)

41. Niobium (Nb) (a = 3.300 Å)

42. Molybdenum (Mo) (a = 3.147 Å)

55. Caesium (Cs) (a = 6.067 Å) (at 78 K)

56. Barium (Ba) (a = 5.025 Å)

63. Europium (Eu) (a = 4.606 Å)

73. Tantalum (Ta) (a = 3.306 Å)

74. Tungsten (W) (a = 3.165 Å)

Atomic

• TBD

Nano

• TBD

Body-centered Two-particle

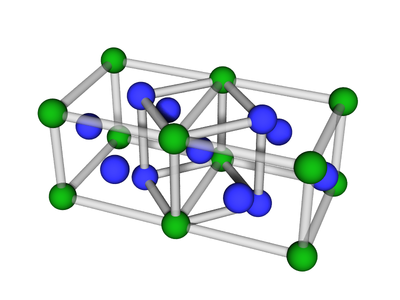
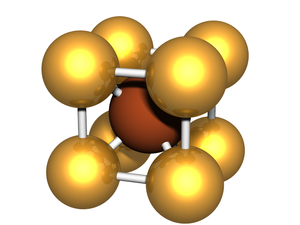
A lattice where the unit cell has two distinct atoms/particles, arranged with one at the center of the simple cubic lattice defined by the other, has simple cubic symmetry. This lattice is often called CsCl.

Symmetry

• Crystal Family: Cubic
• Crystal System: Cubic
• Bravais Lattice: P (pcc)
• Crystal class: Hexoctahedral
• Point Group: m3m
• Space Group: Pm3m
• Particles per unit cell: $n=2$ (distinct)
• Volume of unit cell: $V_{d}=a^{3}$
• Dimensionality: $d=3$
• Projected d-dimensional volume: $v_{d}=a^{3}$
• Solid angle: $\Omega _{d}=4\pi$
• Nearest-neighbor distance: $d_{nn}={\sqrt {3}}a/2$

Examples

Atomics

• Cesium chloride (CsCl) (a = 4.11 Å)

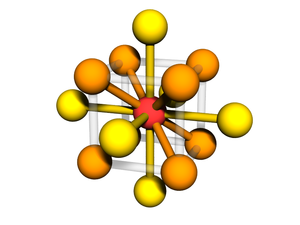
Body-centered with Edges and Faces

The BCC lattice, where a second particle type occupies positions along edges and faces. The symmetry is the same as the canonical BCC. (The particles at the face position are effective 'edge' particles with respect to the center particle...)

Particle Positions

There are 27 positions, with 8 particles in the unit cell

Particle A

These are the usual BCC positions. There are 9 positions. In total there are 2 particles in the unit cell:

• $8\,\mathrm {corners} \,\times \,{\frac {1}{8}}=1$
  • $\left(0,0,0\right),(0,0,1),(0,1,0),(1,0,0),(0,1,1),(1,0,1),(1,1,0),(1,1,1)$
• $1\,\mathrm {center} \,\times \,1=1$
  • $\left({\frac {1}{2}},{\frac {1}{2}},{\frac {1}{2}}\right)$

Particle B

There are 18 positions, with 6 particles in the unit cell.

• $6\,\mathrm {faces} \,\times \,{\frac {1}{2}}=3$
  • $\left(0,{\frac {1}{2}},{\frac {1}{2}}\right),\left({\frac {1}{2}},0,{\frac {1}{2}}\right),\left({\frac {1}{2}},{\frac {1}{2}},0\right),\left(1,{\frac {1}{2}},{\frac {1}{2}}\right),\left({\frac {1}{2}},1,{\frac {1}{2}}\right),\left({\frac {1}{2}},{\frac {1}{2}},1\right)$
• $12\,\mathrm {edges} \,\times \,{\frac {1}{4}}=3$
  • $\left({\frac {1}{2}},0,0\right),\left(0,{\frac {1}{2}},0\right),\left(0,0,{\frac {1}{2}}\right)$
  • $\left(1,0,{\frac {1}{2}}\right),\left(1,1,{\frac {1}{2}}\right),\left(0,1,{\frac {1}{2}}\right),\left({\frac {1}{2}},1,0\right),\left(1,{\frac {1}{2}},0\right),\left({\frac {1}{2}},0,1\right),\left(0,{\frac {1}{2}},1\right),\left(1,{\frac {1}{2}},1\right),\left({\frac {1}{2}},1,1\right)$

See Also

• Wikipedia: Cubic crystal system