Neutron scattering lengths

For neutrons, the b_i in the above equation are the neutron scattering lengths for the atoms in question.

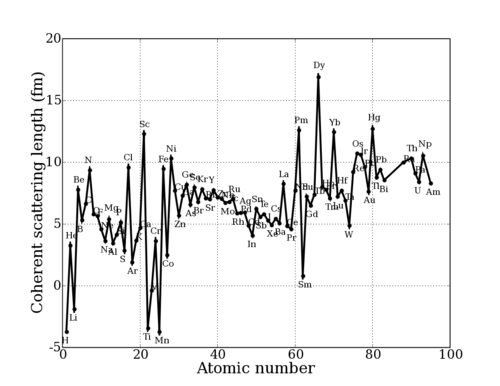
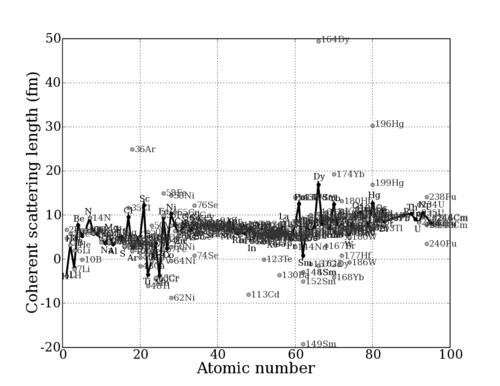
This value depends sensitively on the details of the nuclear interaction, and thus on the nuclear properties (spin, energy levels, etc.) of any particular nuclide (isotopic nucleus). Thus, the scattering length varies seemingly irregularly throughout the periodic table. This can be seen in the graphs below.

Neutron scattering length for Elements

Neutron scattering length for Isotopes

Scattering Length Density

The neutron scattering lengths directly control the Scattering Length Density (SLD) of materials; i.e. the strength of neutron scattering from a given material. The wide variation of SLD for materials makes neutrons a uniquely powerful structural probe. On the one hand, one can vary the contrast condition simply by changing one isotope for another. For example, selective deuteration (of a material or a solvent) can be used to enhance a particular contrast, or to 'contrast match' a particular structure, thereby making it invisible to the neutron beam (and highlighting other structures). One can also attempt to, e.g., substitute one ion for an isovalent ion with a radically different SLD; or to perform the same experiment twice, with the substrate (or even just a layer in the substrate) swapped. The different contrast conditions allow for more robust data fitting (since a solution consistent with both datasets can resolve fitting ambiguities).

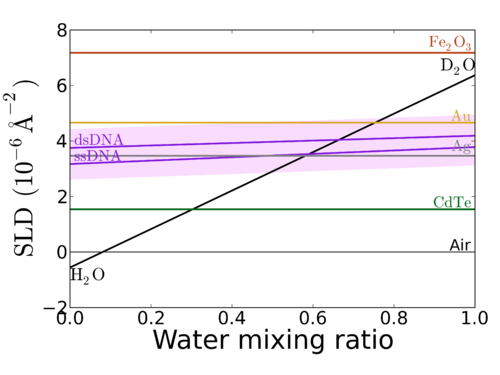
A common 'trick' in neutron experiments is to vary the ratio of H₂O to D₂O in the solvent; which allows one to vary the ambient SLD across a very wide range:

Origin of the scattering lengths

The following description is adapted from [www.ncnr.nist.gov/programs/sans/pdf/polymer_tut.pdf Boualem Hammouda's (NCNR) SANS tutorial].

Consider a neutron of energy $E_{i}$ interacting with a nucleus, which exhibits an attractive square well of $-V_{0}$; where $V_{0}\gg E_{i}$. The Schrödinger equation is:

$\left[\right]=E\psi$

See Also

• Neutron data booklet: Tabulates fundamental properties of neutron interactions with matter; also provides useful equations.
• NIST: Periodic table of neutron scattering lengths and cross sections
• SLD calculator: NIST Center for Neutron Research calculator for predicting the neutron Scattering Length Density (SLD) for materials.