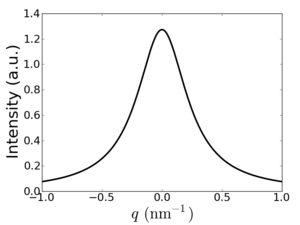
Peak shape
The peak width observed in x-ray scattering can be related to the grain size of the ordered structure giving rise to the scattering peak. More generally, the peak shape also encodes information about the sample order. Thus, peak shape analysis can be used to extract higher-order information.
Note also that instrumental resolution contributes to peak width, and also to peak shape. Scattering peaks are thus sometimes fit using functions that include two contributes (e.g. a Gaussian, representing material grain size, plus a Lorentzian, representing instrumental resolution).
Contents
Generalized Peak Shape
A generalized peak shape can be computed using:
Where , describes the peak width, and describes the peak shape. The parameter is a ratio of gamma functions:
The limiting cases for peak shape are:
Thus the parameter allows one to vary continuously between a Lorentzian peak shape and a Gaussian peak shape. Note that for Lorentzian, describes the full-width at half-maximum (FWHM):
The Gaussian form can be written a few different ways:
where the width is described by:
And note that 2.35482004503...
Source
- Scattering Curves of Ordered Mesoscopic Materials S. Förster, A. Timmann, M. Konrad, C. Schellbach, A. Meyer, S.S. Funari, P. Mulvaney, R. Knott, J. Phys. Chem. B, 2005, 109 (4), pp 1347–1360 DOI: 10.1021/jp0467494
Literature Examples
Warren/Averbach paracrystal
- B. E. Warren, X-RAY STUDIES OF DEFORMED METALS Progress in Metal Physics 1959, 8, 174-202 doi: 10.1016/0502-8205(59)90015-2
- B.E. Warren, B.L. Averbach, The Effect of Cold‐Work Distortion on X‐Ray Patterns J. Appl. Phys. 1950, 21, 595 doi: 10.1063/1.1699713
- B.E. Warren, B.L. Averbach, The Separation of Cold‐Work Distortion and Particle Size Broadening in X‐Ray Patterns J. Appl. Phys. 1952, 23, 497 doi: 10.1063/1.1702234
- B. Crist and J.B. Cohen Fourier Analysis of Polymer X-Ray Diffraction Patterns J. Poly. Sci: Poly. Phys. 1979, 17 (6), 1001-1010 doi: 10.1002/pol.1979.180170609
- T.J. Prosa , J. Moulton , A.J. Heeger, and M.J. Winokur, Diffraction Line-Shape Analysis of Poly(3-dodecylthiophene): A Study of Layer Disorder through the Liquid Crystalline Polymer Transition Macromolecules 1999, 32 (12), 4000-4009 doi: 10.1021/ma981059h
- Rodrigo Noriega, Jonathan Rivnay, Koen Vandewal, Felix P. V. Koch, Natalie Stingelin, Paul Smith, Michael F. Toney & Alberto Salleo, A general relationship between disorder, aggregation and charge transport in conjugated polymers Nature Materials 2013, 12, 1038-1044 doi: 10.1038/nmat3722; see also Supplementary Information.
- Rodrigo Noriega, Jonatahan Rivnay, Alberto Salleo, Michael Toney Warren Averbach analysis of XRD peak shapes: Measuring disorder in soft organic materials
Williamson/Hall
- G.K. Williamson, W.H. Hall, X-ray line broadening from filed aluminium and wolfram Acta Metallurgica 1953, 1 (1), 22-31.
Grain Size Distribution
- E.F. Bertaut Raies de Debye-Scherrer et repartition des dimensions des domaines de Bragg dans les poudres polycristallines Acta Cryst. 1950, 3, 14-18 doi: 10.1107/S0365110X50000045
- S. Rao and C. R. Houska, X-ray particle-size broadening Acta Cryst. 1986', A42, 6-13 doi: 10.1107/S0108767386099981
- J. I. Langford, D. Louër and P. Scardi, Effect of a crystallite size distribution on X-ray diffraction line profiles and whole-powder-pattern fitting doi: 10.1107/S002188980000460X
- T. Ungár, J. Gubicza, G. Ribárik and A. Borbély, Crystallite size distribution and dislocation structure determined by diffraction profile analysis: principles and practical application to cubic and hexagonal crystals J. Appl. Cryst. 2001, 34, 298-310 doi: 10.1107/S0021889801003715
Fourier Analysis
- C.E. Kril and R. Birringer, Estimating grain-size distributions in nanocrystalline materials from X-ray diffraction profile analysis Philosophical Magazine A 1998, 77 (3), 621-640 doi: 10.1080/01418619808224072
- J. Gubicza, J. Szépvölgyi, I. Mohai, L. Zsoldos, T Ungár, Particle size distribution and dislocation density determined by high resolution X-ray diffraction in nanocrystalline silicon nitride powders Materials Science and Engineering: A 2000, 280 (3), 263-269 doi: 10.1016/S0921-5093(99)00702-9
Maximum Entropy
- N. Armstrong and W. Kalceff, A maximum entropy method for determining column-length distributions from size-broadened X-ray diffraction profiles J. Appl. Cryst. 1999, 32, 600-613 doi: 10.1107/S0021889899000692
Other
- F.W. Jones, The Measurement of Particle Size by the X-Ray Method Proceedings of the Royal Society A 1938, 166 (924) 16-43 doi: 10.1098/rspa.1938.0079
- R.A. Young and D.B. Wiles, Profile Shape Functions in Rietveld Refinements J. Appl. Cryst. 1982, 15, 430-438 doi: 10.1107/S002188988201231X
- R.J. Hill and C.J. Howard, Peak shape variation in fixed-wavelength neutron powder diffraction and its effect on structural parameters obtained by Rietveld analysis J. Appl. Cryst. 1985, 18, 173-180 doi: 10.1107/S0021889885010068
- D. Louer and J.I. Langford Peak Shape and Resolution in Conventional Diffractometry with Monochromatic X-rays J. Appl. Cryst. 1988, 21, 430-437.
- Gy. Zilahi, T. Ungár and G. Tichy A common theory of line broadening and rocking curves J. Appl. Cryst. 2015, 48. doi: 10.1107/S1600576715001466
See Also
- Estimating Crystallite Size Using XRD, Scott A. Speakman, MIT.
- Scherrer grain size analysis: Converting the peak width into a measure of the structural coherence length (grain size)
- Ring graininess: Estimating grain size using the non-uniformity of the scattering ring. (Can be used to compute grain sizes even when the grains are so large that the peak width is instrumental-limited.)
![{\displaystyle {\begin{alignedat}{2}L_{hkl}(q)&={\frac {2}{\pi \delta }}\prod _{n=0}^{\infty }{\left(1+{\frac {\gamma _{\nu }^{2}}{(n+\nu /2)^{2}}}{\frac {4q_{s}^{2}}{\pi ^{2}\delta ^{2}}}\right)^{-1}}\\&={\frac {2}{\pi \delta }}\left|{\frac {\Gamma \left[\nu /2+i\gamma _{\nu }(4q_{s}^{2}/\pi ^{2}\delta ^{2})^{2}\right]}{\Gamma \left[\nu /2\right]}}\right|^{2}\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8af787457104932059fe6386c7dba660b2748f5)




![{\displaystyle \gamma _{\nu }={\sqrt {\pi }}{\frac {\Gamma \left[(\nu +1)/2\right]}{\Gamma \left[\nu +/2\right]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8b76d4ccc14be3620d12982767eae2d372c3e96)
![{\displaystyle L_{hkl}(q_{s})=\left\{{\begin{array}{c l l}{\frac {\delta /2\pi }{q_{s}^{2}+(\delta /2)^{2}}}&\mathrm {for} \,\,\nu \to 0&\mathrm {(Lorentzian)} \\{\frac {2}{\pi \delta }}\exp \left[-{\frac {4q_{s}^{2}}{\pi \delta ^{2}}}\right]&\mathrm {for} \,\,\nu \to \infty &\mathrm {(Gaussian)} \\\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e553e875538b6ebcad8d4d81fadbc60564cdb76c)

![{\displaystyle {\begin{alignedat}{2}L_{hkl,\mathrm {gauss} }(q_{s})&={\frac {2}{\pi \delta }}\exp \left[-{\frac {4q_{s}^{2}}{\pi \delta ^{2}}}\right]\\&={\frac {1}{{\sqrt {2\pi }}\sigma }}\exp \left[-{\frac {q_{s}^{2}}{2\sigma ^{2}}}\right]\\&={\sqrt {\frac {\ln {2}}{\pi }}}{\frac {1}{\mathrm {fwhm} }}\exp \left[-{\frac {4\ln {2}q_{s}^{2}}{\mathrm {fwhm} ^{2}}}\right]\\\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a5ddd434d0b8d4241df2c2d705c4066829bb88c)



