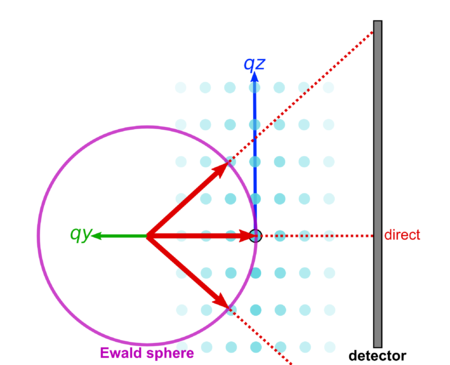
Ewald sphere
The Ewald sphere is the surface, in reciprocal-space, that all experimentally-observed scattering arises from. (Strictly, only the elastic scattering comes from the Ewald sphere; inelastic scattering is so-called 'off-shell'.) A peak observed on the detector indicates that a reciprocal-space peak is intersecting with the Ewald sphere.
Although the Ewald sphere may seem like an abstract concept, it is simply the geometric representation of the scattering equation (i.e. it is the surface that satisfies the scattering condition).
Contents
Mathematics
In TSAXS of an isotropic sample, we only probe the magnitude (not direction) of the momentum transfer:
Where is the full scattering angle. In GISAXS, we must take into account the vector components:
Where is the incident angle (the grazing angle of the beam with respect to the substrate plane), is the out-of-plane scattering angle (with respect to the substrate plane), and is the full in-plane scattering angle.
Derivation
Definitions
Consider reciprocal-space in the incident beam coordinate system: . The incident beam is the vector , where:
where is, of course, the wavelength of the incident beam. An elastic scattering event has an outgoing momentum () of the same magnitude as the incident radiation (i.e. ). Consider a momentum vector, and resultant momentum transfer, , of:
The magnitude of the momentum transfer is thus:
where is the full scattering angle. The Ewald sphere is centered about the point and thus has the equation:
TSAXS
In conventional SAXS, the signal of interest is isotropic: i.e. we only care about , and not the individual (directional) components . In such a case we use the form of q derived above:
In the more general case of probing an anisotropic material (e.g. CD-SAXS), one must take into account the full q-vector, and in particular the relative orientation of the incident beam and the sample: i.e. the relative orientation of the Ewald sphere and the reciprocal-space.
GISAXS
Now let us assume that the incident beam strikes a thin film mounted to a substrate. The incident beam is in the grazing-incidence geometry (e.g. GISAXS, and we denote the angle between the incident beam and the film surface as . The reciprocal-space of the sample is thus rotated by with respect to the beam reciprocal-space coordinates. We convert to the sample's reciprocal coordinate space; still denoted by . The equation of the Ewald sphere becomes (the center of the sphere is at ):
Reflectivity
Consider for a moment that the q-vector is confined to the plane:
Obviously the specular condition is when , in which case one obtains:
That is, reflectivity is inherently only probing the out-of-plane () component:
Out-of-plane scattering only
TBD
General form
TBD
Literature
Conceptual Understanding of Ewald sphere
- Simulating X-ray diffraction of textured films D. W. Breiby, O. Bunk, J. W. Andreasen, H. T. Lemke and M. M. Nielsen J. Appl. Cryst. 2008, 41, 262-271. doi: 10.1107/S0021889808001064
- Quantification of Thin Film Crystallographic Orientation Using X-ray Diffraction with an Area Detector Jessy L. Baker, Leslie H. Jimison, Stefan Mannsfeld, Steven Volkman, Shong Yin, Vivek Subramanian, Alberto Salleo, A. Paul Alivisatos and Michael F. Toney Langmuir 2010, 26 (11), 9146-9151. doi: 10.1021/la904840q
Equations of GISAXS Geometry
- gisaxs.de: Brief introduction to the theory of GISAXS.
- IsGISAXS Manual: Provides a complete description (including equations) of the GISAXS theory required to model data.
- Probing surface and interface morphology with Grazing Incidence Small Angle X-Ray Scattering Gilles Renaud, Rémi Lazzari, Frédéric Leroy, Surface Science Reports 2009, 64 (8), 255-380. doi: 10.1016/j.surfrep.2009.07.002
- A Basic Introduction to Grazing Incidence Small-Angle X-Ray Scattering P. Müller-Buschbaum DOI 10.1007/978-3-540-95968-7 (Chapter 3 in Applications of Synchrotron Light to Scattering and Diffraction in Materials and Life Sciences)



![{\displaystyle {\begin{alignedat}{2}q_{x}&={\frac {2\pi }{\lambda }}\cos(\alpha _{f})\sin(2\theta _{f})\\q_{y}&={\frac {2\pi }{\lambda }}\left[\cos(\alpha _{f})\cos(2\theta _{f})-\cos(\alpha _{i})\right]\\q_{z}&={\frac {2\pi }{\lambda }}\left[\sin(\alpha _{f})+\sin(\alpha _{i})\right]\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27547a095e95a18446c4faf183875dde8280f221)











![{\displaystyle {\begin{alignedat}{2}q&=|\mathbf {q} |\\&={\sqrt {[2k\sin ^{2}(\theta _{s}))]^{2}+[2k\sin(\theta _{s})\cos(\theta _{s})]^{2}}}\\&={\sqrt {4k^{2}[\sin ^{4}(\theta _{s})+\sin ^{2}(\theta _{s})\cos ^{2}(\theta _{s})]}}\\&=2k{\sqrt {\sin ^{4}(\theta _{s})+\sin ^{2}(\theta _{s})\cos ^{2}(\theta _{s})}}\\&=2k{\sqrt {\sin ^{2}(\theta _{s})}}\\&=2k\sin(\theta _{s})\\&={\frac {4\pi }{\lambda }}\sin(\theta _{s})\\\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ca11ba030ff565330aa97dd59efe9842d76c8dc)














