Sample orientation
For isotropic materials, the orientation of the sample with respect to the beam does not matter. However, for any sample that is anisotropic the sample orientation will strongly influence the scattering pattern. This effect is relevant for any intrinsically anisotropic material, including crystals and aligned bulk materials (liquid crystals, stretched polymers, etc.). Any material which has broken symmetry will also be anisotropic: e.g. a thin film is inherently different along the film normal than in the in-plane direction, and thus is not truly anisotropic.
Anisotropy in the sample is reflected in anisotropy in the reciprocal-space. Thus, the scattering pattern one observes on the detector will depend on the orientation of the sample with respect to the beam.
Reciprocal-space
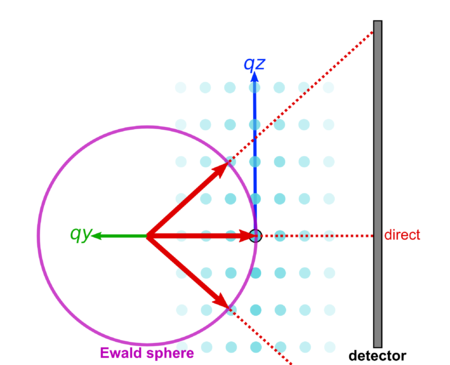
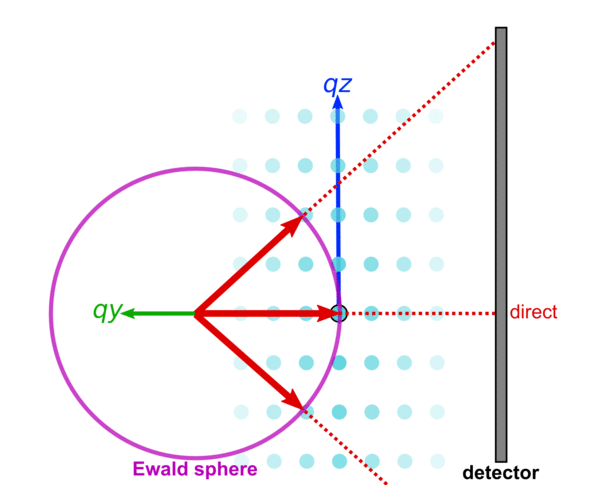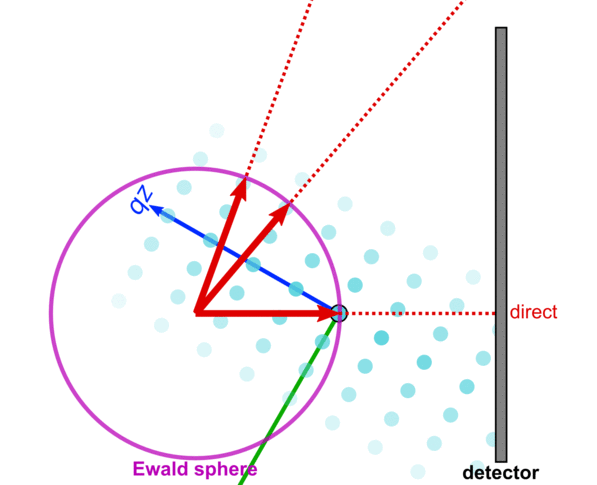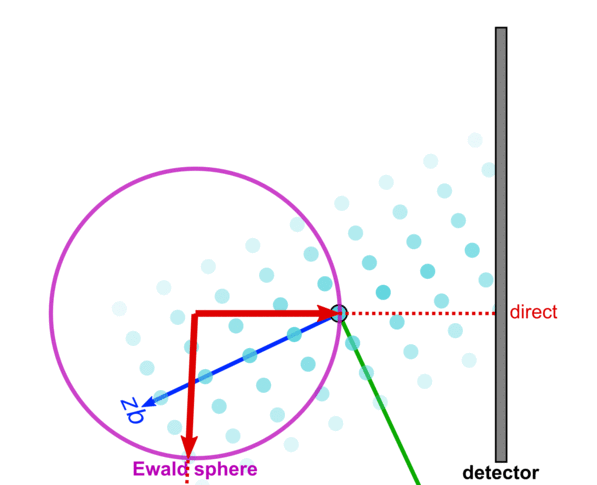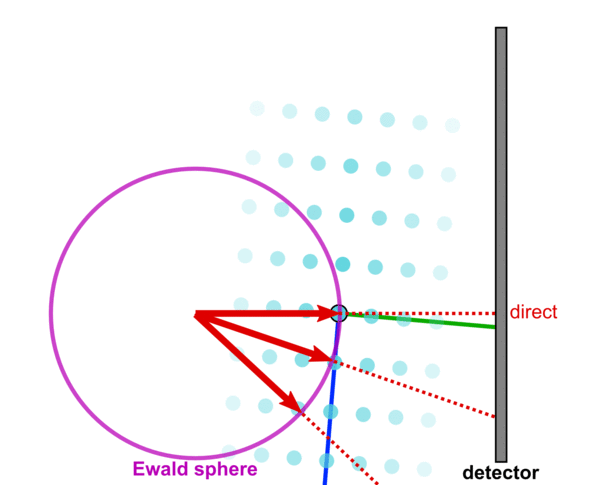
This is best understood in terms of reciprocal-space. Recall that the signal observed on the detector arises from the intersection of the Ewald sphere with the reciprocal lattice.
If we reorient the sample, we bring a different set of reciprocal-space peaks into the intersection condition. That is, we bring a different set of crystal planes in the sample into the 'Bragg condition' wherein they give rise to a diffraction peak.
Reconstruction
In order to map out the entire reciprocal-space, one can completely rotate the sample, and collection a wide set of images. Adding these images together enables the full 3D reciprocal-space to be reconstructed.
See Also
- Rocking scan
- Reciprocal-space mapping
- Example:P3HT orientation analysis
- L. Urzhumtseva and A. Urzhumtsev py_convrot: rotation conventions, to understand and to apply J. Appl. Cryst. 2019 doi: 10.1107/S1600576719007313