Scattering Length Density
The Scattering Length Density (SLD, sometimes denoted Nb) is a measure of the scattering power of a material. It increases with the physical density (how tightly packed the scattering entities are), as well as the intrinsic scattering power of the 'scattering entities'. For x-rays, the scattering arises from the electron density, whereas for neutrons, the scattering arises from the nuclear scattering lengths.
Contents
Calculating
SLD can be computed from the scattering lengths and material densities. Specifically:
where we sum the scattering length contributions (bi) from the N atoms within the unit cell, and divide by the volume, Vm of this 'unit cell'. Note that the 'unit cell' need not be a crystallographic unit cell: it is simply a representative volume of the material in question: the atoms within it may be arranged randomly (e.g. amorphous material) or in a crystalline way. For instance for a single molecule, Vm is simply the molecular volume, and the sum includes all the atoms in the molecule. In general we don't know what the appropriate 'molecular volume' should be, but we can compute it from the known bulk density of the material () and the molecular weight (M):
Where Na is the Avogadro constant. Thus:
where Mi is the atomic molar mass for each element. Note that the above sum is over every atom in the representative volume (i.e. a particular atom repeated twice should be added twice). The equation can be recast in terms of weighting factors (stoichiometric numbers in a chemical formula, or concentrations in a mixture) to yield:
Neutron scattering lengths
For neutrons, the bi in the above equation are the neutron scattering lengths for the atoms in question. This value depends on the strength of the interaction between a neutron and a given nucleus. It is in general not easy to predict this quantity theoretically; instead experiments are performed to tabulate the scattering lengths. Refer to the neutron data booklet (starting on page 1.1-8) for tables of bi for known isotopes.
X-ray scattering lengths
For x-rays, the scattering arises from the interaction between the incident wave and the electron clouds of the atoms in the material. Thus, the scattering power scales with electron density in the material (with corrections for additional effects, such as resonant scattering, a.k.a. absorption lines). In practice, one can look up tabulated values of the atomic scattering factor for the atom in question. From this, one can compute the scattering length using:
Where f1 is the real part of the atomic scattering factor, e is the charge of the electron (1.602176565×10−19 coulombs), ε0 is the permittivity of free space (8.854187817x10−12 F/m), me is the mass of the electron (9.10938215×10−31 kg), and c is the speed of light (299,792,458 m/s).
The prefactor to f1 is simply the classical electron radius (re), and has the value 2.8179403x10−15 m.
Converting
SLD is typically used in the neutron scattering community, but is less common in x-ray scattering. The SLD can be converted to the x-ray refractive index using:
Elemental dependence
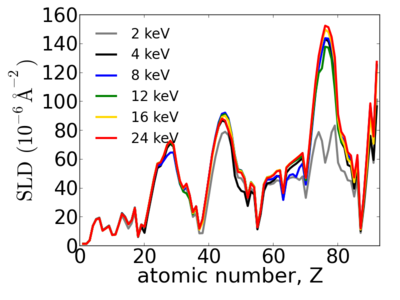
Notice that the structure of the periodic table is reflected in the SLD.
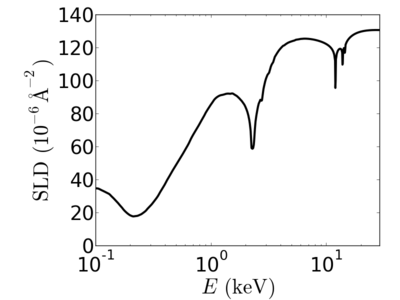
Energy dependence
Examples
silicon
gold
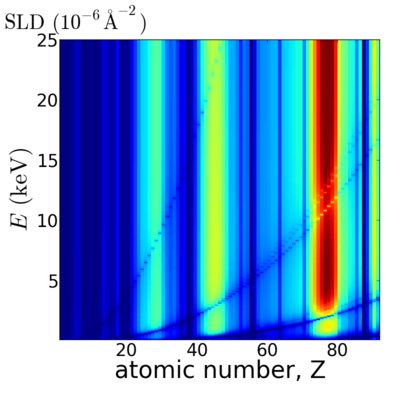
Elemental/Energy dependence
See Also
- Critical angle
- SLD calculator: NIST Center for Neutron Research calculator for predicting SLD.