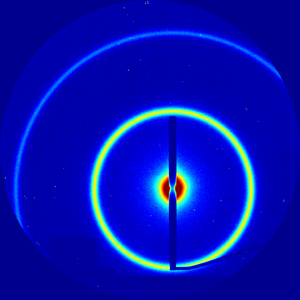
Scattering features
Scattering experiments (x-ray or neutron) generates images which can be thought of as the Fourier transform of the material's realspace structure. I.e. the image is a slice through a conceptual 3D reciprocal-space. Although a scattering pattern can be arbitrarily complex, there are usually various features that can be analyzed separately, and from which one can learn much about a sample's structure. In particular, samples with well-defined structural order give rise to distinct scattering features, such as sharp rings or even distinct spots on the area detector image.
Contents
Diffuse Scattering
Many samples will exhibit diffuse scattering: scattering intensity over a broad range of angles, without a distinct peak or maximum. This kind of scattering usually comes from disorder within the sample. For instance, low-q diffuse scattering can come from nanoscale or microscale porosity, or from surface roughness in GISAXS. High-q diffuse scattering can arise from the defects in atomic lattices (and from the thermal motion of atoms in a lattice). Although one can generally assign diffuse scattering to some kind of disorder, it is difficult to make an unambiguous link, because there are many effects that can generate diffuse scattering.
Spots
A sharp spot on a 2D detector is typically a Bragg peak: i.e. diffraction at a well-defined angle due to a realspace lattice. An array of sharp spots typically indicates that the sample is a single-crystal (or at least oriented; e.g. in-plane powder).
Rings
A ring typically indicates an isotropic material generating Bragg peak that is spread orientationally. Thus, the sample is poly-crystalline, with crystallites at every possible orientation, but with a well-defined unit cell giving rise to diffraction spots. These spots are smeared orientationally, giving rise to a set of distinct rings. The ring position can be converted into a realspace repeat distance (e.g. to determine a packing distance). With enough rings, one can determine the unit cell symmetry (i.e. it becomes a powder diffraction experiment, from which one can fit the crystallographic symmetry).
Broad Rings
A very broad ring (or halo) indicates a poorly ordered system, with very small grain sizes. For instance, the sample may be poly-crystalline, with very small grain sizes. Alternatively, the material may be essentially amorphous, with the ring indicating a preferred local packing distance, but no long-range coherent order.
Speckled Rings
A sharp ring that is speckled indicates that the material is poly-crystalline, but the grains are exceptionally large. As such, only a small number of grains within the scattering volume satisfy the Bragg condition, leading to just a small number of spots. A sharp, speckled ring thus indicates a highly ordered system, with large grains. (The ring graininess can be quantified to measure grain size.)

Bragg Rods
TBD
Yoneda Streak
TBD
Speckles
TBD