Difference between revisions of "Wave packet"
KevinYager (talk | contribs) (→Propagation and Interaction) |
KevinYager (talk | contribs) (→Propagation and Interaction) |
||
| Line 14: | Line 14: | ||
==Wave-particle duality== | ==Wave-particle duality== | ||
In the context of [[quantum mechanics]], particles can be thought of as wave-packets. That is, quantum particles are neither ideal point-like particles, nor ideal plane-waves. They are instead intermediate objects, which are certainly wave-like (e.g. can undergo interference), but also somewhat localized. The classical concepts of 'particle' (perfectly localized; mathematically a delta-function), and 'wave' (oscillation with a single well-defined wavelength, spread infinitely over all space) can be viewed as limited cases of the general wave-packet. These limiting cases are only conceptual: in reality neither can exist. | In the context of [[quantum mechanics]], particles can be thought of as wave-packets. That is, quantum particles are neither ideal point-like particles, nor ideal plane-waves. They are instead intermediate objects, which are certainly wave-like (e.g. can undergo interference), but also somewhat localized. The classical concepts of 'particle' (perfectly localized; mathematically a delta-function), and 'wave' (oscillation with a single well-defined wavelength, spread infinitely over all space) can be viewed as limited cases of the general wave-packet. These limiting cases are only conceptual: in reality neither can exist. | ||
| + | |||
| + | ==Components== | ||
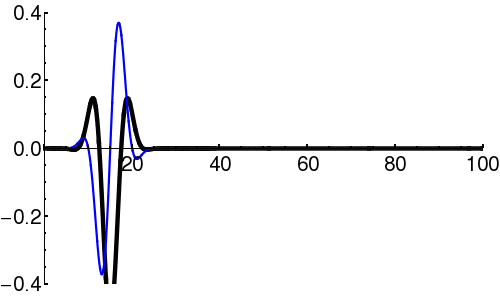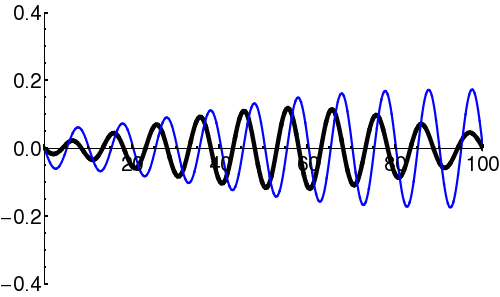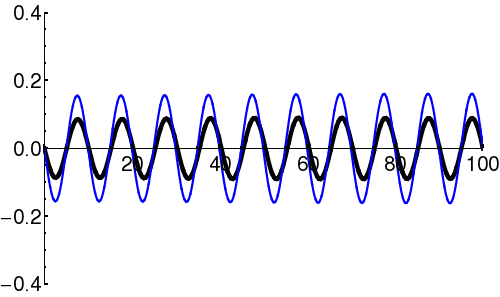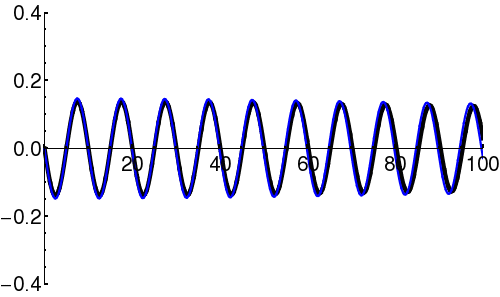
| + | In [[quantum mechanics]], the wave-packet necessarily has both real and imaginary components. | ||
| + | {| | ||
| + | | [[Image:Free packet1.png|300px|thumb|Components of the wavefunction (<math>\scriptstyle \psi(x) </math>) describing a propagating wave-packet. The black line is the real part, and the blue line is the imaginary part.]] | ||
| + | |- | ||
| + | | [[Image:Free packet2.png|300px|thumb|Square of the wavefunction (<math>\scriptstyle | \psi(x) |^2 </math>) for a propagating wave-packet. This describes the spatial spread of the function.]] | ||
| + | |} | ||
| + | |||
==Propagation and Interaction== | ==Propagation and Interaction== | ||
Latest revision as of 09:52, 3 November 2014
A wave packet is a localized wavelike perturbation, which appears frequently in quantum descriptions of particles. For instance, incident x-rays during scattering experiments can be thought of as wave-packets.
.gif)
Contents
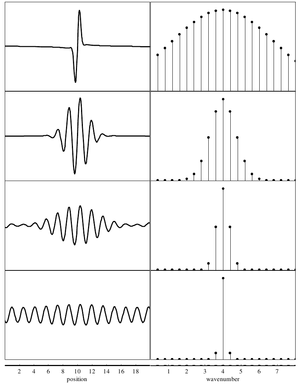
Position-momentum tradeoff
The wave-packet can be described as a wavefunction in either position-space or momentum-space:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x) = \frac{1}{\sqrt{2 \pi}} \int \tilde{\psi}(k) e^{i k x } \mathrm{d}k }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{\psi}(k) = \frac{1}{\sqrt{2 \pi}} \int {\psi}(x) e^{-i k x } \mathrm{d}x }
Note that these two descriptions are Fourier transforms of one another. Thus, there is an inherent tradeoff between the 'spread' of a wave-packet in position-space vs. momentum-space.
Wave-particle duality
In the context of quantum mechanics, particles can be thought of as wave-packets. That is, quantum particles are neither ideal point-like particles, nor ideal plane-waves. They are instead intermediate objects, which are certainly wave-like (e.g. can undergo interference), but also somewhat localized. The classical concepts of 'particle' (perfectly localized; mathematically a delta-function), and 'wave' (oscillation with a single well-defined wavelength, spread infinitely over all space) can be viewed as limited cases of the general wave-packet. These limiting cases are only conceptual: in reality neither can exist.
Components
In quantum mechanics, the wave-packet necessarily has both real and imaginary components.
 Components of the wavefunction (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \psi(x) }
) describing a propagating wave-packet. The black line is the real part, and the blue line is the imaginary part. |
 Square of the wavefunction (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle | \psi(x) |^2 }
) for a propagating wave-packet. This describes the spatial spread of the function. |
Propagation and Interaction
Wave-packets can propagate, frequently with dispersion (which induces spatial spread of the envelope). Wave-packets can interact with barriers (defined by, e.g., some potential function), and interfere with themselves.
 Components of the wavefunction (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \psi(x) }
) describing a wave-packet bouncing inside a box-like potential. The black line is the real part, and the blue line is the imaginary part. |
 Square of the wavefunction (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle | \psi(x) |^2 }
) for a wave-packet bouncing inside a box-like potential. |
