Circular orientation distribution function
In assessing the orientation of aligned materials, one can use the orientation order parameter to quantify order. Another possibility is to fit scattering data using an equation that has 'circular wrapping' (i.e. periodic along Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle 2 \pi} ).
Contents
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \eta } function
Ruland et al. present such an equation:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I (\chi) = \frac{1 - \eta^2}{(1+\eta)^2 - 4 \eta \cos^2 \chi} }
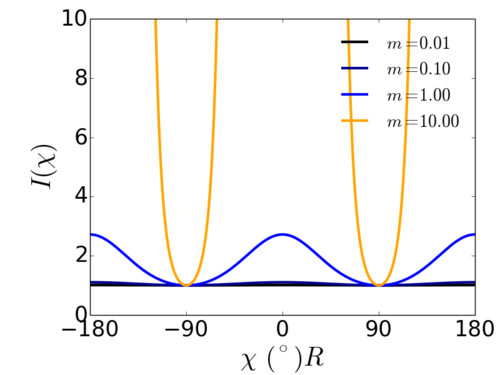
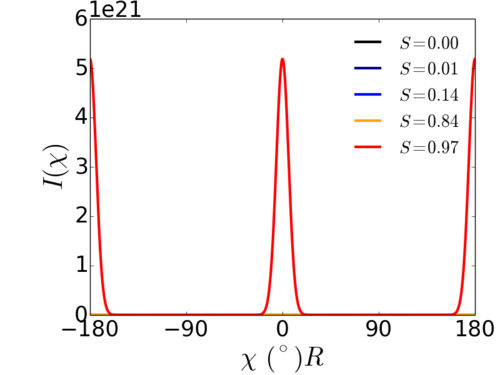
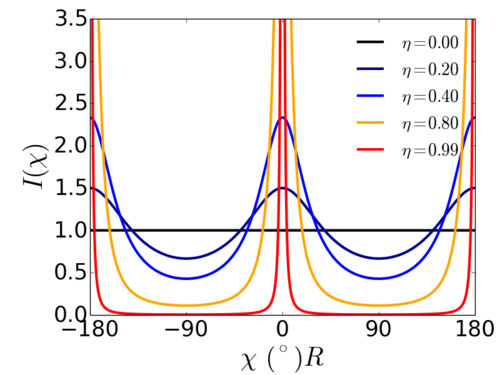
Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \chi } is the angle along the arc of the scattering ring/feature. The single fit parameter (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \eta } ) is convenient in that it behaves in a similar way to an order parameter: a value close to 1.0 indicates strong alignment, while progressively smaller values indicate lesser alignment. For a random sample, the scattering is isotropic and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \eta = 0} .
Normalized
The function normalized so that the maximum is always at 1 would be:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_{\mathrm{norm}} (\chi) = \frac{(1+\eta)^2 - 4 \eta}{(1+\eta)^2 - 4 \eta \cos^2 \chi} }
References
- Ruland, W.; Tompa, H., The Effect of Preferred Orientation on the Intensity Distribution of (Hk) Interferences. Acta Crystallographica Section A 1968, 24, 93-99. 10.1107/S0567739468000112
- Ruland, W.; Smarsly, B., Saxs of Self-Assembled Oriented Lamellar Nanocomposite Films: An Advanced Method of Evaluation. J. Appl. Crystallogr. 2004, 37, 575-584. doi: 10.1107/S0021889804011288
- Kevin G. Yager, Christopher Forrey, Gurpreet Singh, Sushil K. Satija, Kirt A. Page, Derek L. Patton, Jack F. Douglas, Ronald L. Jones and Alamgir Karim Thermally-induced transition of lamellae orientation in block-copolymer films on ‘neutral’ nanoparticle-coated substrates Soft Matter 2015 doi: 10.1039/C5SM00896D
Maier-Saupe distribution parameter
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(\chi) = \frac{1}{c} \exp \left [ m \cos ^2 \chi \right ] }
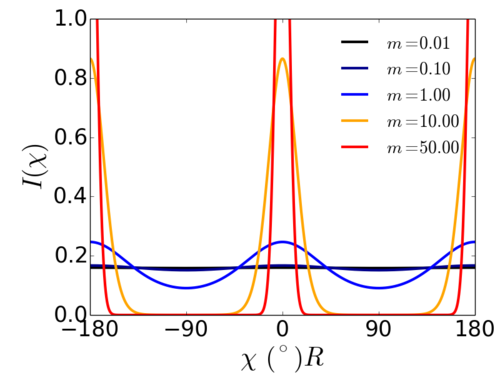
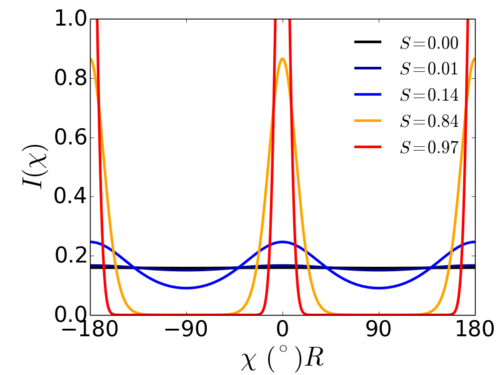
Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle m} is a parameter that can be related to the order parameter Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle S} ; specifically Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle m =0 } is for an isotropic distribution (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle S = 0} ), while Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle m \to \infty} is for a well-aligned system (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle S \to 1} ).
The parameter c can be used to normalize:
