Form Factor:Sphere

This page provides the equations for calculating the form factor of a sphere (including derivations).

Equations

For spheres of radius R (volume Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V_{sphere}=4\pi R^3/3} ):

Form Factor Amplitude

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F_{sphere}(q) = \left\{ \begin{array}{c l} 3 \Delta\rho V_{sphere} \frac{ \sin(qR)-qR \cos(qR) }{ (qR)^3 } & \mathrm{when} \,\, q\neq0\\ \Delta\rho V_{sphere} & \mathrm{when} \,\, q=0 \\ \end{array} \right. }

Isotropic Form Factor Intensity

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P_{sphere}(q) = \left\{ \begin{array}{c l} 36 \pi \Delta\rho^2 V_{sphere}^2 \frac{ (\sin(qR)-qR \cos(qR))^2 }{ (qR)^6 } & \mathrm{when} \,\, q\neq0\\ 4\pi \Delta\rho^2 V_{sphere}^2 & \mathrm{when} \,\, q=0\\ \end{array} \right. }

Sources

NCNR

From NCNR SANS Models documentation:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(q)=\frac{ \rm{scale} }{ V }\left[ \frac{ 3V(\Delta\rho)( \sin(qr)-qr \cos(qr)) }{ (qr)^3 } \right]^2 + \rm{background}}

• Parameters:
  1. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rm{scale}}  : Intensity scaling
  2. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r}  : sphere radius (Å)
  3. $\Delta \rho$ : scattering contrast (Å⁻²), $\Delta \rho =SLD_{core}-SLD_{solvent}$
  4. ${\rm {background}}$ : incoherent background (cm⁻¹)

Pedersen

From Pedersen review, Analysis of small-angle scattering data from colloids and polymer solutions: modeling and least-squares fitting Jan Skov Pedersen, Advances in Colloid and Interface Science 1997, 70, 171. doi: 10.1016/S0001-8686(97)00312-6

$F(q,r)={\frac {3\left[\sin(qr)-qr\cos(qr)\right]}{(qr)^{3}}}$

• Parameters:
  1. $r$ : sphere radius (Å)

IsGISAXS

From IsGISAXS, Born form factors:

$F(\mathbf {q} ,r)=4\pi r^{3}{\frac {\sin(qr)-qr\cos(qr)}{(qr)^{3}}}\exp {(iq_{z}r)}$

$V={\frac {4}{3}}\pi r^{3},S=\pi r^{2}$

• Parameters:
  1. $r$ : sphere radius (Å)

Code

    def sphere(self, q, r, scale=1.0, contrast=0.1, background=0.0):
        
        V = (4/3)*numpy.pi*(r**3)

        return (scale/V)*(( 3*V*contrast*(sin(q*r)-q*r*cos(q*r) )/( (q*r)**3 ) )**2) + background
        

Derivations

Form Factor

For a sphere of radius R, the volume is:

$V_{sphere}={\frac {4}{3}}\pi R^{3}$

We can use a spherical coordinates, where $\theta$ denotes the angle with respect to the $+q_{z}$ axis, and $\phi$ is the in-plane angle (i.e. with respect to the $+x$ axis):

${\begin{alignedat}{2}&\mathbf {r} =(x,y,z)=(r\sin \theta \cos \phi ,r\sin \theta \sin \phi ,r\cos \theta )\\&\mathbf {q} =(q_{x},q_{y},q_{z})\\&q=|\mathbf {q} |^{2}={\sqrt {q_{x}^{2}+q_{y}^{2}+q_{z}^{2}}}\end{alignedat}}$

Where the form factor is:

${\begin{alignedat}{2}F_{sphere}(\mathbf {q} )&=\int \limits _{V}e^{i\mathbf {q} \cdot \mathbf {r} }\mathrm {d} \mathbf {r} \\&=\int _{\phi =0}^{2\pi }\int _{\theta =0}^{\pi }\int _{r=0}^{R}e^{i\mathbf {q} \cdot \mathbf {r} }r^{2}\mathrm {d} r\sin \theta \mathrm {d} \theta \mathrm {d} \phi \\\end{alignedat}}$

We take advantage of spherical symmetry. E.g. we can rotate any q onto a particular axis, such as $q_{z}$. So that:

$\mathbf {q} =(0,0,q_{z})$

${\begin{alignedat}{2}\mathbf {q} \cdot \mathbf {r} &=q_{x}x+q_{y}y+q_{z}z\\&=q_{z}z\\&=qr\cos \theta \end{alignedat}}$

And so:

${\begin{alignedat}{2}F_{sphere}(q)&=\int _{0}^{2\pi }\mathrm {d} \phi \int _{0}^{\pi }\int _{0}^{R}e^{iqr\cos \theta }r^{2}\mathrm {d} r\sin \theta \mathrm {d} \theta \\&=[2\pi ]\int _{0}^{\pi }\int _{0}^{R}(\cos(qr\cos \theta )+i\sin(qr\cos \theta ))r^{2}\mathrm {d} r\sin \theta \mathrm {d} \theta \end{alignedat}}$

A simple variable substitution:

$u=qr\cos \theta$

$\mathrm {d} u=-qr\sin \theta \mathrm {d} \theta$

Yields:

${\begin{alignedat}{2}F_{sphere}(q)&=2\pi \int _{0}^{R}r^{2}\left[\int _{0}^{\pi }(\cos(u)+i\sin(u)){\frac {-\mathrm {d} u}{qr}}\right]\mathrm {d} r\\&=2\pi \int _{0}^{R}r^{2}{\frac {-1}{qr}}\left[\sin(u)-i\cos(u)\right]_{\theta =0}^{\pi }\mathrm {d} r\\&=2\pi \int _{0}^{R}{\frac {-r}{q}}\left[\sin(qr\cos \theta )-i\cos(qr\cos \theta )\right]_{\theta =0}^{\pi }\mathrm {d} r\\&=2\pi \int _{0}^{R}{\frac {-r}{q}}\left[\sin(-qr)-i\cos(-qr)-\sin(qr)+i\cos(qr)\right]\mathrm {d} r\\&=2\pi \int _{0}^{R}{\frac {r}{q}}\left[2\sin(qr)\right]\mathrm {d} r\\&={\frac {4\pi }{q}}\int _{0}^{R}r\sin(qr)\mathrm {d} r\\\end{alignedat}}$

Using the fact that:

$\int x\sin ax\;dx={\frac {\sin ax}{a^{2}}}-{\frac {x\cos ax}{a}}+C\,\!$

We integrate:

${\begin{alignedat}{2}F_{sphere}(q)&={\frac {4\pi }{q}}\left[{\frac {\sin(qr)}{q^{2}}}-{\frac {r\cos(qr)}{q}}\right]_{r=0}^{R}\\&={\frac {4\pi }{q}}\left[{\frac {\sin(qR)}{q^{2}}}-{\frac {R\cos(qR)}{q}}-{\frac {\sin(0)}{q^{2}}}+{\frac {0\cos(q0)}{q}}\right]\\&={\frac {4\pi }{1}}\left[{\frac {\sin(qR)}{q^{3}}}-{\frac {R\cos(qR)}{q^{2}}}-0+0\right]\\&=4\pi \left[{\frac {\sin(qR)}{q^{3}}}-{\frac {R\cos(qR)}{q^{2}}}\right]\\&=4\pi R^{3}\left[{\frac {\sin(qR)}{q^{3}R^{3}}}-{\frac {qR\cos(qR)}{q^{3}R^{3}}}\right]\\&={\frac {3\times 4\pi R^{3}}{3}}\left[{\frac {\sin(qR)-qRcos(qR)}{q^{3}R^{3}}}\right]\\&=3V_{sphere}{\frac {\sin(qR)-qR\cos(qR)}{(qR)^{3}}}\end{alignedat}}$

Form Factor at q=0

At very small q:

${\begin{alignedat}{2}\lim _{q\to 0}F_{sphere}(q)&={\frac {3V_{sphere}}{R^{3}}}\lim _{q\to 0}{\frac {\sin(qR)-qR\cos(qR)}{q^{3}}}\\&=4\pi \lim _{q\to 0}{\frac {\sin(qR)-qR\cos(qR)}{q^{3}}}\\&=4\pi \lim _{q\to 0}{\frac {1}{q^{3}}}\left[qR-{\frac {(qR)^{3}}{3!}}+...\right]-{\frac {R}{q^{2}}}\left[1-{\frac {(qR)^{2}}{2!}}+...\right]\\&=4\pi \lim _{q\to 0}{\frac {R}{q^{2}}}-{\frac {R^{3}}{3!}}+{\frac {O((qR)^{5})}{q^{3}}}-{\frac {R}{q^{2}}}+{\frac {R^{3}}{2!}}+{\frac {R\times O((qR)^{4})}{q^{2}}}\\&=4\pi \lim _{q\to 0}R^{3}\left({\frac {1}{2}}-{\frac {1}{6}}\right)+O(q^{2})\\&=4\pi \lim _{q\to 0}{\frac {R^{3}}{3}}+O(q^{2})\\&={\frac {4\pi R^{3}}{3}}\\&=V_{sphere}\\\end{alignedat}}$

Isotropic Form Factor Intensity

To average over all possible orientations, we use:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{alignat}{2} P(q) & = \int\limits_{S} | F(\mathbf{q}) |^2 \mathrm{d}\mathbf{s} \\ & = \int_{\phi=0}^{2\pi}\int_{\theta=0}^{\pi} | F(-q\sin\theta\cos\phi,q\sin\theta\sin\phi,q\cos\theta)|^2 \sin\theta\mathrm{d}\theta\mathrm{d}\phi \end{alignat} }

For a sphere:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{alignat}{2} P_{sphere}(q) & = \int_{0}^{2\pi}\int_{0}^{\pi} | F_{sphere}(q) |^2 \sin\theta\mathrm{d}\theta\mathrm{d}\phi \\ & = \int_{0}^{2\pi}\int_{0}^{\pi} \left| 3 V_{sphere} \frac{ \sin(qR)-qR \cos(qR) }{ (qR)^3 } \right|^2 \sin\theta\mathrm{d}\theta\mathrm{d}\phi \end{alignat} }

Note that the spherical symmetry guarantees that the integrand does not depend on $\phi$ or $\theta$:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{alignat}{2} P_{sphere}(q) & = \left( 3 V_{sphere} \frac{ \sin(qR)-qR \cos(qR) }{ (qR)^3 } \right)^2 \int_{0}^{2\pi}\int_{0}^{\pi} \sin\theta\mathrm{d}\theta\mathrm{d}\phi \\ & = 3^2 V_{sphere}^2 \left( \frac{ \sin(qR)-qR \cos(qR) }{ (qR)^3 } \right)^2 \left[\int_{0}^{2\pi}\mathrm{d}\phi\right]\left[\int_{0}^{\pi} \sin\theta\mathrm{d}\theta\right] \\ & = 9 V_{sphere}^2 \frac{ (\sin(qR)-qR \cos(qR))^2 }{ (qR)^6 } \left[ 2\pi \right]\left[ 2 \right] \\ & = 36 \pi V_{sphere}^2 \frac{ (\sin(qR)-qR \cos(qR))^2 }{ (qR)^6 } \\ \end{alignat} }

Isotropic Form Factor Intensity at q=0

At q=0, we expect:

$P_{sphere}\left(0\right)=4\pi V_{sphere}^{2}$

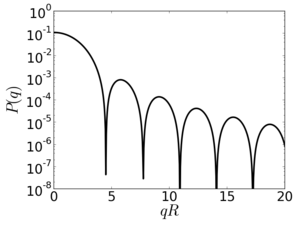
Isotropic Form Factor Intensity at large q

Note that:

${\begin{alignedat}{2}P_{sphere}(q)&=36\pi V_{sphere}^{2}{\frac {(\sin(qR)-qR\cos(qR))^{2}}{(qR)^{6}}}\\&=36\pi \left({\frac {4\pi R^{3}}{3}}\right)^{2}{\frac {(\sin(qR)-qR\cos(qR))^{2}}{q^{6}R^{6}}}\\&=64\pi ^{3}{\frac {(\sin(qR)-qR\cos(qR))^{2}}{q^{6}}}\\\end{alignedat}}$

For large q, the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -q R} term dominates the numerator:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{alignat}{2} \lim_{q \rightarrow \infty} P_{sphere}(q) & = \lim_{q \rightarrow \infty} 64 \pi^3 \frac{ (\sin(qR) - qR \cos(qR))^2 }{ q^6 } \\ & = \lim_{q \rightarrow \infty} 64 \pi^3 \frac{ q^2 R^2 \cos^2(qR) }{ q^6 } \\ & = 64 \pi^3 R^2 \lim_{q \rightarrow \infty} \frac{ \cos^2(qR) }{ q^4 } \\ \end{alignat} }

The oscillation of the numerator is overwhelmed by the decay of the denominator:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{alignat}{2} \lim_{q \rightarrow \infty} P_{sphere}(q) & \approx \frac{ 64 \pi^3 R^2 }{ q^4 } \\ \end{alignat} }