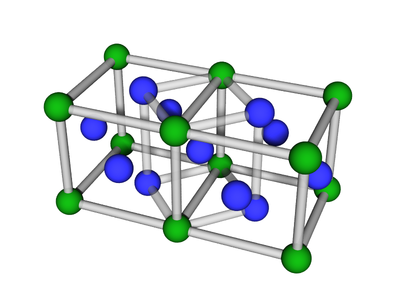
Lattice:FCC
FCC or face-centered cubic is a cubic lattice where the symmetry involves having additional atoms/particles sitting on the faces of the conceptual unit cell.
Contents
Canonical FCC
Symmetry
- Crystal Family: Cubic
- Crystal System: Cubic
- Bravais Lattice: F (fcc)
- Crystal class: Hexoctahedral
- Point Group: m3m
- Space Group: Fm3m
- Particles per unit cell:
- Volume of unit cell:
- Dimensionality:
- Projected d-dimensional volume:
- Solid angle:
- Nearest-neighbor distance:
- Assuming spherical particles of radius R:
- Particle volume fraction:
- Maximum volume fraction: when
Structure
One can also consider the FCC to be a distorted BCC:
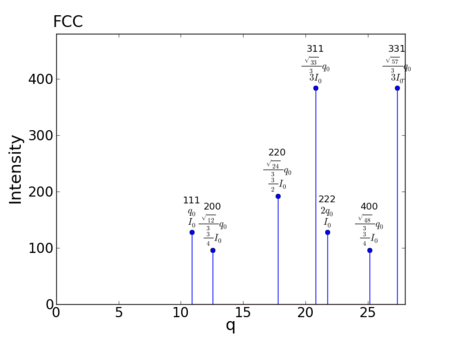
Reciprocal-Space Peaks
- Allowed reflections:
- Peak multiplicities:
- Peak positions:
- For a = 1.0:
peak q value h,k,l m f intensity 1: 10.882796185405 1,1,1 8 4 128 2: 12.566370614359 2,0,0 6 4 96 3: 17.771531752633 2,2,0 12 4 192 4: 20.838968152189 3,1,1 24 4 384 5: 21.765592370811 2,2,2 8 4 128 6: 25.132741228718 4,0,0 6 4 96 7: 27.387769797535 3,3,1 24 4 384 8: 28.099258924163 4,2,0 24 4 384 9: 30.781195923885 4,2,2 24 4 384 10: 32.648388556216 5,1,1 32 4 512 11: 35.543063505267 4,4,0 12 4 192 12: 37.171825569274 5,3,1 48 4 768 13: 37.699111843078 6,0,0 30 4 480 14: 39.738353063184 6,2,0 24 4 384 15: 41.201601388628 5,3,3 24 4 384 16: 41.677936304377 6,2,2 24 4 384 17: 43.531184741621 4,4,4 8 4 128 18: 44.870918174495 5,5,1 24 4 384 19: 45.308693596556 6,4,0 24 4 384 20: 47.019053434156 6,4,2 48 4 768 21: 48.262062105313 5,5,3 24 4 384 22: 51.812473373661 6,4,4 24 4 384 23: 53.314595257900 6,6,0 12 4 192 24: 54.413980927027 5,5,5 8 4 128 25: 54.775539595071 6,6,2 24 4 384 26: 58.941502773372 6,6,4 24 4 384 27: 65.296777112432 6,6,6 8 4 128
Face-centered Four-particle
A lattice where the unit cell has four distinct atoms/particles, arranged in an FCC-like way. The lattice has simple cubic symmetry.
Symmetry
- Crystal Family: Cubic
- Crystal System: Cubic
- Bravais Lattice: P (bcc)
- Crystal class: Hexoctahedral
- Point Group: m3m
- Space Group: Pm3m
- Particles per unit cell: (distinct)
- Volume of unit cell:
- Dimensionality:
- Projected d-dimensional volume:
- Solid angle:
- Nearest-neighbor distance:
Examples
Atomics
- NaCl (two distinct atoms) (a = 5.64 Å)