The following quantum mechanical argument is adapted from Boualem Hammouda's (NCNR) SANS tutorial.
Neutron energy
Consider first the energies of neutrons used in scattering experiments (recall the neutron mass is 1.67×10−27 kg). A thermal neutron (~100°C) would have energy of:

The velocity of such neutrons is ~3000 m/s, and the momentum is  . Finally, the deBroglie wavelength would be:
. Finally, the deBroglie wavelength would be:

A cold neutron (~18 K) would have energy of 4×10−22 J = 2 meV, velocity of ~660 m/s, and wavelength of 6 Å.
Potential well
Consider a neutron of energy  interacting with a nucleus, which exhibits an attractive square well of depth
interacting with a nucleus, which exhibits an attractive square well of depth  and width
and width  ; where
; where  (the depth of the well is ~MeV). The Schrödinger equation is:
(the depth of the well is ~MeV). The Schrödinger equation is:
![{\displaystyle \left[-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}+V(r)\right]\psi (r)=E\psi (r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1686f50dbe58c065a013a0ff19c35a4975229a2)
Outside of the square-well ( ),
),  , and so the equation is solved as simply:
, and so the equation is solved as simply:

where  . Inside the square-well (
. Inside the square-well ( ), the potential is
), the potential is  , and the solution becomes:
, and the solution becomes:

where  . The two solutions are subject to a continuity boundary condition at
. The two solutions are subject to a continuity boundary condition at  :
:

Note that  ; because of the small neutron mass and energy (see above), as well as the small size of a nucleus (femtometers). Therefore:
; because of the small neutron mass and energy (see above), as well as the small size of a nucleus (femtometers). Therefore:

and so:

And from equating the derivatives:

Combining the two results yields:

This final equation gives a first-order estimate for the scattering length, b, given the radius of the nucleus (R ~ 10−15 m) and the depth of the potential well (V0 ~ MeV).
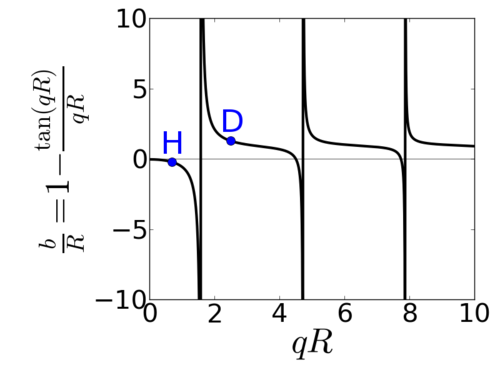
The extreme variation of b/R as a function of qR means that with each nucleon added, the scattering length jumps to a very different value. This also demonstrates why the scattering length can be negative (indicative of negative phase shift). This model should only be taken qualitatively, of course (e.g. we have neglected absorption, as well as the detailed form of the nuclear potential).







![{\displaystyle \left[-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}+V(r)\right]\psi (r)=E\psi (r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1686f50dbe58c065a013a0ff19c35a4975229a2)















