Wave packet
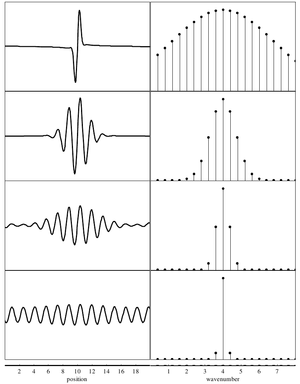
A wave packet is a localized wavelike perturbation, which appears frequently in quantum descriptions of particles. For instance, incident x-rays during scattering experiments can be thought of as wave-packets.
Contents
Position-momentum tradeoff
The wave-packet can be described as a wavefunction in either position-space or momentum-space:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi(x) = \frac{1}{\sqrt{2 \pi}} \int \tilde{\psi}(k) e^{i k x } \mathrm{d}k }
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{\psi}(k) = \frac{1}{\sqrt{2 \pi}} \int {\psi}(x) e^{-i k x } \mathrm{d}x }
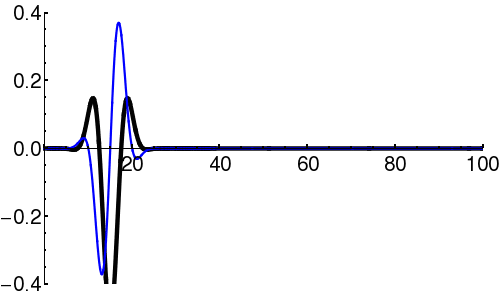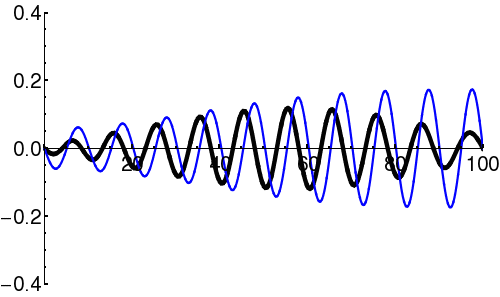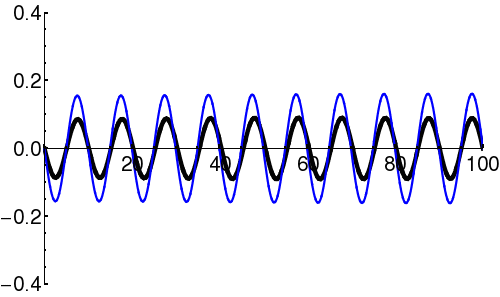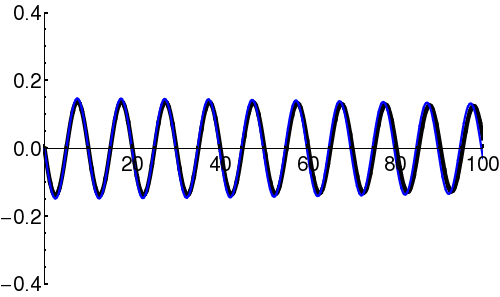
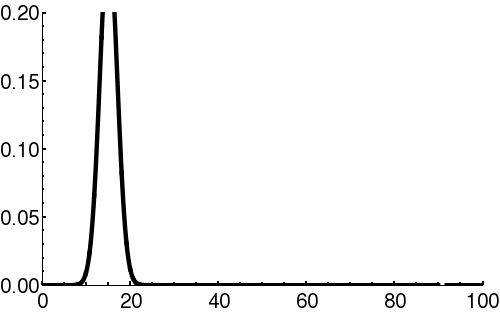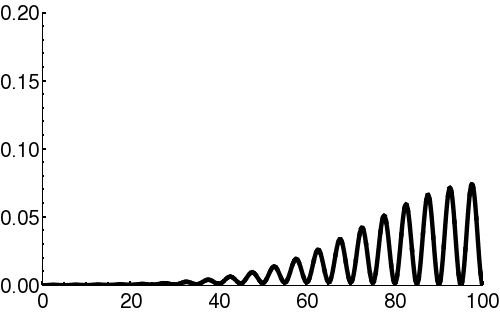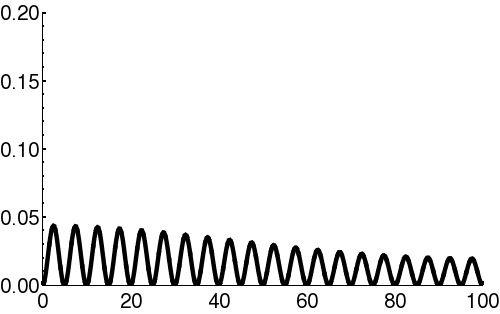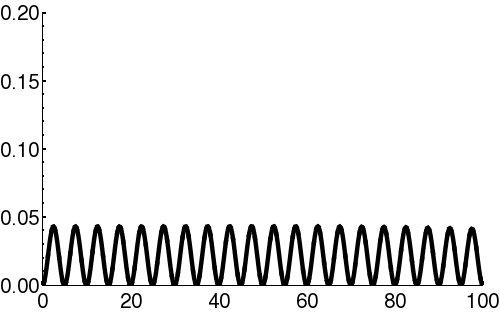
Note that these two descriptions are Fourier transforms of one another. Thus, there is an inherent tradeoff between the 'spread' of a wave-packet in position-space vs. momentum-space.
Wave-particle duality
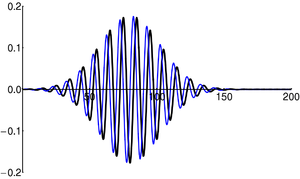
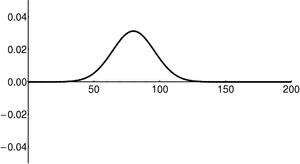
In the context of quantum mechanics, particles can be thought of as wave-packets. That is, quantum particles are neither ideal point-like particles, nor ideal plane-waves. They are instead intermediate objects, which are certainly wave-like (e.g. can undergo interference), but also somewhat localized. The classical concepts of 'particle' (perfectly localized; mathematically a delta-function), and 'wave' (oscillation with a single well-defined wavelength, spread infinitely over all space) can be viewed as limited cases of the general wave-packet. These limiting cases are only conceptual: in reality neither can exist.
Components
In quantum mechanics, the wave-packet necessarily has both real and imaginary components.
Propagation and Interaction
Wave-packets can propagate, frequently with dispersion (which induces spatial spread of the envelope). Wave-packets can interact with barriers (defined by, e.g., some potential function), and interfere with themselves.