|
|
| (One intermediate revision by the same user not shown) |
| Line 34: |
Line 34: |
| | \right. | | \right. |
| | </math> | | </math> |
| | + | |
| | + | [[Image:Sphere form factor.png|thumb|center|300px]] |
| | | | |
| | ==Sources== | | ==Sources== |
| Line 43: |
Line 45: |
| | *# <math>r</math> : sphere radius (Å) | | *# <math>r</math> : sphere radius (Å) |
| | *# <math>\Delta\rho</math> : scattering contrast (Å<sup>−2</sup>), <math>\Delta\rho = SLD_{core} - SLD_{solvent}</math> | | *# <math>\Delta\rho</math> : scattering contrast (Å<sup>−2</sup>), <math>\Delta\rho = SLD_{core} - SLD_{solvent}</math> |
| − | *# <math>\rm{background}</math> : incoherent background (cm<sup>−1</sup>) | + | *# <math>\rm{background}</math> : incoherent [[background]] (cm<sup>−1</sup>) |
| | | | |
| | ====Pedersen==== | | ====Pedersen==== |
Latest revision as of 11:57, 14 November 2014
This page provides the equations for calculating the form factor of a sphere (including derivations).
Equations
For spheres of radius R (volume  ):
):
Form Factor Amplitude

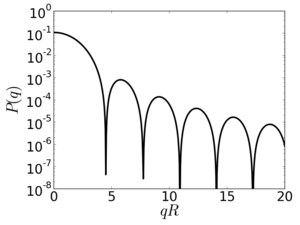
Isotropic Form Factor Intensity

Sources
NCNR
From NCNR SANS Models documentation:
![{\displaystyle P(q)={\frac {\rm {scale}}{V}}\left[{\frac {3V(\Delta \rho )(\sin(qr)-qr\cos(qr))}{(qr)^{3}}}\right]^{2}+{\rm {background}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6e1714184b5eff839f00ecf09f8baa011ded11d)
- Parameters:
 : Intensity scaling
: Intensity scaling : sphere radius (Å)
: sphere radius (Å) : scattering contrast (Å−2),
: scattering contrast (Å−2), 
 : incoherent background (cm−1)
: incoherent background (cm−1)
Pedersen
From Pedersen review, Analysis of small-angle scattering data from colloids and polymer solutions: modeling and least-squares fitting Jan Skov Pedersen, Advances in Colloid and Interface Science 1997, 70, 171. doi: 10.1016/S0001-8686(97)00312-6
![{\displaystyle F(q,r)={\frac {3\left[\sin(qr)-qr\cos(qr)\right]}{(qr)^{3}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07ef7f382375cf0850e95d5518c0a37acfdb0a6b)
- Parameters:
 : sphere radius (Å)
: sphere radius (Å)
IsGISAXS
From IsGISAXS, Born form factors:


- Parameters:
 : sphere radius (Å)
: sphere radius (Å)
Code
def sphere(self, q, r, scale=1.0, contrast=0.1, background=0.0):
V = (4/3)*numpy.pi*(r**3)
return (scale/V)*(( 3*V*contrast*(sin(q*r)-q*r*cos(q*r) )/( (q*r)**3 ) )**2) + background
Derivations
Form Factor
For a sphere of radius R, the volume is:

We can use a spherical coordinates, where  denotes the angle with respect to the
denotes the angle with respect to the  axis, and
axis, and  is the in-plane angle (i.e. with respect to the
is the in-plane angle (i.e. with respect to the  axis):
axis):

Where the form factor is:

We take advantage of spherical symmetry. E.g. we can rotate any q onto a particular axis, such as  . So that:
. So that:


And so:
![{\displaystyle {\begin{alignedat}{2}F_{sphere}(q)&=\int _{0}^{2\pi }\mathrm {d} \phi \int _{0}^{\pi }\int _{0}^{R}e^{iqr\cos \theta }r^{2}\mathrm {d} r\sin \theta \mathrm {d} \theta \\&=[2\pi ]\int _{0}^{\pi }\int _{0}^{R}(\cos(qr\cos \theta )+i\sin(qr\cos \theta ))r^{2}\mathrm {d} r\sin \theta \mathrm {d} \theta \end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79b3e396c15c16fd54b326f059e1fab7c932a6ac)
A simple variable substitution:


Yields:
![{\displaystyle {\begin{alignedat}{2}F_{sphere}(q)&=2\pi \int _{0}^{R}r^{2}\left[\int _{0}^{\pi }(\cos(u)+i\sin(u)){\frac {-\mathrm {d} u}{qr}}\right]\mathrm {d} r\\&=2\pi \int _{0}^{R}r^{2}{\frac {-1}{qr}}\left[\sin(u)-i\cos(u)\right]_{\theta =0}^{\pi }\mathrm {d} r\\&=2\pi \int _{0}^{R}{\frac {-r}{q}}\left[\sin(qr\cos \theta )-i\cos(qr\cos \theta )\right]_{\theta =0}^{\pi }\mathrm {d} r\\&=2\pi \int _{0}^{R}{\frac {-r}{q}}\left[\sin(-qr)-i\cos(-qr)-\sin(qr)+i\cos(qr)\right]\mathrm {d} r\\&=2\pi \int _{0}^{R}{\frac {r}{q}}\left[2\sin(qr)\right]\mathrm {d} r\\&={\frac {4\pi }{q}}\int _{0}^{R}r\sin(qr)\mathrm {d} r\\\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/023bb7e3e1e90fa1edae4b82c4b0337e47097b88)
Using the fact that:

We integrate:
![{\displaystyle {\begin{alignedat}{2}F_{sphere}(q)&={\frac {4\pi }{q}}\left[{\frac {\sin(qr)}{q^{2}}}-{\frac {r\cos(qr)}{q}}\right]_{r=0}^{R}\\&={\frac {4\pi }{q}}\left[{\frac {\sin(qR)}{q^{2}}}-{\frac {R\cos(qR)}{q}}-{\frac {\sin(0)}{q^{2}}}+{\frac {0\cos(q0)}{q}}\right]\\&={\frac {4\pi }{1}}\left[{\frac {\sin(qR)}{q^{3}}}-{\frac {R\cos(qR)}{q^{2}}}-0+0\right]\\&=4\pi \left[{\frac {\sin(qR)}{q^{3}}}-{\frac {R\cos(qR)}{q^{2}}}\right]\\&=4\pi R^{3}\left[{\frac {\sin(qR)}{q^{3}R^{3}}}-{\frac {qR\cos(qR)}{q^{3}R^{3}}}\right]\\&={\frac {3\times 4\pi R^{3}}{3}}\left[{\frac {\sin(qR)-qRcos(qR)}{q^{3}R^{3}}}\right]\\&=3V_{sphere}{\frac {\sin(qR)-qR\cos(qR)}{(qR)^{3}}}\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8835c5e095f484fc09fb52319f76de8de2c11b42)
Form Factor at q=0
At very small q:
![{\displaystyle {\begin{alignedat}{2}\lim _{q\to 0}F_{sphere}(q)&={\frac {3V_{sphere}}{R^{3}}}\lim _{q\to 0}{\frac {\sin(qR)-qR\cos(qR)}{q^{3}}}\\&=4\pi \lim _{q\to 0}{\frac {\sin(qR)-qR\cos(qR)}{q^{3}}}\\&=4\pi \lim _{q\to 0}{\frac {1}{q^{3}}}\left[qR-{\frac {(qR)^{3}}{3!}}+...\right]-{\frac {R}{q^{2}}}\left[1-{\frac {(qR)^{2}}{2!}}+...\right]\\&=4\pi \lim _{q\to 0}{\frac {R}{q^{2}}}-{\frac {R^{3}}{3!}}+{\frac {O((qR)^{5})}{q^{3}}}-{\frac {R}{q^{2}}}+{\frac {R^{3}}{2!}}+{\frac {R\times O((qR)^{4})}{q^{2}}}\\&=4\pi \lim _{q\to 0}R^{3}\left({\frac {1}{2}}-{\frac {1}{6}}\right)+O(q^{2})\\&=4\pi \lim _{q\to 0}{\frac {R^{3}}{3}}+O(q^{2})\\&={\frac {4\pi R^{3}}{3}}\\&=V_{sphere}\\\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/406b696bd44689e072933a91d96496f079c535a1)
Isotropic Form Factor Intensity
To average over all possible orientations, we use:

For a sphere:

Note that the spherical symmetry guarantees that the integrand does not depend on  or
or  :
:
![{\displaystyle {\begin{alignedat}{2}P_{sphere}(q)&=\left(3V_{sphere}{\frac {\sin(qR)-qR\cos(qR)}{(qR)^{3}}}\right)^{2}\int _{0}^{2\pi }\int _{0}^{\pi }\sin \theta \mathrm {d} \theta \mathrm {d} \phi \\&=3^{2}V_{sphere}^{2}\left({\frac {\sin(qR)-qR\cos(qR)}{(qR)^{3}}}\right)^{2}\left[\int _{0}^{2\pi }\mathrm {d} \phi \right]\left[\int _{0}^{\pi }\sin \theta \mathrm {d} \theta \right]\\&=9V_{sphere}^{2}{\frac {(\sin(qR)-qR\cos(qR))^{2}}{(qR)^{6}}}\left[2\pi \right]\left[2\right]\\&=36\pi V_{sphere}^{2}{\frac {(\sin(qR)-qR\cos(qR))^{2}}{(qR)^{6}}}\\\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7760e0148f5c1f2a899313a0ee6f52fa437dbb26)
Isotropic Form Factor Intensity at q=0
At q=0, we expect:

Isotropic Form Factor Intensity at large q
Note that:

For large q, the  term dominates the numerator:
term dominates the numerator:

The oscillation of the numerator is overwhelmed by the decay of the denominator:





![{\displaystyle P(q)={\frac {\rm {scale}}{V}}\left[{\frac {3V(\Delta \rho )(\sin(qr)-qr\cos(qr))}{(qr)^{3}}}\right]^{2}+{\rm {background}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6e1714184b5eff839f00ecf09f8baa011ded11d)





![{\displaystyle F(q,r)={\frac {3\left[\sin(qr)-qr\cos(qr)\right]}{(qr)^{3}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07ef7f382375cf0850e95d5518c0a37acfdb0a6b)












![{\displaystyle {\begin{alignedat}{2}F_{sphere}(q)&=\int _{0}^{2\pi }\mathrm {d} \phi \int _{0}^{\pi }\int _{0}^{R}e^{iqr\cos \theta }r^{2}\mathrm {d} r\sin \theta \mathrm {d} \theta \\&=[2\pi ]\int _{0}^{\pi }\int _{0}^{R}(\cos(qr\cos \theta )+i\sin(qr\cos \theta ))r^{2}\mathrm {d} r\sin \theta \mathrm {d} \theta \end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79b3e396c15c16fd54b326f059e1fab7c932a6ac)


![{\displaystyle {\begin{alignedat}{2}F_{sphere}(q)&=2\pi \int _{0}^{R}r^{2}\left[\int _{0}^{\pi }(\cos(u)+i\sin(u)){\frac {-\mathrm {d} u}{qr}}\right]\mathrm {d} r\\&=2\pi \int _{0}^{R}r^{2}{\frac {-1}{qr}}\left[\sin(u)-i\cos(u)\right]_{\theta =0}^{\pi }\mathrm {d} r\\&=2\pi \int _{0}^{R}{\frac {-r}{q}}\left[\sin(qr\cos \theta )-i\cos(qr\cos \theta )\right]_{\theta =0}^{\pi }\mathrm {d} r\\&=2\pi \int _{0}^{R}{\frac {-r}{q}}\left[\sin(-qr)-i\cos(-qr)-\sin(qr)+i\cos(qr)\right]\mathrm {d} r\\&=2\pi \int _{0}^{R}{\frac {r}{q}}\left[2\sin(qr)\right]\mathrm {d} r\\&={\frac {4\pi }{q}}\int _{0}^{R}r\sin(qr)\mathrm {d} r\\\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/023bb7e3e1e90fa1edae4b82c4b0337e47097b88)

![{\displaystyle {\begin{alignedat}{2}F_{sphere}(q)&={\frac {4\pi }{q}}\left[{\frac {\sin(qr)}{q^{2}}}-{\frac {r\cos(qr)}{q}}\right]_{r=0}^{R}\\&={\frac {4\pi }{q}}\left[{\frac {\sin(qR)}{q^{2}}}-{\frac {R\cos(qR)}{q}}-{\frac {\sin(0)}{q^{2}}}+{\frac {0\cos(q0)}{q}}\right]\\&={\frac {4\pi }{1}}\left[{\frac {\sin(qR)}{q^{3}}}-{\frac {R\cos(qR)}{q^{2}}}-0+0\right]\\&=4\pi \left[{\frac {\sin(qR)}{q^{3}}}-{\frac {R\cos(qR)}{q^{2}}}\right]\\&=4\pi R^{3}\left[{\frac {\sin(qR)}{q^{3}R^{3}}}-{\frac {qR\cos(qR)}{q^{3}R^{3}}}\right]\\&={\frac {3\times 4\pi R^{3}}{3}}\left[{\frac {\sin(qR)-qRcos(qR)}{q^{3}R^{3}}}\right]\\&=3V_{sphere}{\frac {\sin(qR)-qR\cos(qR)}{(qR)^{3}}}\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8835c5e095f484fc09fb52319f76de8de2c11b42)
![{\displaystyle {\begin{alignedat}{2}\lim _{q\to 0}F_{sphere}(q)&={\frac {3V_{sphere}}{R^{3}}}\lim _{q\to 0}{\frac {\sin(qR)-qR\cos(qR)}{q^{3}}}\\&=4\pi \lim _{q\to 0}{\frac {\sin(qR)-qR\cos(qR)}{q^{3}}}\\&=4\pi \lim _{q\to 0}{\frac {1}{q^{3}}}\left[qR-{\frac {(qR)^{3}}{3!}}+...\right]-{\frac {R}{q^{2}}}\left[1-{\frac {(qR)^{2}}{2!}}+...\right]\\&=4\pi \lim _{q\to 0}{\frac {R}{q^{2}}}-{\frac {R^{3}}{3!}}+{\frac {O((qR)^{5})}{q^{3}}}-{\frac {R}{q^{2}}}+{\frac {R^{3}}{2!}}+{\frac {R\times O((qR)^{4})}{q^{2}}}\\&=4\pi \lim _{q\to 0}R^{3}\left({\frac {1}{2}}-{\frac {1}{6}}\right)+O(q^{2})\\&=4\pi \lim _{q\to 0}{\frac {R^{3}}{3}}+O(q^{2})\\&={\frac {4\pi R^{3}}{3}}\\&=V_{sphere}\\\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/406b696bd44689e072933a91d96496f079c535a1)


![{\displaystyle {\begin{alignedat}{2}P_{sphere}(q)&=\left(3V_{sphere}{\frac {\sin(qR)-qR\cos(qR)}{(qR)^{3}}}\right)^{2}\int _{0}^{2\pi }\int _{0}^{\pi }\sin \theta \mathrm {d} \theta \mathrm {d} \phi \\&=3^{2}V_{sphere}^{2}\left({\frac {\sin(qR)-qR\cos(qR)}{(qR)^{3}}}\right)^{2}\left[\int _{0}^{2\pi }\mathrm {d} \phi \right]\left[\int _{0}^{\pi }\sin \theta \mathrm {d} \theta \right]\\&=9V_{sphere}^{2}{\frac {(\sin(qR)-qR\cos(qR))^{2}}{(qR)^{6}}}\left[2\pi \right]\left[2\right]\\&=36\pi V_{sphere}^{2}{\frac {(\sin(qR)-qR\cos(qR))^{2}}{(qR)^{6}}}\\\end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7760e0148f5c1f2a899313a0ee6f52fa437dbb26)




