Difference between revisions of "Quantum Mechanics"
KevinYager (talk | contribs) (→Wave packet) |
KevinYager (talk | contribs) (→Density Matrices) |
||
| (27 intermediate revisions by the same user not shown) | |||
| Line 71: | Line 71: | ||
| orthogonal | | orthogonal | ||
|} | |} | ||
| − | An operator defines a | + | An operator defines a particularly convenient basis: one can always expand <math>\psi</math> using the basis defined by an operator, in which case the <math>\psi_n</math> above are the eigenvectors (or eigenstates) of that basis. This can also be viewed as a vector in the Hilbert space. The Dirac notation (bra-ket notation) is useful in this regard. A particular state is a (column) vector: |
:<math> | :<math> | ||
| \psi \rangle = \begin{bmatrix} c_1 \\ c_2 \\ \vdots \\ c_n \end{bmatrix} | | \psi \rangle = \begin{bmatrix} c_1 \\ c_2 \\ \vdots \\ c_n \end{bmatrix} | ||
| Line 103: | Line 103: | ||
\psi(x) = \alpha \psi_1(x) + \beta \psi_2(x) | \psi(x) = \alpha \psi_1(x) + \beta \psi_2(x) | ||
</math> | </math> | ||
| − | This leads to a notable consequence: | + | where <math>\scriptstyle \alpha</math> and <math>\scriptstyle \beta</math> are complex-valued coefficients. This leads to a notable consequence: |
:<math> | :<math> | ||
\begin{alignat}{2} | \begin{alignat}{2} | ||
| Line 118: | Line 118: | ||
! Integral Notation | ! Integral Notation | ||
! Dirac Notation | ! Dirac Notation | ||
| + | ! Matrix Notation | ||
|- | |- | ||
| − | | <math>\ | + | | <math> \psi = \sum_n c_n \psi_n </math> |
| − | | <math> \ | + | | <math> |
| + | \begin{alignat}{2} | ||
| + | |\psi\rangle & = c_1 | \psi_1 \rangle + c_2 | \psi_2 \rangle + c_3 | \psi_3 \rangle + \cdots \\ | ||
| + | & = \sum_n c_n | \psi_n \rangle | ||
| + | \end{alignat} | ||
| + | </math> | ||
| + | | <math> |\psi\rangle = \begin{bmatrix} c_1 \\ c_2 \\ \vdots \\ c_n \end{bmatrix}</math> | ||
| + | |} | ||
| + | |||
| + | ==Operators== | ||
| + | Observables in QM appears as operators (<math>\hat{ O }</math>). | ||
| + | |||
| + | Examples: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Operator | ||
| + | ! Position basis | ||
| + | ! Momentum basis | ||
| + | |- | ||
| + | | Position | ||
| + | | align="center" | <math>\hat{x} = x</math> | ||
| + | | align="center" | <math> \hat{x} = i \hbar \frac{\partial}{\partial p}</math> | ||
| + | |- | ||
| + | | Momentum | ||
| + | | align="center" | <math>\hat{p} = - i \hbar \frac{\partial}{\partial x}</math> | ||
| + | | align="center" | <math> \hat{p} = p </math> | ||
| + | |- | ||
| + | | Hamiltonian | ||
| + | | colspan="2" align="center" | <math>\hat{H} = -\frac{\hbar^2}{2m}\nabla^2+ V(\mathbf{r},t)</math> | ||
| + | |- | ||
| + | | Energy | ||
| + | | colspan="2" align="center" | <math>\hat{E} = i\hbar\frac{\partial}{\partial t}</math> | ||
| + | |||
|} | |} | ||
| − | The | + | ==Commutators== |
| + | The commutator is a useful function for evaluating quantum objects. It is defined by: | ||
| + | :<math> \left [ \hat{A}, \hat{B} \right ] = \hat{A} \hat{B} - \hat{B} \hat{A} </math> | ||
| + | The commutator can be thought of as a composite operator, which can thus act on a wavefunction: | ||
| + | :<math> \left [ \hat{A}, \hat{B} \right ] \psi = \hat{A} \hat{B} \psi - \hat{B} \hat{A} \psi</math> | ||
| + | The uncertainty relations are intimately tied to commutators of operators. For instance, for two non-commuting operators: | ||
| + | :<math> | ||
| + | [ \hat{A}, \, \hat{B} ] = c \mathbf{1} | ||
| + | </math> | ||
| + | Then the related uncertainties follow: | ||
| + | :<math> | ||
| + | \Delta_{\psi}A \Delta_{\psi}B \geq \frac{1}{2} |\langle \psi | [ \hat{A}, \, \hat{B} ] | \psi \rangle| | ||
| + | </math> | ||
| + | Therefore, non-commuting operators have a indeterminacy relation between their associated observables; and the commutation relation provides the bound on this inter-relation. The two observables cannot both be simultaneously definite (the wavefunction cannot be in a state that is simultaneously an eigenstate of both operators, so it cannot have a definite eigenvalue for both of the observables). On the other hand, if two operators commute: | ||
| + | :<math> | ||
| + | [ \hat{A}, \, \hat{B} ] = \mathbf{0} | ||
| + | </math> | ||
| + | Then the wavefunction can be in a state that is simultaneously an eigenstate of both operators. There is thus no restriction on both observables (''A'' and ''B'') being simultaneously definite (known to arbitrary precision). | ||
| + | :<math> | ||
| + | \Delta_{\psi}A \Delta_{\psi}B \geq 0 | ||
| + | </math> | ||
| + | |||
| + | ==Measurement== | ||
| + | For state <math>\psi</math> and linear map <math>\langle \phi |</math>: | ||
| + | |||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
! Integral Notation | ! Integral Notation | ||
! Dirac Notation | ! Dirac Notation | ||
| + | ! Matrix Notation | ||
|- | |- | ||
| − | | <math> \psi | + | | <math> \psi \in V </math> <br/> <math> \psi = \sum_n c_n \psi_n </math> |
| − | | <math> |\psi\rangle = c_1 | | + | | <math> |
| + | \begin{alignat}{2} | ||
| + | |\psi\rangle & = c_1 | \psi_1 \rangle + c_2 | \psi_2 \rangle + c_3 | \psi_3 \rangle + \cdots \\ | ||
| + | & = \sum_n c_n | \psi_n \rangle | ||
| + | \end{alignat} | ||
| + | </math> | ||
| + | | <math> |\psi\rangle = \begin{bmatrix} c_1 \\ c_2 \\ \vdots \\ c_n \end{bmatrix}</math> | ||
| + | |- | ||
| + | | <math> f_{\phi} \in V^* </math> | ||
| + | | <math> \langle \phi | = a_1^* \langle \phi_1 | + a_2^* \langle \phi_2 | + a_3^* \langle \phi_3 | + \dots </math> | ||
| + | | <math> \langle \phi | = \begin{bmatrix} a_1^* & a_2^* & \dots & a_n^* \end{bmatrix} </math> | ||
| + | |||
|} | |} | ||
| + | The linear map <math>\langle \phi |</math> is a function (in the complex vector space <math>V^*</math>, dual to <math>V</math>) that maps from vector space <math>V</math> to <math>\mathbb{C}</math>. In conventional notation this operation would be performed using a function <math>f_{\phi}</math> applied to <math>\psi</math>: | ||
| − | + | :<math>f_{\phi}(\psi) = a_1^* \psi_1 + a_2^* \psi_2 + \dots + a_n^* \psi_n</math> | |
| − | |||
| − | + | In a quantum measurement, the transition of the wavefunction <math>\psi</math> into state <math>\phi</math> can be thought of as: | |
| − | |||
| − | |||
| − | |||
{| class="wikitable" | {| class="wikitable" | ||
| <math> \int \phi^* \psi \mathrm{d}x </math> | | <math> \int \phi^* \psi \mathrm{d}x </math> | ||
| <math> \langle \phi | \psi \rangle = a_1^*c_1 + a_2^*c_2 + a_3^*c_3 + \cdots </math> | | <math> \langle \phi | \psi \rangle = a_1^*c_1 + a_2^*c_2 + a_3^*c_3 + \cdots </math> | ||
|} | |} | ||
| − | When acting on a wavefunction with operator <math>\hat{ O }</math> the probability that the wavefunction ends up in state <math>\phi_n</math> is given by: | + | Thus <math>\scriptstyle \langle \phi | \psi \rangle </math> is the probability amplitude for the initial state <math>\scriptstyle \psi</math> to 'collapse' into the state <math>\scriptstyle \phi</math>. Measurements take the form of operators in QM. When acting on a wavefunction with operator <math>\hat{ O }</math> the probability that the wavefunction ends up in state <math>\phi_n</math> is given by: |
{| class="wikitable" | {| class="wikitable" | ||
| − | | <math> \Pr( O_n ) = | c_n |^2 </math> | + | | <math> \begin{alignat}{2} \Pr( O_n ) & = \left| \int \phi_n^* \psi \mathrm{d}x \right|^2 \\ & = \left| \int \phi_n^* \sum_m c_m \phi_m \mathrm{d}x \right|^2 \\ & = \left| c_n \int \phi_n^* \phi_n \mathrm{d}x \right|^2 \\ & = | c_n |^2 \end{alignat}</math> |
| − | | <math> \Pr( O_n ) = | \lang n | \psi \rang |^2 = | c_n |^2 </math> | + | | <math> \begin{alignat}{2} \Pr( O_n ) & = | \lang n | \psi \rang |^2 \\ & = | c_n |^2 \end{alignat}</math> |
|} | |} | ||
The solutions take the form of an eigenvalue problem: | The solutions take the form of an eigenvalue problem: | ||
| Line 195: | Line 262: | ||
==Entanglement== | ==Entanglement== | ||
| − | + | When systems (or Hilbert spaces) A and B interact, they become entangled. Before the interaction, the two systems are simply a composite system: | |
| + | :<math>|\psi\rangle_A \otimes |\phi\rangle_B</math> | ||
| + | At this level, states are separable. However, the composite system more generally should be written as: | ||
| + | : <math>|\psi\rangle_{AB} = \sum_{i,j} c_{ij} |i\rangle_A \otimes |j\rangle_B</math> | ||
| + | If all the coefficients can be written as <math>\scriptstyle c_{ij}= c^A_ic^B_j,</math>, then there is no coupling between the two states. We call the system '''separable''', since it can be decomposed into the two sub-systems: | ||
| + | :<math>|\psi\rangle_A = \sum_{i} c^A_{i} |i\rangle_A</math> | ||
| + | :<math>|\phi\rangle_B = \sum_{j} c^B_{j} |j\rangle_B</math> | ||
| + | However, if <math>\scriptstyle c_{ij} \neq c^A_ic^B_j</math>, then the states are non-separable, or '''entangled'''. | ||
| + | |||
| + | The entanglement of an observer (or simply measurement apparatus) can also be considered. For observer <math>\scriptstyle |\psi\rangle</math> performing measurement <math>\scriptstyle U</math> on system <math>\scriptstyle \sum a_n |S_n\rangle</math>: | ||
| + | :<math> | ||
| + | U(|\psi\rangle \otimes |S_n\rangle) = |\psi_n\rangle \otimes |S_n\rangle | ||
| + | </math> | ||
| + | This leads to the evolution: | ||
| + | :<math> | ||
| + | |\psi\rangle \otimes \sum a_n |S_n\rangle \to \sum a_n |\psi_n\rangle \otimes |S_n\rangle | ||
| + | </math> | ||
| + | Where the right-hand-side describes an entanglement between the observer and the system being studied. | ||
| + | |||
| + | ==Density Matrices== | ||
| + | The outer product of a ket with a bra defines a 2D matrix; i.e. a linear operator. | ||
| + | :<math> |\phi \rangle \langle \psi | = | ||
| + | \begin{bmatrix} \phi_1 \\ \phi_2 \\ \vdots \\ \phi_N \end{bmatrix} | ||
| + | \begin{bmatrix} \psi_1^* & \psi_2^* & \cdots & \psi_N^* \end{bmatrix} | ||
| + | = \begin{bmatrix} | ||
| + | \phi_1 \psi_1^* & \phi_1 \psi_2^* & \cdots & \phi_1 \psi_N^* \\ | ||
| + | \phi_2 \psi_1^* & \phi_2 \psi_2^* & \cdots & \phi_2 \psi_N^* \\ | ||
| + | \vdots & \vdots & \ddots & \vdots \\ | ||
| + | \phi_N \psi_1^* & \phi_N \psi_2^* & \cdots & \phi_N \psi_N^* \end{bmatrix} | ||
| + | </math> | ||
| + | Density matrices can be a useful way to visualize the interactions between states of a system, and time-evolution. Thus we can define the density matrix as: | ||
| + | :<math> | ||
| + | \rho(t) \equiv | \psi(t) \rangle \langle \psi(t) | | ||
| + | </math> | ||
| + | The elements of the density matrix can be interpreted as a form of quantum probability distribution. For instance, a '''pure state''' is given by a density matrix that has only a single non-zero term, along the diagonal: | ||
| + | :<math> | ||
| + | | \psi \rangle \langle \psi | = | ||
| + | \begin{bmatrix} | ||
| + | 1 & 0 \\ | ||
| + | 0 & 0 | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | By comparison, a '''mixed state''' is one where more than one diagonal term is non-zero, but off-diagonal terms are zero: | ||
| + | :<math> | ||
| + | | \psi \rangle \langle \psi | = | ||
| + | \begin{bmatrix} | ||
| + | 0.5 & 0 \\ | ||
| + | 0 & 0.5 | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | The diagonal terms of the density matrix will be real numbers (and can be interpreted as probabilities). The above matrix describes a classical mixture of different states. In the Copenhagen interpretation, this would be described as a situation where the system will randomly collapse into one of the possible states. Under MWI, it would instead be said that the various states are now non-interacting, and thus will evolve independently. | ||
| + | |||
| + | The most general case is where the off-diagonal terms are non-zero. These terms represent the interference aspects. Thus this describes an '''entangled state''': | ||
| + | :<math> | ||
| + | | \psi \rangle \langle \psi | = | ||
| + | \begin{bmatrix} | ||
| + | 0.36 & -0.48 i \\ | ||
| + | +0.48 i & 0.64 | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | The off-diagonal terms indicate the strength and nature of the interference between the states. Thus, the diagonal elements (<math>n=m</math>) capture the probability of occupying a certain state as <math>\rho_{nm} = \overline{c_n c_n^*} = p_n \geq 0 </math>The time-dependence often appears in these off-diagonal (<math>n\neq m</math>) terms as <math>\rho_{nm}(t) = \overline{c_n(t)c_m^*(t)} = \overline{c_n c_m^*} e^{-i \omega_{nm} t} </math>. | ||
| + | |||
| + | During decoherence, these off-diagonal terms are driven towards zero. | ||
==Decoherence== | ==Decoherence== | ||
Latest revision as of 15:45, 16 June 2021
Quantum mechanics is a theory that describes the interactions of all particles and systems. It underlies all physical phenomena, including scattering.
Contents
Wavefunction
A quantum system is completely specified by its Wave Function:
| Integral Notation | Dirac Notation |
|---|---|
The wavefunction is typically normalized:
| Integral Notation | Dirac Notation |
|---|---|
The distribution of the particle described by is given by:
| Integral Notation | Dirac Notation |
|---|---|
In the Copenhagen Interpretation, is the probability of finding the particle at location . In Universal Wave Function interpretations (e.g. MWI), can be thought of as the spatial distribution of the particle. The wavefunction contains all the information one can know about a system. It can thus be thought of as 'being' the particle/system in question. However, the wavefunction can be described in an infinite number of different ways. That is, there is not a unique basis for describing the wavefunction. So, for instance, one can describe the wavefunction using position-space or momentum-space:
These representations can be inter-related (c.f. Fourier transform):
State
Note that the wavefunction describes the state of the system; there are various choices of basis one can use as an expansion.
A basis should be orthonormal:
| Integral Notation | Dirac Notation | |
|---|---|---|
| normalized | ||
| orthogonal |
An operator defines a particularly convenient basis: one can always expand using the basis defined by an operator, in which case the above are the eigenvectors (or eigenstates) of that basis. This can also be viewed as a vector in the Hilbert space. The Dirac notation (bra-ket notation) is useful in this regard. A particular state is a (column) vector:
Which is a 'ket'. We define a 'bra' (the 'final state') as a (row) vector:
And note that the 'bra' is the conjuagte transpose of the 'ket':
Wave packet
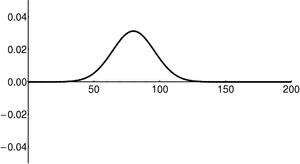
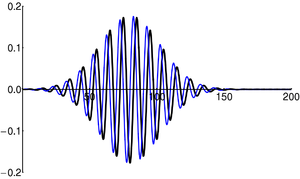
A wave packet is a localized wavelike perturbation. Particles in quantum mechanics can be thought of as wave-packets.
Note that "wave-particle duality" can be misleading. One can imagine a quantum particle as "both a wave and a particle"; however, it might be better to instead imagine it as a "wave packet". The 'particle' and 'wave' descriptions are really idealized limiting cases, which never appear in reality:
- A classical 'particle' is a point-like object. In QM would have a corresponding infinite spread in its momentum. Such an idealized (infinitely small) entity cannot truly exist.
- A classical 'wave' is a plane wave: an oscillation with a perfectly well-defined wavelength, extending infinitely in both directions. In QM, we indeed note that having a precisely-defined wavelength (momentum) implies infinite spatial spread (i.e. the wave fills the entire universe). Such a construct is not physically-realizable.
Heisenberg Indeterminacy Relations
(Also known as Heisenberg Uncertainty Principle.)
Superposition
If and are both allowed states for a given system, then the following state is also allowed:
where and are complex-valued coefficients. This leads to a notable consequence:
Notice that the final terms represent 'interference' between the two constituent states. This interference has no classical analogue; it is a quantum effect. Thus a superposition is not merely a 'joining' of the two states (e.g. "the particle can be in state 1 or state 2"), but a truly coherent interference between the two states. The superposition may be more generally written as:
| Integral Notation | Dirac Notation | Matrix Notation |
|---|---|---|
Operators
Observables in QM appears as operators ().
Examples:
| Operator | Position basis | Momentum basis |
|---|---|---|
| Position | ||
| Momentum | ||
| Hamiltonian | ||
| Energy | ||
Commutators
The commutator is a useful function for evaluating quantum objects. It is defined by:
The commutator can be thought of as a composite operator, which can thus act on a wavefunction:
The uncertainty relations are intimately tied to commutators of operators. For instance, for two non-commuting operators:
Then the related uncertainties follow:
Therefore, non-commuting operators have a indeterminacy relation between their associated observables; and the commutation relation provides the bound on this inter-relation. The two observables cannot both be simultaneously definite (the wavefunction cannot be in a state that is simultaneously an eigenstate of both operators, so it cannot have a definite eigenvalue for both of the observables). On the other hand, if two operators commute:
Then the wavefunction can be in a state that is simultaneously an eigenstate of both operators. There is thus no restriction on both observables (A and B) being simultaneously definite (known to arbitrary precision).
Measurement
For state and linear map :
| Integral Notation | Dirac Notation | Matrix Notation |
|---|---|---|
| |
||
The linear map is a function (in the complex vector space , dual to ) that maps from vector space to . In conventional notation this operation would be performed using a function applied to :
In a quantum measurement, the transition of the wavefunction into state can be thought of as:
Thus is the probability amplitude for the initial state to 'collapse' into the state . Measurements take the form of operators in QM. When acting on a wavefunction with operator the probability that the wavefunction ends up in state is given by:
The solutions take the form of an eigenvalue problem:
The allowed solutions of the equation, for operator , involve an eigenstate with associated eigenvalue . A measurement on a quantum system can be thought of as driving the wavefunction into an eigenstate defined by the operator; the value of the associated observable is then fixed to be the corresponding eigenvalue. (As noted above, the probability of ending up in a particular eigenstate is regulated by the coefficient of that eigenstate in the original wavefunction decomposition.)
Expectation value
A given operator, e.g. , implies an expectation value (for state ) of:
If the system is in an eigenstate of the operator:
We know that:
And so:
In other words, the expectation value of an eigenstate is simply the eigenvalue.
Schrödinger Equation
Time-independent equation
This simplified version of the Schrödinger equation can be used to solve for allowed stationary states. The general form is akin to the eigenvalue problems noted above: the energy operator () acts on the system state () to yield an energy eigenvalue ():
For a single non-relativistic particle, the Hamiltonian is known and the Schrödinger equation takes the form:
Time-dependent equation
More generally, the time-evolution of the wavefunction should be considered. The full version of the Schrödinger equation thus includes time dependence:
Again for a single non-relativistic particle, we can write more specifically that:
Entanglement
When systems (or Hilbert spaces) A and B interact, they become entangled. Before the interaction, the two systems are simply a composite system:
At this level, states are separable. However, the composite system more generally should be written as:
If all the coefficients can be written as , then there is no coupling between the two states. We call the system separable, since it can be decomposed into the two sub-systems:
However, if , then the states are non-separable, or entangled.
The entanglement of an observer (or simply measurement apparatus) can also be considered. For observer performing measurement on system :
This leads to the evolution:
Where the right-hand-side describes an entanglement between the observer and the system being studied.
Density Matrices
The outer product of a ket with a bra defines a 2D matrix; i.e. a linear operator.
Density matrices can be a useful way to visualize the interactions between states of a system, and time-evolution. Thus we can define the density matrix as:
The elements of the density matrix can be interpreted as a form of quantum probability distribution. For instance, a pure state is given by a density matrix that has only a single non-zero term, along the diagonal:
By comparison, a mixed state is one where more than one diagonal term is non-zero, but off-diagonal terms are zero:
The diagonal terms of the density matrix will be real numbers (and can be interpreted as probabilities). The above matrix describes a classical mixture of different states. In the Copenhagen interpretation, this would be described as a situation where the system will randomly collapse into one of the possible states. Under MWI, it would instead be said that the various states are now non-interacting, and thus will evolve independently.
The most general case is where the off-diagonal terms are non-zero. These terms represent the interference aspects. Thus this describes an entangled state:
The off-diagonal terms indicate the strength and nature of the interference between the states. Thus, the diagonal elements () capture the probability of occupying a certain state as The time-dependence often appears in these off-diagonal () terms as .
During decoherence, these off-diagonal terms are driven towards zero.
Decoherence
TBD






































![{\displaystyle \left[{\hat {A}},{\hat {B}}\right]={\hat {A}}{\hat {B}}-{\hat {B}}{\hat {A}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa7917e45fa532ccc9cfd210a2ac545e0b60b093)
![{\displaystyle \left[{\hat {A}},{\hat {B}}\right]\psi ={\hat {A}}{\hat {B}}\psi -{\hat {B}}{\hat {A}}\psi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/aba242fe64c7b4fff4f04c7cc9a06d9343cb8f4d)
![{\displaystyle [{\hat {A}},\,{\hat {B}}]=c\mathbf {1} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bb1292ad8435373fe98815260af1ca1fe691b11)
![{\displaystyle \Delta _{\psi }A\Delta _{\psi }B\geq {\frac {1}{2}}|\langle \psi |[{\hat {A}},\,{\hat {B}}]|\psi \rangle |}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cd60eeac6ece865cae0d7defd43fb741048ea7b)
![{\displaystyle [{\hat {A}},\,{\hat {B}}]=\mathbf {0} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fbdebb5225dff1e22c01bf00d38d4ef88d9ae76)
































![{\displaystyle E\Psi (\mathbf {r} )=\left[{\frac {-\hbar ^{2}}{2m}}\nabla ^{2}+V(\mathbf {r} )\right]\Psi (\mathbf {r} )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c51f6b87a0560f7ad79de32ad673a62fa4e32cab)

![{\displaystyle i\hbar {\frac {\partial }{\partial t}}\Psi (\mathbf {r} ,t)=\left[{\frac {-\hbar ^{2}}{2\mu }}\nabla ^{2}+V(\mathbf {r} ,t)\right]\Psi (\mathbf {r} ,t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2ae69999ed8b8551b217b9fbdcd8bf73490c82f)



















