Difference between revisions of "Wave packet"
KevinYager (talk | contribs) (→Position-momentum tradeoff) |
KevinYager (talk | contribs) (→Propagation and Interaction) |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 10: | Line 10: | ||
:<math> \tilde{\psi}(k) = \frac{1}{\sqrt{2 \pi}} \int {\psi}(x) e^{-i k x } \mathrm{d}x </math> | :<math> \tilde{\psi}(k) = \frac{1}{\sqrt{2 \pi}} \int {\psi}(x) e^{-i k x } \mathrm{d}x </math> | ||
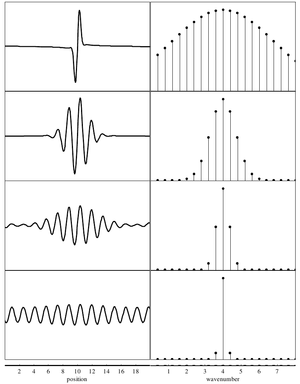
Note that these two descriptions are [[Fourier transform]]s of one another. Thus, there is an inherent tradeoff between the 'spread' of a wave-packet in position-space vs. momentum-space. | Note that these two descriptions are [[Fourier transform]]s of one another. Thus, there is an inherent tradeoff between the 'spread' of a wave-packet in position-space vs. momentum-space. | ||
| − | [[Image:Space tradeoff.png|center|thumb|Tradeoff between spread of a wave-packet in position-space (left) and momenum-space (right).]] | + | [[Image:Space tradeoff.png|center|thumb|300px|Tradeoff between spread of a wave-packet in position-space (left) and momenum-space (right).]] |
==Wave-particle duality== | ==Wave-particle duality== | ||
In the context of [[quantum mechanics]], particles can be thought of as wave-packets. That is, quantum particles are neither ideal point-like particles, nor ideal plane-waves. They are instead intermediate objects, which are certainly wave-like (e.g. can undergo interference), but also somewhat localized. The classical concepts of 'particle' (perfectly localized; mathematically a delta-function), and 'wave' (oscillation with a single well-defined wavelength, spread infinitely over all space) can be viewed as limited cases of the general wave-packet. These limiting cases are only conceptual: in reality neither can exist. | In the context of [[quantum mechanics]], particles can be thought of as wave-packets. That is, quantum particles are neither ideal point-like particles, nor ideal plane-waves. They are instead intermediate objects, which are certainly wave-like (e.g. can undergo interference), but also somewhat localized. The classical concepts of 'particle' (perfectly localized; mathematically a delta-function), and 'wave' (oscillation with a single well-defined wavelength, spread infinitely over all space) can be viewed as limited cases of the general wave-packet. These limiting cases are only conceptual: in reality neither can exist. | ||
| + | ==Components== | ||
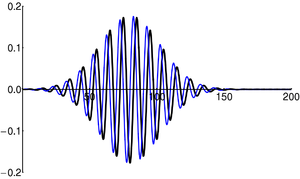
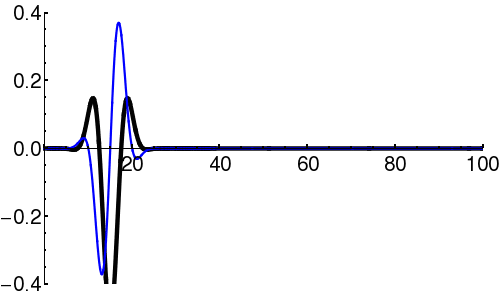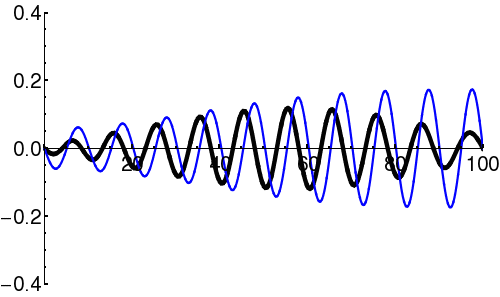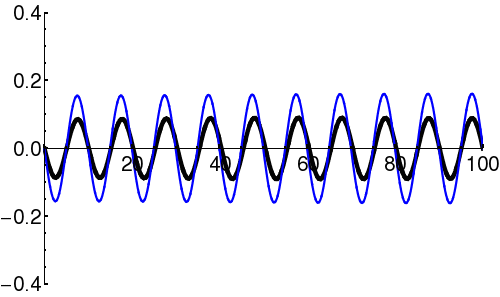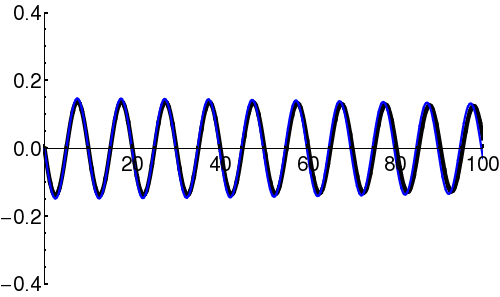
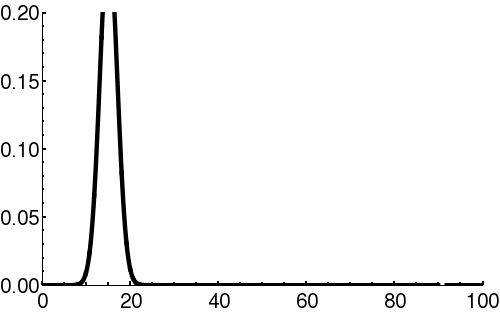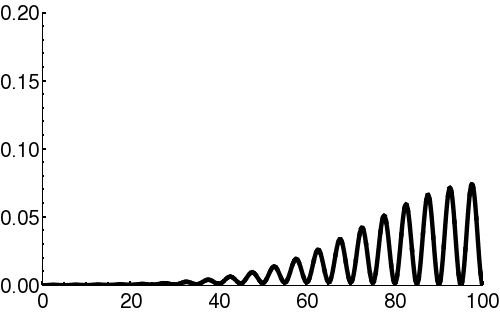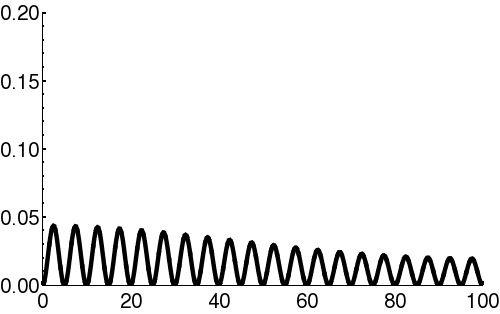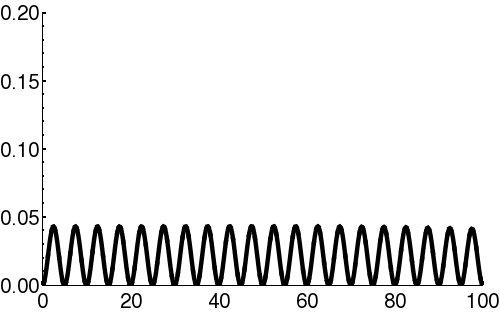
| + | In [[quantum mechanics]], the wave-packet necessarily has both real and imaginary components. | ||
| + | {| | ||
| + | | [[Image:Free packet1.png|300px|thumb|Components of the wavefunction (<math>\scriptstyle \psi(x) </math>) describing a propagating wave-packet. The black line is the real part, and the blue line is the imaginary part.]] | ||
| + | |- | ||
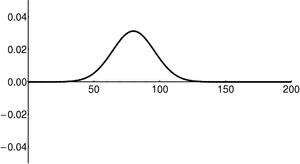
| + | | [[Image:Free packet2.png|300px|thumb|Square of the wavefunction (<math>\scriptstyle | \psi(x) |^2 </math>) for a propagating wave-packet. This describes the spatial spread of the function.]] | ||
| + | |} | ||
| + | |||
| + | ==Propagation and Interaction== | ||
| + | Wave-packets can propagate, frequently with dispersion (which induces spatial spread of the envelope). Wave-packets can interact with barriers (defined by, e.g., some potential function), and interfere with themselves. | ||
| + | |||
| + | {| | ||
| + | | [[Image:Wavepacket-Box-wavefunc3.gif|500px|thumb|Components of the wavefunction (<math>\scriptstyle \psi(x) </math>) describing a wave-packet bouncing inside a box-like potential. The black line is the real part, and the blue line is the imaginary part.]] | ||
| + | |- | ||
| + | | [[Image:Wavepacket-Box-sqr2.gif|500px|thumb|Square of the wavefunction (<math>\scriptstyle | \psi(x) |^2 </math>) for a wave-packet bouncing inside a box-like potential.]] | ||
| + | |} | ||
==See Also== | ==See Also== | ||
* [[Fourier transform]] | * [[Fourier transform]] | ||
* [http://en.wikipedia.org/wiki/Wave_packet Wikipedia: Wave packet] | * [http://en.wikipedia.org/wiki/Wave_packet Wikipedia: Wave packet] | ||
Latest revision as of 08:52, 3 November 2014
A wave packet is a localized wavelike perturbation, which appears frequently in quantum descriptions of particles. For instance, incident x-rays during scattering experiments can be thought of as wave-packets.
Contents
Position-momentum tradeoff
The wave-packet can be described as a wavefunction in either position-space or momentum-space:
Note that these two descriptions are Fourier transforms of one another. Thus, there is an inherent tradeoff between the 'spread' of a wave-packet in position-space vs. momentum-space.
Wave-particle duality
In the context of quantum mechanics, particles can be thought of as wave-packets. That is, quantum particles are neither ideal point-like particles, nor ideal plane-waves. They are instead intermediate objects, which are certainly wave-like (e.g. can undergo interference), but also somewhat localized. The classical concepts of 'particle' (perfectly localized; mathematically a delta-function), and 'wave' (oscillation with a single well-defined wavelength, spread infinitely over all space) can be viewed as limited cases of the general wave-packet. These limiting cases are only conceptual: in reality neither can exist.
Components
In quantum mechanics, the wave-packet necessarily has both real and imaginary components.
Propagation and Interaction
Wave-packets can propagate, frequently with dispersion (which induces spatial spread of the envelope). Wave-packets can interact with barriers (defined by, e.g., some potential function), and interfere with themselves.