Difference between revisions of "Scattering"
KevinYager (talk | contribs) |
KevinYager (talk | contribs) (→Theory) |
||
| Line 23: | Line 23: | ||
==Theory== | ==Theory== | ||
| − | The mathematical form of scattering is closely related to the [[Fourier transform]]. The sample's realspace density distribution is Fourier transformed into an abstract 3D [[reciprocal-space]]; scattering probes this inverse space. | + | The mathematical form of scattering is closely related to the [[Fourier transform]]. The sample's [[realspace]] density distribution is Fourier transformed into an abstract 3D [[reciprocal-space]]; scattering probes this inverse space. |
Revision as of 09:36, 14 October 2014
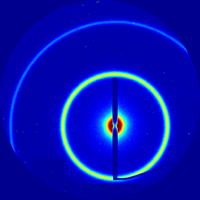
Scattering broadly refers to experimental techniques that use the interaction between radiation and matter to elucidate structure. In x-ray scattering, a collimated x-ray beam is directed at a sample of interest. The incident x-rays scatter off of all the atoms/particles in the sample. Because of the wavelike nature of x-rays (which are simply high-energy photons; i.e. electromagnetic rays), the scattered waves interfere with one another, leading to constructive interference at some angles, but destructive interference at other angles. The end result is a pattern of scattered radiation (as a function of angle with respect to the direct beam) that encodes the microscopic, nanoscopic, and molecular-scale structure of the sample.
Geometry
We define a vector in reciprocal-space as the difference between the incident and scattered x-ray beams. This new vector is the momentum transfer, denoted by q:
The length of this vector is:
Theory
The mathematical form of scattering is closely related to the Fourier transform. The sample's realspace density distribution is Fourier transformed into an abstract 3D reciprocal-space; scattering probes this inverse space.

