Difference between revisions of "Form Factor:Superball"
KevinYager (talk | contribs) (→Mathematical descriptions of superballs) |
KevinYager (talk | contribs) (→References) |
||
| Line 39: | Line 39: | ||
====Application to nanoscience==== | ====Application to nanoscience==== | ||
* Yugang Zhang, Fang Lu, Daniel van der Lelie, Oleg Gang "[http://prl.aps.org/abstract/PRL/v107/i13/e135701 Continuous Phase Transformation in Nanocube Assemblies]" ''Physical Review Letters'' '''2011''', 107, 135701 [http://dx.doi.org/10.1103/PhysRevLett.107.135701 doi: 10.1103/PhysRevLett.107.135701] | * Yugang Zhang, Fang Lu, Daniel van der Lelie, Oleg Gang "[http://prl.aps.org/abstract/PRL/v107/i13/e135701 Continuous Phase Transformation in Nanocube Assemblies]" ''Physical Review Letters'' '''2011''', 107, 135701 [http://dx.doi.org/10.1103/PhysRevLett.107.135701 doi: 10.1103/PhysRevLett.107.135701] | ||
| + | |||
| + | ====Use in scattering==== | ||
| + | * [[Yager, K.G.]]; Zhang, Y.; Lu, F.; Gang, O. "[http://scripts.iucr.org/cgi-bin/paper?S160057671302832X Periodic lattices of arbitrary nano-objects: modeling and applications for self-assembled systems]" ''Journal of Applied Crystallography'' '''2014''', 47, 118–129. [http://dx.doi.org/0.1107/S160057671302832X doi: 10.1107/S160057671302832X] | ||
Revision as of 10:35, 20 January 2015
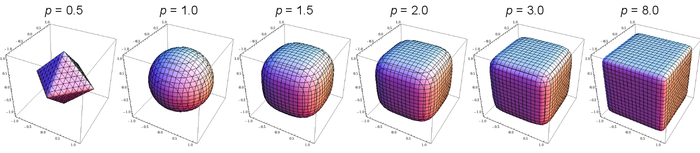
A superball is a general mathematical shape that can be used to describe rounded cubes. In fact, it is a general parametrization that can describe, via a parameter :
- Empty space ()
- Concave octahedra ()
- Octahedra ()
- Convex octahedra ()
- Spheres ()
- Rounded cubes ()
- Cubes ()
The general equation is parametrized by the size, , and the curvature :
Obviously for , we recover the equation for a sphere. In the limit of large , we obtain a cube.
Contents
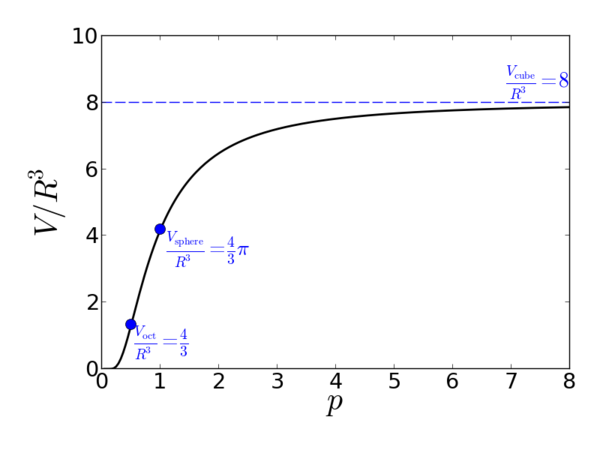
Volume
The normalized volume for a superball is:
Where and is the usual Euler gamma function.
Equations
The form factor for a superball is likely not analytic. However, it can be computed numerically.
References
Mathematical descriptions of superballs
- N. D. Elkies, A. M. Odlyzko and J. A. Rush "On the packing densities of superballs and other bodies" Inventiones Mathematicae Volume 105, Number 1 (1991), 613-639, doi: 10.1007/BF01232282
- Y. Jiao, F.H. Stillinger, S. Torquato "Optimal packings of superballs" Physical Review E 2009, 79, 041309, doi: 10.1103/PhysRevE.79.041309
Application to nanoscience
- Yugang Zhang, Fang Lu, Daniel van der Lelie, Oleg Gang "Continuous Phase Transformation in Nanocube Assemblies" Physical Review Letters 2011, 107, 135701 doi: 10.1103/PhysRevLett.107.135701
Use in scattering
- Yager, K.G.; Zhang, Y.; Lu, F.; Gang, O. "Periodic lattices of arbitrary nano-objects: modeling and applications for self-assembled systems" Journal of Applied Crystallography 2014, 47, 118–129. doi: 10.1107/S160057671302832X