Reflectivity

Reflectivity refers to the measurement of the intensity of reflection off of a flat interface. The term both describes the physical phenomenon, as well as the experimental technique.

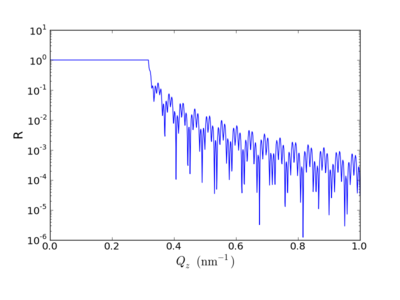
X-ray Reflectivity (XRR or XR) and neutron reflectivity (NR) are techniques which measure the intensity of reflected radiation as a function of angle (where, by definition for specular reflectivity, the incident and exit angles are equal; $\scriptstyle \theta _{i}=\theta _{f}$). A plot of reflectivity (R) versus angle yields the reflectivity curve. For XR and NR, the data is typically plotted as a function of the momentum transfer parallel to the film normal:

$q_{z}={\frac {4\pi }{\lambda }}\sin \theta$

Reflectivity calculation for a thin film.

Off-Specular Reflectivity

TBD

Mathematical form

In its simplest form, the Fresnel reflectivity can be given by:

$R_{F}={\frac {k_{z}-{\tilde {k}}_{z}}{k_{z}+{\tilde {k}}_{z}}}$

Where:

${\tilde {k}}_{z}=-{\sqrt {n^{2}k_{0}^{2}-|k_{\parallel }|^{2}}}$

And n is the complex refractive index of the substrate. The idealized uncorrelated roughness can be characterized by a mean standard deviation of the height $\scriptstyle \sigma ={\sqrt {\left\langle h^{2}\right\rangle }}$:

$R_{S}=R_{F}e^{-2\sigma ^{2}k_{z}{\tilde {k}}_{z}}$

For a substrate with a single continuous layer of thickness h (e.g. a uniform thin film), the reflectivity becomes:

$R_{S}={\frac {r_{01}+r_{12}e^{2i{\tilde {k}}_{z}^{1}h}}{1+r_{01}r_{12}e^{2i{\tilde {k}}_{z}^{1}h}}}$

where Failed to parse (syntax error): {\displaystyle \tilde{k}^j_z=-\sqrt(n^2_j k^2_0 - |k_{\parallel}|^2 }} is the perpendicular component of the wave-vector (in medium j). The reflectivity coefficients are:

$f_{ij}={\frac {{\tilde {k}}_{z}^{i}-{\tilde {k}}_{z}^{j}}{{\tilde {k}}_{z}^{i}+{\tilde {k}}_{z}^{j}}}$

Where $\scriptstyle r_{01}$ and $\scriptstyle r_{12}$ for the vacuum-layer and layer-substrate interfaces, respectively. This is called the 'one-box model'.

Parratt formalism

TBD

See Also

• Fresnel plot
• Oscillations below the critical angle
• DWBA: A formalism for modeling GISAXS data, including reflection effects.