Grating alignment
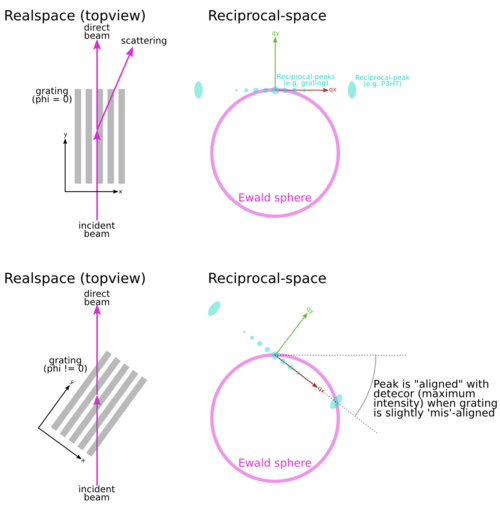
In order to align a lithographic (nanoscale) grating with the incident x-ray beam, one must rotate it carefully about the axis (i.e. the film normal direction) until the grating lines are exactly parallel to the incident beam. If the grating is not aligned, the scattering spots seen in GISAXS will not be symmetric.
Aligning
If the
Origin of Ring
The "ring" of bright scattering spots that one observes arises from the intersection of the Ewald sphere with the reciprocal lattice. Because lithographic gratings are so well-ordered, the reciprocal-space peaks are extremely sharp. Thus, the scattering intensity is strongly concentrated into the plane. The curved Ewald sphere intersects this plane to give rise to a circle of intense scattering.
One can perform a 'phi rock': where one integrates the detector signal as the sample is rotated about the axis. This sweeps the Ewald sphere through reciprocal-space, effectively accumulating all the intensity that is along the plane in reciprocal-space. The end result is that the detector image includes the full array of diffraction peaks.
Grating with material
Lithographic gratings are often used to align other materials (small molecules, block-copolymers, semiconducting polymers, etc.). When assessing scattering data arising from such systems, one must be careful to correctly interpret the 'aligned' direction.
Let's say you align the grating at phi=0. There is a peak in reciprocal space at fairly large |q| (let's say the P3HT 100). Normally we would say that if you see this peak on the detector when phi=0, then we can say the P3HT is aligned with phi=0. However, this isn't quite right because of the curvature of the Ewald sphere. If the peak is truly aligned with the grating, then the peak on the detector will be maximized when we slightly offset phi, by just enough to counter-act the size of the Bragg angle.
Another way to think about it is to say that if you rotate your grating, and some peak is maximized at phi=gamma degrees, then you shouldn't really say "sample has maximum alignment at gamma", but actually "sample has maximum alignment at (gamma-correction)", where you calculation the correction based on the geometry, Bragg angle, etc.
See Also
- Direct structural characterisation of line gratings with grazing incidence small-angle x-ray scattering Jan Wernecke, Frank Scholze, Michael Krumrey Rev. Sci. Instrum. 2012, 83, 103906 doi: 10.1063/1.4758283
- On the assessment by grazing-incidence small-angle X-ray scattering of replica quality in polymer gratings fabricated by nanoimprint lithography M. Soccio, N. Alayo, I. Martín-Fabiani, D. R. Rueda, M. C. García-Gutiérrez, E. Rebollar, D. E. Martínez-Tong, F. Pérez-Murano and T. A. Ezquerra J. Appl. Cryst. 2014, 47, 613-618 doi: 10.1107/S160057671400168X