DWBA
The Distorted Wave Born Approximation (DWBA) is a theoretical approach in scattering theory (or, more generally, in quantum mechanics). In the Born approximation (BA), when calculating the interaction between matter and incident radiation ('scattering'), the total field inside the material is assumed to simply be the incident field. In other words, the modification of the field due to scattering events is assumed to be negligible; this is valid in the limit of weak scattering. Every particle simply sees the incident field, and scatters independently (though these scattered fields interfere with one another, giving rise to the usual appearance of scattering features in the far-field).
The Born approximation is not valid in all cases; in particular, when scattering becomes very strong, the approximation is no longer valid. As one example, at some point one must consider multiple scattering: the scattered rays can, themselves, become sources of scattering. GISAXS and other grazing-incidence techniques typically probe regimes where the Born approximation is not valid. For instance, in GISAXS, the x-ray beam will be reflected by the film-substrate and film-ambient interfaces; and may in fact undergo multiple reflections (waveguiding). This, and other dynamical scattering effects need to be accounted for in order to understand GISAXS data.
The DWBA is an extension to the BA, which accounts for higher-order multiple scattering effects. Conceptually, it accounts for the fact that the radiation field in the material should be solved under the condition that the scattering entities introduce substantial perturbations to the field. Mathematically, DWBA uses the BA as an idealized case, to which successive perturbation terms are introduced.
Contents
Mathematical form
In the simplest DWBA formalism, the sample is assumed to be a flat interface, with perturbations thereof that encode the in-plane order (lateral electron-density distribution). The sample's structure can also be thought of as a variety of nanoscale scattering objects distributed over an otherwise flat substrate. As usual, the scattering intensity can be split into a Form Factor and Structure Factor contribution:
The structure factor (S) describes the spatial arrangement of the objects (Fourier transform of the position autocorrelation function), while the form factor (F) is the Fourier transform of the shape of the objects. In the BA, this simply:
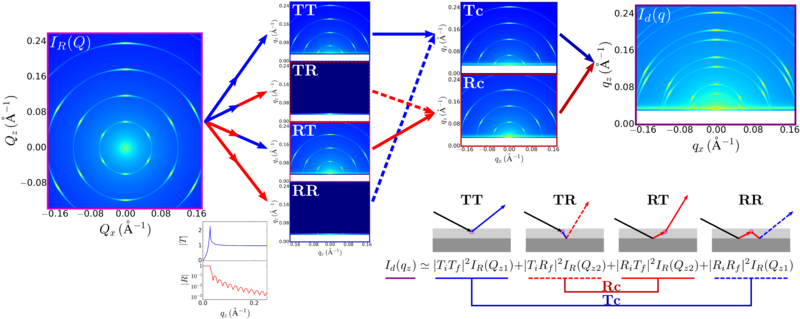
However, to account for reflection and refraction effects, the DWBA introduces additional terms. The figure below shows four different scattering events which are considered:
The first term is the BA, while the next 3 terms describe various specific multiple-scattering events. In principle, an infinite series of different combinations of reflection and scattering need to be included. However, as will be seen, higher-order terms are progressively more and more unlikely (and thus weak, in terms of their contribution to the total scattering). The DWBA, by considering these 4 terms, can adequately reproduce much GISAXS data. The various terms described above interfere coherently; thus the final scattering that is measured on the detector comes from their combination:
It is important to notice that the higher-order contributions to F are multiplied by the Fresnel reflectivity (). This occurs since these terms involve reflection events.
Where:
And n is the complex refractive index of the substrate.
Because the reflectivity falls off very rapidly with increasing angle (scaling of ), these terms are only relevant at small angles. This has several implications:
- The DWBA is only relevant at small incident angles (); i.e. it matters for grazing-incidence experiments, but not transmission scattering (TSAXS).
- The DWBA is only relevant at small exit angles (); i.e. it matters for GISAXS but not GIWAXS, and is most pronounced at small angles (near the Yoneda and horizon).
- Higher-order terms (beyond the 4 covered by the DWBA) are strongly suppressed because they involve even more multiplications by . These can thus be ignored, except when angles are very close to the critical angle (e.g. x-ray waveguiding).
Using the effective form factor (), the total incoherent cross-section becomes:
While the coherent cross-section accounts for the specular rod.
Channels
The DWBA has four scattering terms, which can conceptually be divided into two channels: transmission channel (scattering direction consistent with incident beam) and reflection channel (scattering consistent with reflected beam).
References
Foundational
- George H. Vineyard Grazing-incidence diffraction and the distorted-wave approximation for the study of surfaces Phys. Rev. B 1982, 26, 4146. doi: 10.1103/PhysRevB.26.4146
- S. K. Sinha, E. B. Sirota, S. Garoff, and H. B. Stanley X-ray and neutron scattering from rough surfaces Phys. Rev. B 1988, 38, 2297. doi: 10.1103/PhysRevB.38.2297
- M. Rauscher, T. Salditt, and H. Spohn Small-angle x-ray scattering under grazing incidence: The cross section in the distorted-wave Born approximation Phys. Rev. B 1995, 52, 16855. doi: 10.1103/PhysRevB.52.16855
- Michael F. Toney and Sean Brennan Observation of the effect of refraction on x rays diffracted in a grazing-incidence asymmetric Bragg geometry Phys. Rev. B 1989, 39, 7963. doi: 10.1103/PhysRevB.39.7963
Variants
- Islands on surfaces:
- Markus Rauscher, Rogerio Paniago, Hartmut Metzger, Zoltan Kovats, Jan Domke, Johann Peisl, Hans-Dieter Pfannes, Jörg Schulze and Ignaz Eisele Grazing incidence small angle x-ray scattering from free-standing nanostructures J. Appl. Phys. 1999, 86, 6763. doi: 10.1063/1.371724
- R. Lazzari IsGISAXS: a program for grazing-incidence small-angle X-ray scattering analysis from supported islands J. Appl. Cryst. 2002, 35, 406-421. doi: 10.1107/S0021889802006088
- Graded interface:
- Dick K. G. de Boer X-ray scattering and x-ray fluorescence from materials with rough interfaces Phys. Rev. B 1996, 53, 6048. doi: 10.1103/PhysRevB.53.6048
- A. Sentenac and J.-J. Greffet Mean-field theory of light scattering by one-dimensional rough surfaces JOSA A 1998, 15 (2), 528-532. doi: 10.1364/JOSAA.15.000528
- Rémi Lazzari, Frédéric Leroy, and Gilles Renaud Grazing-incidence small-angle x-ray scattering from dense packing of islands on surfaces: Development of distorted wave Born approximation and correlation between particle sizes and spacing Phys. Rev. B 2007, 76, 125411. doi: 10.1103/PhysRevB.76.125411
- X-ray waveguiding: Zhang Jiang, Dong Ryeol Lee, Suresh Narayanan, Jin Wang, and Sunil K. Sinha Waveguide-enhanced grazing-incidence small-angle x-ray scattering of buried nanostructures in thin films Phys. Rev. B 2011, 84, 075440. doi: 10.1103/PhysRevB.84.075440
Refraction Correction
- Byeongdu Lee, Insun Park, Jinhwan Yoon, Soojin Park, Jehan Kim, Kwang-Woo Kim, Taihyun Chang, and Moonhor Ree Structural Analysis of Block Copolymer Thin Films with Grazing Incidence Small-Angle X-ray Scattering Macromolecules 2005, 38 (10), 4311-4323. doi: 10.1021/ma047562d
- P. Busch, M. Rauscher, D.-M. Smilgies, D. Posselt and C. M. Papadakis Grazing-incidence small-angle X-ray scattering from thin polymer films with lamellar structures - the scattering cross section in the distorted-wave Born approximation J. Appl. Cryst. 2006, 39, 433-442. doi: 10.1107/S0021889806012337
- Rémi Lazzari, Frédéric Leroy, and Gilles Renaud Grazing-incidence small-angle x-ray scattering from dense packing of islands on surfaces: Development of distorted wave Born approximation and correlation between particle sizes and spacing Phys. Rev. B 2007, 76, 125411. doi: 10.1103/PhysRevB.76.125411
- D. W. Breiby, O. Bunk, J. W. Andreasen, H. T. Lemke and M. M. Nielsen Simulating X-ray diffraction of textured films J. Appl. Cryst. 2008, 41, 262-271. doi: 10.1107/S0021889808001064
- Lu, X.; Yager, K.G.; Johnston, D.; Black, C.T.; Ocko, B.M. Grazing-incidence transmission X-ray scattering: surface scattering in the Born approximation Journal of Applied Crystallography 2013, 46, 165–172. doi: 10.1107/S0021889812047887
- Liu, J.; Yager, K.G. Unwarping GISAXS data IUCrJ 2018, 5, 737–752. doi: 10.1107/S2052252518012058
Multiple Channels
- Byeongdu Lee, Insun Park, Jinhwan Yoon, Soojin Park, Jehan Kim, Kwang-Woo Kim, Taihyun Chang, and Moonhor Ree Structural Analysis of Block Copolymer Thin Films with Grazing Incidence Small-Angle X-ray Scattering Macromolecules 2005, 38 (10), 4311–4323. doi: 10.1021/ma047562d
- Liu, J.; Yager, K.G. Unwarping GISAXS data IUCrJ 2018, 5, 737–752. doi: 10.1107/S2052252518012058
Application of DWBA
- Nanoporous thin film: Byeongdu Lee, Jinhwan Yoon, Weontae Oh, Yongtaek Hwang, Kyuyoung Heo, Kyeong Sik Jin, Jehan Kim, Kwang-Woo Kim and Moonhor Ree In-Situ Grazing Incidence Small-Angle X-ray Scattering Studies on Nanopore Evolution in Low-k Organosilicate Dielectric Thin Films Macromolecules 2005, 38 (8), 3395–3405 doi: 10.1021/ma048214e
- Lamellar mesostructures: P. Busch, M. Rauscher, D.-M. Smilgies, D. Posselt and C. M. Papadakis Grazing-incidence small-angle X-ray scattering from thin polymer films with lamellar structures - the scattering cross section in the distorted-wave Born approximation J. Appl. Cryst. 2006, 39, 433-442. doi: 10.1107/S0021889806012337
- Diffraction patterns: Tate MP, Urade VN, Kowalski JD, Wei TC, Hamilton BD, Eggiman BW, Hillhouse HW Simulation and interpretation of 2D diffraction patterns from self-assembled nanostructured films at arbitrary angles of incidence: from grazing incidence (above the critical angle) to transmission perpendicular to the substrate J. Phys. Chem. B 2006, 110 (20), 9882–9892. doi: 10.1021/jp0566008
- Ge nanodots: H Okuda, K Kuno, S Ochiai, N Usami, K Nakajima, O Sakata, S Sasaki and M Takata Effect of reflected waves on the GISAXS analysis of as-grown capped Ge nanodots J. Phys.: Conf. Ser. 2009, 184, 012005. doi: 10.1088/1742-6596/184/1/012005
Summaries/Reviews
- Gilles Renaud, Rémi Lazzari, Frédéric Leroy Probing surface and interface morphology with Grazing Incidence Small Angle X-Ray Scattering Surface Science Reports 2009 64 (8), 255-380. doi: 10.1016/j.surfrep.2009.07.002