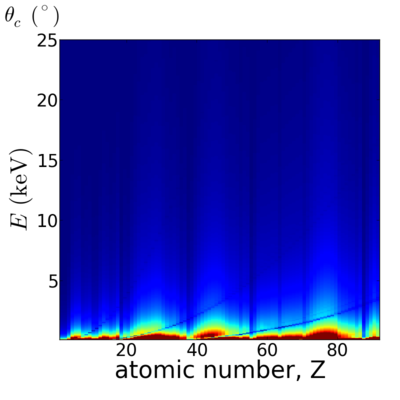
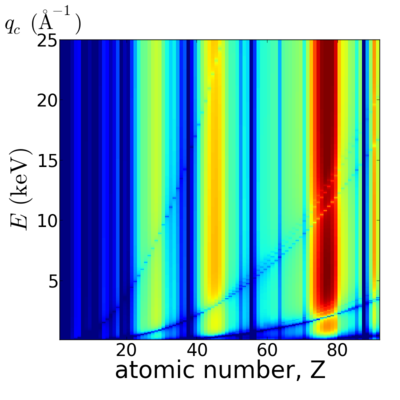
Critical angle

In GISAXS, the critical angle for a thin film is the incident angle below which one gets total external reflection of the x-ray beam.

Below the critical angle, the beam is fully reflected from the film. The x-ray field probes a short distance into the film surface (due to the evanescent wave); on the order of a few nanometers. Thus, a GISAXS measurement below the critical angle is inherently probing only the film surface. A measurement well above the critical angle, by comparison, penetrates through the film and thus measures the average of the structure through the whole film. Close to the critical angle, the refracted beam is nearly parallel to the film interface; in other words the beam is coupled into waveguide modes. This increases the effective path-length of the beam through the sample, which thereby increases the intensity of the scattering.

Normally in GISAXS experiments, it is useful to do measurements both below and above the critical angle; by comparing the two patterns, you can ascertain whether the structures observed at the surface (e.g. as seen by AFM or SEM) are representative of the entire film. Measurements close to the critical angle are useful because of the intensity enhancement.

Examples

Material	density (g/cm³)	X-ray energy (keV)	X-ray wavelength (Å)	critical angle (°)	q_c (Å⁻¹)	SLD (10⁻⁶Å⁻²)
polystyrene	1.00	2.0	6.20	0.613	0.0217	9.34
		4.0	3.10	0.304	0.0215	9.21
		8.0	1.55	0.152	0.0214	9.15
		12.0	1.03	0.101	0.0214	9.13
		16.0	0.77	0.076	0.0214	9.13
		24.0	0.52	0.050	0.0214	9.12

Material	density (g/cm³)	X-ray energy (keV)	X-ray wavelength (Å)	critical angle (°)	q_c (Å⁻¹)	SLD (10⁻⁶Å⁻²)
Si	2.3290	2.0	6.20	0.824	0.0291	16.89
		4.0	3.10	0.451	0.0319	20.28
		8.0	1.55	0.224	0.0317	20.07
		12.0	1.03	0.149	0.0317	19.92
		16.0	0.77	0.112	0.0316	19.84
		24.0	0.52	0.07426	0.0315	19.77

Material	density (g/cm³)	X-ray energy (keV)	X-ray wavelength (Å)	critical angle (°)	q_c (Å⁻¹)	SLD (10⁻⁶Å⁻²)
SiO2	2.648	2.0	6.20	0.927	0.0328	21.42
		4.0	3.10	0.480	0.0340	22.96
		8.0	1.55	0.239	0.0338	22.71
		12.0	1.03	0.159	0.0337	22.58
		16.0	0.77	0.119	0.0337	22.53
		24.0	0.52	0.079	0.0336	22.48

Material	density (g/cm³)	X-ray energy (keV)	X-ray wavelength (Å)	critical angle (°)	q_c (Å⁻¹)	SLD (10⁻⁶Å⁻²)
Au	19.32	2.0	6.20	1.830	0.0647	83.44
		4.0	3.10	1.097	0.0776	119.89
		8.0	1.55	0.560	0.0792	124.86
		12.0	1.03	0.348	0.0738	108.29
		16.0	0.77	0.282	0.0797	126.51
		24.0	0.52	0.191	0.0811	130.80

Critical q

The critical angle can be converted into a critical momentum transfer. In reflection-mode, the scattering vector is:

{\begin{alignedat}{2}\mathbf {q} &=\mathbf {k} _{o}-\mathbf {k} _{i}\\|\mathbf {q} |&=q=2|k|\sin \theta _{i}={\frac {4\pi }{\lambda }}\sin \theta _{i}\end{alignedat}}

Where λ is the wavelength of the x-rays. So, the critical q in reciprocal-space is:

q_{c}={\frac {4\pi }{\lambda }}\sin \theta _{c}

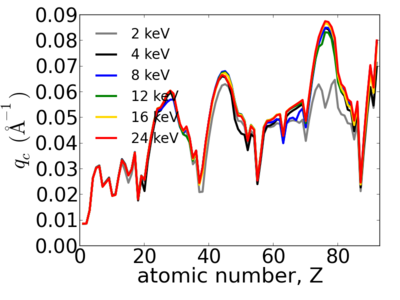
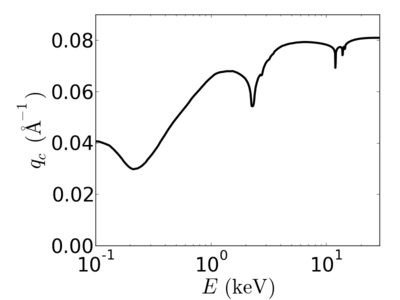
The critical q somewhat factors-out the influence of x-ray energy, making q_c less sensitive to variations in energy. However, even q_c strictly has an energy-dependence.

Calculating

The critical angle for a material can be calculated in a variety of ways. For an elemental substance, this online tool will calculate it for you.

From SLD

The Scattering Length Density (SLD) for any given material can be computed using tabulated values. From this, the critical angle can be computed. The critical scattering vector is:

q_{c}={\sqrt {16\pi \mathrm {SLD} }}

So:

{\begin{alignedat}{2}\theta _{c}&=\arcsin \left({\frac {q_{c}\lambda }{4\pi }}\right)\\&=\arcsin \left({\frac {\lambda {\sqrt {16\pi \mathrm {SLD} }}}{4\pi }}\right)\\&\approx {\sqrt {\frac {\lambda ^{2}\mathrm {SLD} }{\pi }}}\end{alignedat}}

From refractive index

The critical angle is simply a result of the refractive index contrast between the film and the ambient. Of course, in this case we are talking about the x-ray refractive index (not the usual refractive index for visible light). In the case of neutrons, the film similarly exhibits a neutron refractive index. The refractive index is complex:

n=1-\delta +i\beta

For x-rays, the values of 𝛿 and β can be calculated from the atomic scattering factors (f₁ and f₂) using:

\delta ={\frac {n_{a}r_{e}\lambda ^{2}}{2\pi }}f_{1}

\beta ={\frac {n_{a}r_{e}\lambda ^{2}}{2\pi }}f_{2}

Where r_e is the classical electron radius (2.8179403x10⁻¹⁵ m), λ is the wavelength of the probing x-rays, and n_a is the number density:

n_{a}={\frac {\rho N_{a}}{M_{a}}}

where ρ is the physical density (e.g. in g/cm³), N_a is the Avogadro constant (6.02214129x10²³ mol⁻¹), and M_a is molar mass (e.g. in g/mol). There are also online tools that will compute the refractive index for you.

Once the real part of the refractive index (𝛿) is known, conversion to critical angle is straightforward:

\theta _{c}={\sqrt {2\delta }}

Note that the resultant critical angle has units of radians. For a multi-component system, one simply uses a weighted sum of the contributions from each element:

\theta _{c}={\sqrt {\frac {\rho N_{a}r_{e}\lambda ^{2}\sum _{i=1}^{N}c_{i}f_{1i}}{\pi \sum _{i=1}^{N}c_{i}M_{i}}}}

where the c_i the weighting factors (concentration, or stoichiometric numbers in a chemical formula).

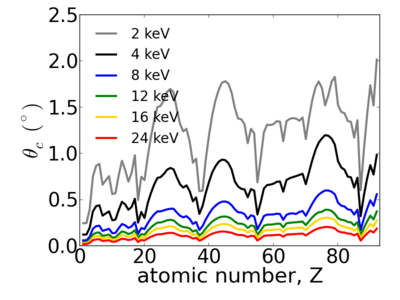
Elemental dependence

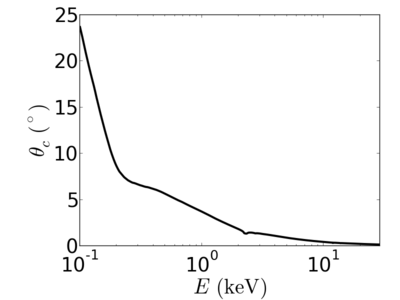
Energy dependence

The critical angle depends on the real part of the refractive index. In general, high-energy (short wavelength) x-rays are more weakly refracted, giving rise to a smaller critical angle.