Atomic scattering factors
The atomic scattering factors are measures of the scattering power of individual atoms. Each element has a different atomic scattering factor, which represents how strongly x-rays interact with those atoms.
The scattering factor has two components: f1 and f2, which describe the dispersive and absorptive components. In other words, f2 describes how strongly the material absorbs the radiation, while f1 describes the non-absorptive interaction (which leads to refraction).
Contents
Elemental dependence
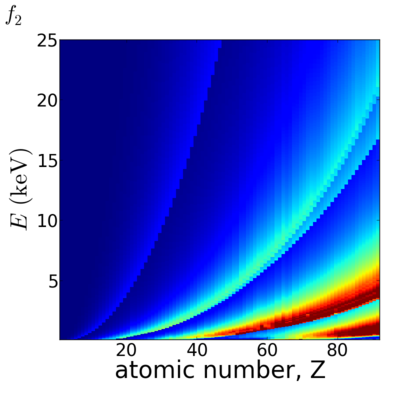
Because x-ray interactions occur with an atom's electron cloud, the scattering factors increase with number of electrons, and thus with atomic number (Z). However, the relationship between f and Z is not monotonic, owing to resonant (absorption) edges.
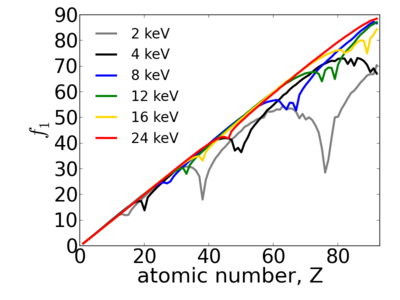
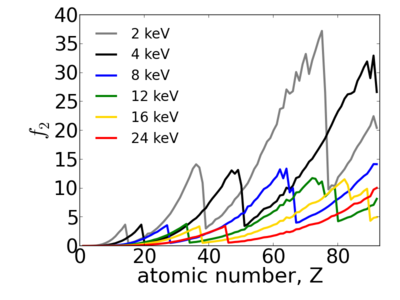
Energy dependence
The atomic scattering factors vary with x-ray wavelength. In particular, a given element will have resonant edges at certain energies, where the absorption increases markedly. The dispersive component f1 will also vary rapidly in the vicinity of an absorption edge (c.f. Kramers-Kronig relations). In general, absorption decreases with increasing energy (i.e. high-energy x-rays can penetrate more efficiently through materials).
Examples
silicon
gold
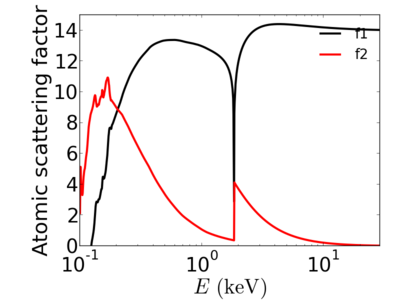
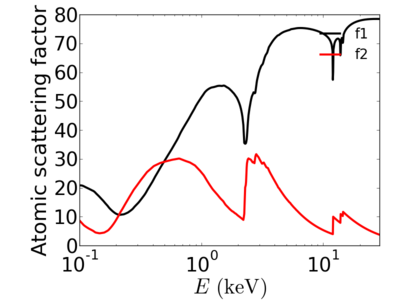
Elemental/Energy dependence
Related forms
There are a variety of quantities related to the material's x-ray interaction strength:
- Dispersive atomic scattering factor Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_1} , the intrinsic interaction of the material.
- Critical angle Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_c} , the angle below which the beam undergoes total external reflection.
- Critical wave-vector Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_c} , the momentum transfer (in reciprocal-space) corresponding to the critical angle.
- Real refractive index Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} , the refractive component of the refractive index.
- Real Scattering Length Density Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{Re}(\mathrm{SLD})} , the primary (non-absorptive) component of the scattering contrast.
- Electron Density Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_e} , the number of electrons per unit volume.
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_1} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_1 = \frac{ \pi M_a}{ \rho N_a r_e \lambda^2 } \theta_c^2} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_1 = \frac{ M_a}{ 16 \pi \rho N_a r_e } q_c^2} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_1 = \frac{2 \pi M_a}{ \rho N_a r_e \lambda^2 } \delta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_1 = \frac{M_a}{\rho N_a r_e} \mathrm{Re}(\mathrm{SLD}) } | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_1 = \frac{M_a}{\rho N_a} \rho_e} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_c = \sqrt{ \frac{ \rho N_a r_e \lambda^2 }{ \pi M_a} f_1 }} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_c} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_c \approx \frac{\lambda}{4 \pi} q_c } | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_c = \sqrt{ 2 \delta }} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_c\approx \sqrt{\frac{\lambda^2 \mathrm{SLD} }{\pi}}} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_c = \sqrt{ \frac{r_e \lambda^2}{\pi} \rho_e }} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_c = \sqrt{ \frac{ 16 \pi \rho N_a r_e }{ M_a} f_1 }} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_c = \frac{4 \pi}{\lambda}\sin\theta_c} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_c} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_c \approx \frac{4\pi}{\lambda}\sqrt{ 2\delta }} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_c = \sqrt{ 16 \pi \mathrm{SLD} }} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_c = 4 \sqrt{ \pi r_e \rho_e}} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta = \frac{ \rho N_a r_e \lambda^2 }{2 \pi M_a} f_1} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta = \frac{\theta_c^2}{2}} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta \approx \frac{\lambda^2}{32 \pi^2}q_c^2} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta \approx \frac{\lambda^2}{2 \pi}\mathrm{Re}(\mathrm{SLD})} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta = \frac{\lambda^2 r_e}{2 \pi} \rho_e} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{Re}(\mathrm{SLD}) = \frac{\rho N_a r_e}{M_a} f_1} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{Re}(\mathrm{SLD}) \approx \frac{\pi}{\lambda^2}\theta_c^2} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{Re}(\mathrm{SLD}) = \frac{q_c^2}{16\pi}} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{Re}(\mathrm{SLD}) \approx \frac{2 \pi}{\lambda^2}\delta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{Re}(\mathrm{SLD})} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{Re}(\mathrm{SLD}) = r_e \rho_e} |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_e = \frac{\rho N_a}{M_a} f_1} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_e = \frac{\pi}{r_e \lambda^2} \theta_c^2} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_e = \frac{q_c^2}{ 16 \pi r_e }} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_e = \frac{2 \pi}{r_e \lambda^2} \delta} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_e = \frac{ \mathrm{Re}(\mathrm{SLD}) }{r_e}} | Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \rho_e} |
See also absorption length for a comparison of the quantities related to f2.
See Also
- Atomic Form Factor
- Periodic table of atomic scattering factors: Useful tool for looking up the values for any element.
- APS Python code for calculating f
- Online Dictionary of Crystallography: Atomic scattering factor
