The absorption length or attenuation length in x-ray scattering is the distance over which the x-ray beam is absorbed. By convention, the absorption length ϵ is defined as the distance into a material where the beam flux has dropped to 1/e of its incident flux.
Absorption
The absorption follows a simple Beer-Lambert law:

The attenuation coefficient (or absorption coefficient) is simply the inverse of the absorption length; 

Calculating
The absorption length arises from the imaginary part of the atomic scattering factor, f2. It is closely related to the absorption cross-section, and the mass absorption coefficient. Specifically, the atomic photoabsorption cross-section can be computed via:

Where λ is the x-ray wavelength, and re is the classical electron radius. The attenuation coefficient is given by:

where ρ is density, Na is the Avogadro constant, and ma is the atomic molar mass. Note that the mass attenuation coefficient is simply  .
.
Elemental dependence

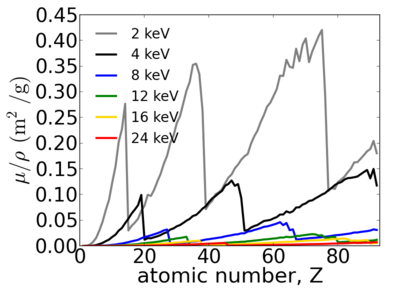
Energy dependence
Notice that the absorption undergoes sharp increases when passing through an absorption edge.
Examples
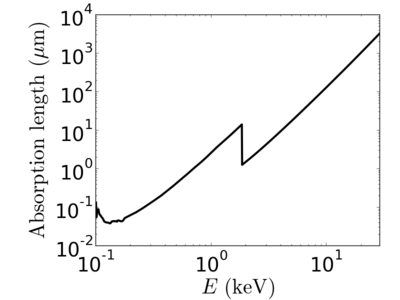
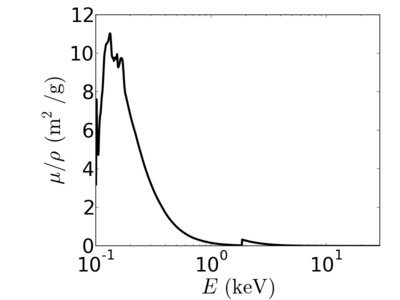
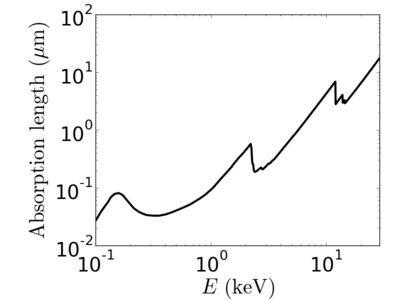
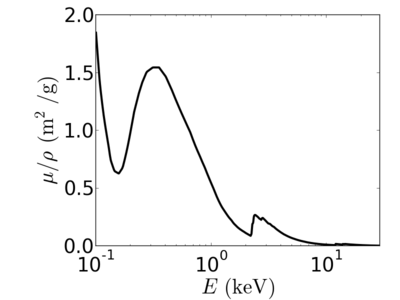
Elemental/Energy dependence
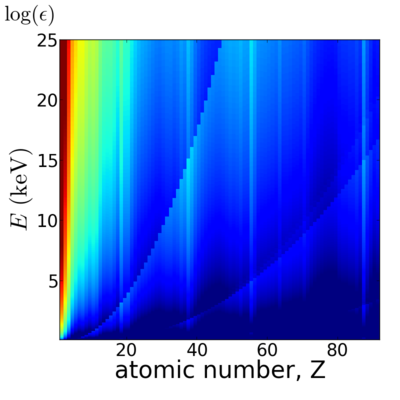

Related forms
As can be seen, there are many related quantities which express the material's absorption:
- Absorption length
 , the distance over which the intensity falls to 1/e.
, the distance over which the intensity falls to 1/e.
- Attenuation coefficient
 , the characteristic inverse-distance for attenuation.
, the characteristic inverse-distance for attenuation.
- Mass attenuation coefficient
 , the density-scaled attenuation.
, the density-scaled attenuation.
- Absorptive atomic scattering factor
 , the intrinsic dissipative interaction of the material.
, the intrinsic dissipative interaction of the material.
- Atomic photoabsorption cross-section
 , the cross-section ('effective size') of the atom's x-ray absorption (capture) efficiency.
, the cross-section ('effective size') of the atom's x-ray absorption (capture) efficiency.
- Imaginary refractive index
 , the resonant component of the refractive index.
, the resonant component of the refractive index.
- Imaginary Scattering Length Density
 , the absorptive component of the scattering contrast.
, the absorptive component of the scattering contrast.

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
See also scattering factors for a comparison of the quantities related to f1.
See Also



























































