The atomic scattering factors are measures of the scattering power of individual atoms. Each element has a different atomic scattering factor, which represents how strongly x-rays interact with those atoms.
The scattering factor has two components: f1 and f2, which describe the dispersive and absorptive components. In other words, f2 describes how strongly the material absorbs the radiation, while f1 describes the non-absorptive interaction (which leads to refraction).
Elemental dependence
Because x-ray interactions occur with an atom's electron cloud, the scattering factors increase with number of electrons, and thus with atomic number (Z). However, the relationship between f and Z is not monotonic, owing to resonant (absorption) edges.
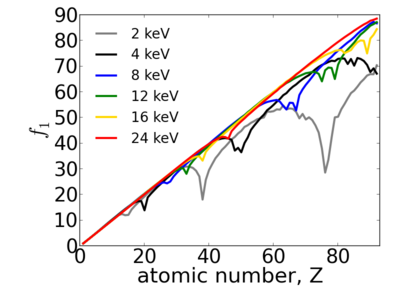
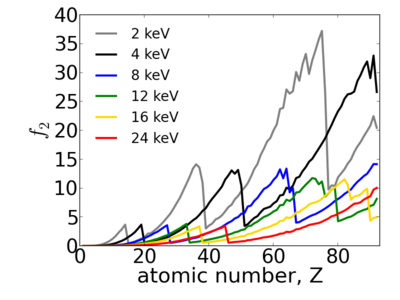
Energy dependence
The atomic scattering factors vary with x-ray wavelength. In particular, a given element will have resonant edges at certain energies, where the absorption increases markedly. The dispersive component f1 will also vary rapidly in the vicinity of an absorption edge (c.f. Kramers-Kronig relations). In general, absorption decreases with increasing energy (i.e. high-energy x-rays can penetrate more efficiently through materials).
Examples
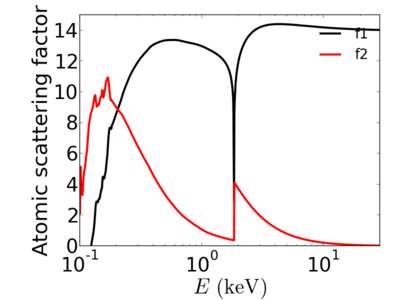
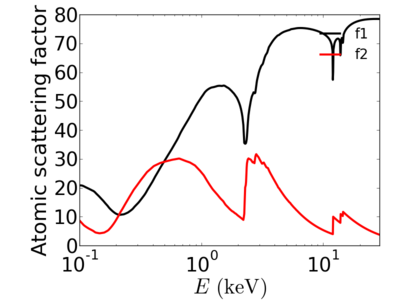
Elemental/Energy dependence
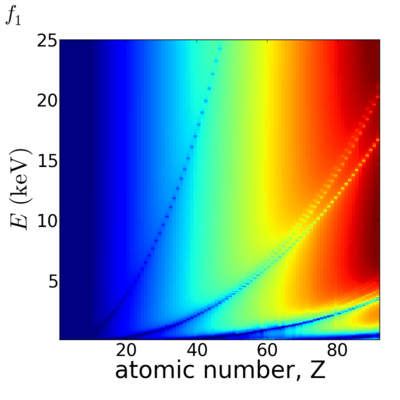
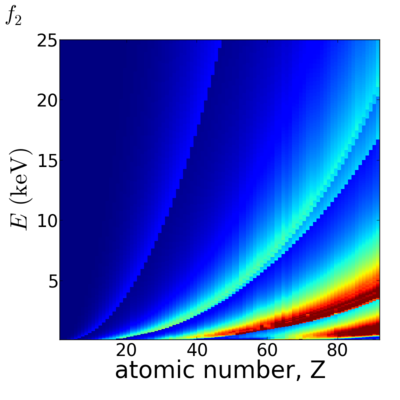
Related forms
There are a variety of quantities related to the material's x-ray interaction strength:

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
See also absorption length for a comparison of the quantities related to f2.
See Also








































