Difference between revisions of "Reflectivity"
KevinYager (talk | contribs) (→Parratt formalism) |
KevinYager (talk | contribs) |
||
| Line 3: | Line 3: | ||
'''[[X-ray]] Reflectivity''' ('''XRR''' or '''XR''') and '''[[neutron]] reflectivity''' ('''NR''') are techniques which measure the intensity of reflected radiation as a function of angle (where, by definition for '''specular reflectivity''', the incident and exit angles are equal; <math>\scriptstyle \theta_i = \theta_f</math>). A plot of reflectivity (''R'') versus angle yields the '''reflectivity curve'''. For XR and NR, the data is typically plotted as a function of the [[momentum transfer]] parallel to the film normal: | '''[[X-ray]] Reflectivity''' ('''XRR''' or '''XR''') and '''[[neutron]] reflectivity''' ('''NR''') are techniques which measure the intensity of reflected radiation as a function of angle (where, by definition for '''specular reflectivity''', the incident and exit angles are equal; <math>\scriptstyle \theta_i = \theta_f</math>). A plot of reflectivity (''R'') versus angle yields the '''reflectivity curve'''. For XR and NR, the data is typically plotted as a function of the [[momentum transfer]] parallel to the film normal: | ||
:<math> | :<math> | ||
| − | q_z = \frac{4\pi}{\lambda} \sin \ | + | q_z = \frac{4\pi}{\lambda} \sin \theta_i |
</math> | </math> | ||
| Line 12: | Line 12: | ||
==Mathematical form== | ==Mathematical form== | ||
| + | ===Ideal interface=== | ||
In its simplest form, the Fresnel reflectivity can be given by: | In its simplest form, the Fresnel reflectivity can be given by: | ||
:<math> | :<math> | ||
| − | + | r_F = \frac{k_z-\tilde{k}_z}{k_z+\tilde{k}_z} | |
</math> | </math> | ||
| − | Where: | + | Where <math>\scriptstyle k_z</math> is the vertical (''z'') component of the momentum of the incident wave, and <math>\scriptstyle \tilde{k}_z</math> is the vertical component of the transmitted wave: |
:<math> | :<math> | ||
\tilde{k}_z = - \sqrt{ n^2 k^2_0 - |k_{\parallel}|^2 } | \tilde{k}_z = - \sqrt{ n^2 k^2_0 - |k_{\parallel}|^2 } | ||
</math> | </math> | ||
| − | + | and ''n'' is the complex [[refractive index]] of the substrate. The reflected intensity (which is what is measured experimentally) is <math>R_F = |r_f|^2</math>. Close to the critical angle (<math>\scriptstyle \theta_i \approx \theta_c</math>), the beam is strongly refracted and: | |
:<math> | :<math> | ||
| − | + | \tilde{k}_z = k \sqrt{ \theta_i - \theta_c } | |
| + | </math> | ||
| + | Thus, when the incident angle is less than the critical angle (<math>\scriptstyle \theta_i < \theta_c</math>), the transmitted wave-vector is purely imaginary: | ||
| + | \tilde{k}_z = i k \sqrt{ \theta_c - \theta_i } | ||
| + | This corresponds to the wave being totally externally reflected (evanescent probing only). Above the critical angle, the reflected intensity falls off rapidly: <math> R_F \sim \theta_i^{-4}</math> (c.f. [[Fresnel plot]]). | ||
| + | |||
| + | ===Rough interface=== | ||
| + | A flat interface with a small amount of roughness can be modelled using idealized uncorrelated roughness, which is characterized by a mean standard deviation of the height <math>\scriptstyle \sigma = \sqrt{ \left \langle h^2 \right \rangle }</math>: | ||
| + | :<math> | ||
| + | r_S = r_F e^{ -2 \sigma^2 k_z \tilde{k}_z } | ||
</math> | </math> | ||
For a substrate with a single continuous layer of thickness ''h'' (e.g. a uniform thin film), the reflectivity becomes: | For a substrate with a single continuous layer of thickness ''h'' (e.g. a uniform thin film), the reflectivity becomes: | ||
:<math> | :<math> | ||
| − | + | r_S = \frac{ r_{01} + r_{12} e^{ 2i \tilde{k}^1_z h } }{ 1 + r_{01} r_{12} e^{ 2i \tilde{k}^1_z h } } | |
</math> | </math> | ||
where | where | ||
| Line 36: | Line 46: | ||
Where <math>\scriptstyle r_{01}</math> and <math>\scriptstyle r_{12}</math> for the [[Material:Vacuum|vacuum]]-layer and layer-substrate interfaces, respectively. This is called the 'one-box model'. | Where <math>\scriptstyle r_{01}</math> and <math>\scriptstyle r_{12}</math> for the [[Material:Vacuum|vacuum]]-layer and layer-substrate interfaces, respectively. This is called the 'one-box model'. | ||
| − | ===Parratt formalism=== | + | ===Multiple interfaces: Parratt formalism=== |
| + | The reflectivity from a stack of different layers can be computed using the so-called Parratt recursion formalism, which accounts for the effect of reflection from each internal interface, including their coherent interference to yield the final reflection intensity. This formalism can, in fact, be used to simulate or fit an arbitrary electron-density distribution (in the film-normal direction). Any continuous variation of density can be simulated by discretizing the system into a finite number of layers of finite thickness. | ||
| + | |||
| + | The Parratt formalism is recursive | ||
| + | * L. G. Parratt [http://journals.aps.org/pr/abstract/10.1103/PhysRev.95.359 Surface Studies of Solids by Total Reflection of X-Rays] ''Phys. Rev.'' '''1954''', 95, 359. [http://dx.doi.org/10.1103/PhysRev.95.359 doi: 10.1103/PhysRev.95.359] | ||
| + | |||
| + | ===Master-Formula=== | ||
TBD | TBD | ||
| − | |||
==See Also== | ==See Also== | ||
Revision as of 16:05, 28 January 2015
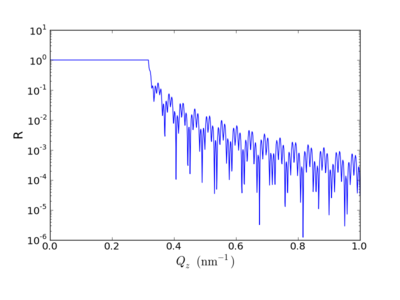
Reflectivity refers to the measurement of the intensity of reflection off of a flat interface. The term both describes the physical phenomenon, as well as the experimental technique.
X-ray Reflectivity (XRR or XR) and neutron reflectivity (NR) are techniques which measure the intensity of reflected radiation as a function of angle (where, by definition for specular reflectivity, the incident and exit angles are equal; ). A plot of reflectivity (R) versus angle yields the reflectivity curve. For XR and NR, the data is typically plotted as a function of the momentum transfer parallel to the film normal:
Contents
Off-Specular Reflectivity
TBD
Mathematical form
Ideal interface
In its simplest form, the Fresnel reflectivity can be given by:
Where is the vertical (z) component of the momentum of the incident wave, and is the vertical component of the transmitted wave:
and n is the complex refractive index of the substrate. The reflected intensity (which is what is measured experimentally) is . Close to the critical angle (), the beam is strongly refracted and:
Thus, when the incident angle is less than the critical angle (), the transmitted wave-vector is purely imaginary: \tilde{k}_z = i k \sqrt{ \theta_c - \theta_i } This corresponds to the wave being totally externally reflected (evanescent probing only). Above the critical angle, the reflected intensity falls off rapidly: (c.f. Fresnel plot).
Rough interface
A flat interface with a small amount of roughness can be modelled using idealized uncorrelated roughness, which is characterized by a mean standard deviation of the height :
For a substrate with a single continuous layer of thickness h (e.g. a uniform thin film), the reflectivity becomes:
where
is the perpendicular component of the wave-vector (in medium j). The reflectivity coefficients are:
Where and for the vacuum-layer and layer-substrate interfaces, respectively. This is called the 'one-box model'.
Multiple interfaces: Parratt formalism
The reflectivity from a stack of different layers can be computed using the so-called Parratt recursion formalism, which accounts for the effect of reflection from each internal interface, including their coherent interference to yield the final reflection intensity. This formalism can, in fact, be used to simulate or fit an arbitrary electron-density distribution (in the film-normal direction). Any continuous variation of density can be simulated by discretizing the system into a finite number of layers of finite thickness.
The Parratt formalism is recursive
- L. G. Parratt Surface Studies of Solids by Total Reflection of X-Rays Phys. Rev. 1954, 95, 359. doi: 10.1103/PhysRev.95.359
Master-Formula
TBD
See Also
- Fresnel plot
- Oscillations below the critical angle
- DWBA: A formalism for modeling GISAXS data, including reflection effects.