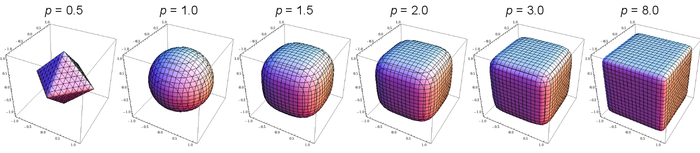
Form Factor:Superball

A superball is a general mathematical shape that can be used to describe rounded cubes. In fact, it is a general parametrization that can describe, via a parameter $p$:

• Empty space (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle p=0.0} )
• Concave octahedra ($p<0.5$)
• Octahedra ($p=0.5$)
• Convex octahedra ($0.5<p<1$)
• Spheres ($p=1$)
• Rounded cubes ($p>1$)
• Cubes ($p\to \infty$)

The general equation is parametrized by the size, $R$, and the curvature $p$:

${\begin{alignedat}{2}\left|{\frac {x}{R}}\right|^{2p}+\left|{\frac {y}{R}}\right|^{2p}+\left|{\frac {z}{R}}\right|^{2p}&\leq 1\\|x|^{2p}+|y|^{2p}+|z|^{2p}&\leq |R|^{2p}\\\end{alignedat}}$

Obviously for $p=1$, we recover the equation for a sphere. In the limit of large $p$, we obtain a cube.

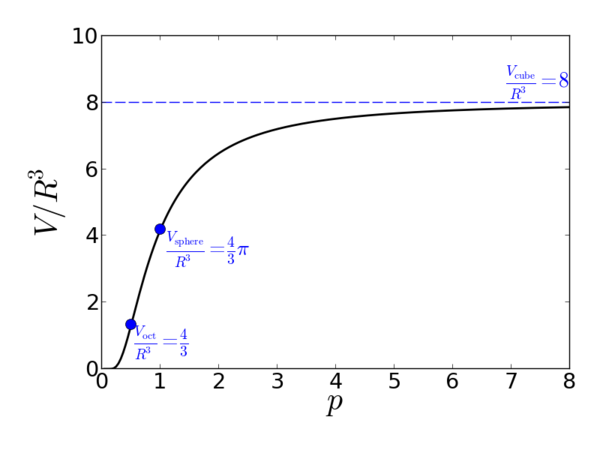
Volume

The normalized volume for a superball is:

${\frac {V_{\mathrm {sb} }}{R^{3}}}={\frac {2}{2p}}\mathrm {B} \left({\frac {1}{p}},{\frac {2p+1}{2p}}\right)\mathrm {B} \left({\frac {1}{2p}},{\frac {p+1}{p}}\right)$

Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{B}\left( x,y \right) = \Gamma(x)\Gamma(y)/\Gamma(x+y)} and $\Gamma (x)$ is the usual Euler gamma function.

Equations

The form factor for a superball is likely not analytic. However, it can be computed numerically.

References

Mathematical descriptions of superballs

• N. D. Elkies, A. M. Odlyzko and J. A. Rush "On the packing densities of superballs and other bodies" Inventiones Mathematicae Volume 105, Number 1 (1991), 613-639, doi: 10.1007/BF01232282
• Y. Jiao, F.H. Stillinger, S. Torquato "Optimal packings of superballs" Physical Review E 2009, 79, 041309, doi: 10.1103/PhysRevE.79.041309

Application to nanoscience

• Yugang Zhang, Fang Lu, Daniel van der Lelie, Oleg Gang "Continuous Phase Transformation in Nanocube Assemblies" Physical Review Letters 2011, 107, 135701 doi: 10.1103/PhysRevLett.107.135701