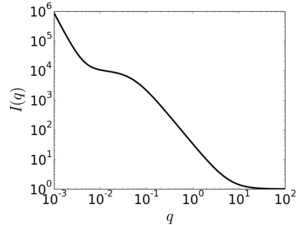
Example:Polymer clustering

Polymer solutions frequently exhibit some degree of clustering of the polymer chains. A more extreme case are hydrogels, where the polymer chains may be strongly-associated, or even crosslinked, into a network or mesh.

Hammouda et al. proposed the following functional form to describe scattering intensity from such systems:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I(q) = \frac{A}{q^n} + \frac{C}{1 + (q \xi)^m} + B }

where B is a constant background. The first term represents the Porod scattering from clusters, while the second term is a Lorentzian function ascribed to the scattering of the polymer chains themselves. In the context of a gel, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \xi} represents the average mesh size. The parameters A, C, n, and m may be used as fitting parameters.

Kratky plot

In a Kratky plot (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle q^2I(q) } vs. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle q} ), the equation becomes:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q^2 I(q) = \frac{A}{q^{n-2}} + \frac{C q^2}{1 + (q \xi)^m} + B q^2 }

See Also

• Diffuse scattering
• Boualem Hammouda, Derek L. Ho, and Steve Kline Insight into Clustering in Poly(ethylene oxide) Solutions Macromolecules 2004, 37 (18), 6932-6937. doi: 10.1021/ma049623d
• S.R. Kline "Reduction and Analysis of SANS and USANS Data using Igor Pro", J. Appl. Cryst. 2006, 39, 6, 895. doi:10.1107/S0021889806035059
• Takuro Matsunaga, Takamasa Sakai, Yuki Akagi, Ung-il Chung and Mitsuhiro Shibayama SANS and SLS Studies on Tetra-Arm PEG Gels in As-Prepared and Swollen States Macromolecules 2009, 42 (16), 6245–6252. doi: 10.1021/ma901013q
• R. A. Hule, R. P. Nagarkar, A. Altunbas, H. R. Ramay, M. C. Branco, J. P. Schneider and D. J. Pochan Correlations between structure, material properties and bioproperties in self-assembled β-hairpin peptide hydrogels Faraday Discuss. 2008, 139, 251–264. doi: 10.1039/B717616C
• R. A. Hule, R. P. Nagarkar, B. Hammouda, J. P. Schneider and D. J. Pochan Dependence of Self-Assembled Peptide Hydrogel Network Structure on Local Fibril Nanostructure Macromolecules 2009, 42, 7137–7145. doi: 10.1021/ma9003242
• B. Hammouda, F. Horkay and M. L. Becker Clustering and Solvation in Poly(acrylic acid) Polyelectrolyte Solutions Macromolecules 2005, 38, 2019–2021. doi: 10.1021/ma047960g
• Erika M. Saffer, Melissa A. Lackey, David M. Griffin, Suhasini Kishore, Gregory N. Tewb and Surita R. Bhatia SANS study of highly resilient poly(ethylene glycol) hydrogels Soft Matter 2014, 10,1905-1916. doi: 10.1039/C3SM52395K