Extra:Quantum wave time evolution example
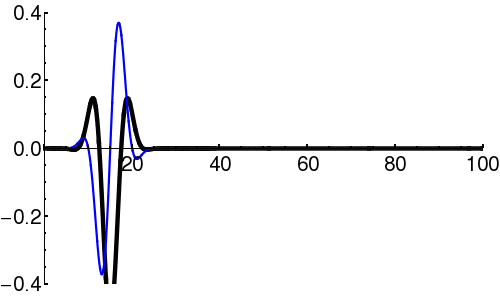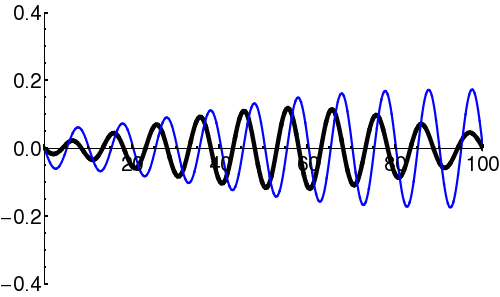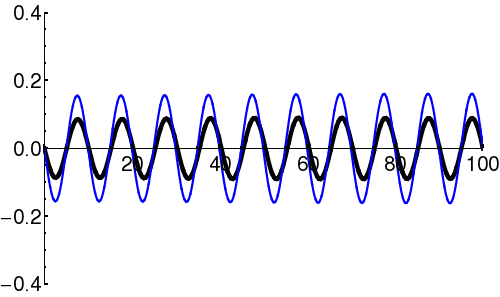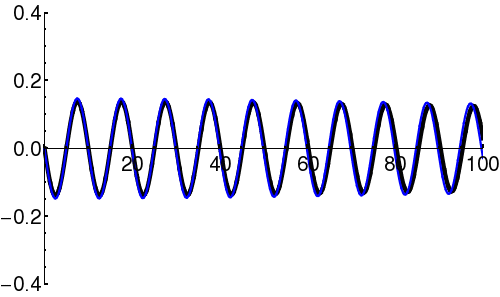
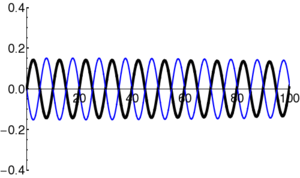
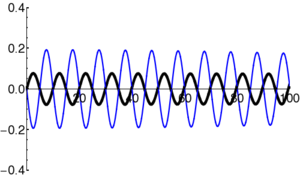
Particles in quantum mechanics can be thought of as wave packets that evolve in time according to the Schrödinger Equation. Even in cases where the square of the wavefunction () appears static ("stationary states"), the complex amplitude of the wavefunction () is in fact varying in time. In particular, the form of the time-dependent Schrödinger Equation demands that the amplitude oscillate (roughly, the amplitude oscillates between the real and imaginary components; i.e. the vector in the complex plane rotates continuously).
Example: Propagation and Interaction
Wave-packets can propagate, frequently with dispersion (which induces spatial spread of the envelope). Wave-packets can interact with barriers (defined by, e.g., some potential function), and interfere with themselves.
Example: Oscillation in Stationary State
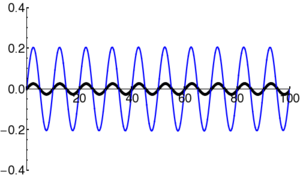
|
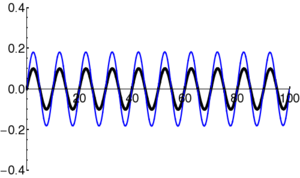
|

|
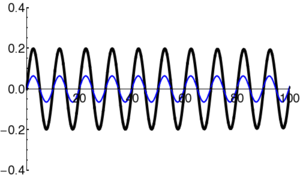
|

|
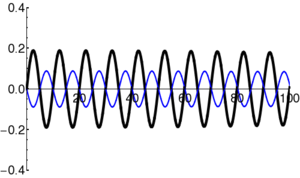
|
|
|