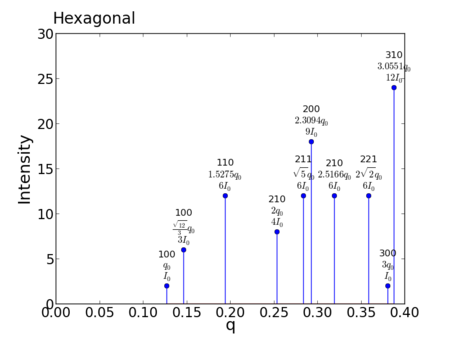
Lattice:Hexagonal
Hexagonal is a general class of lattice symmetries (i.e. how unit cells can be arranged in space).
Reciprocal-space Peaks
- Forbidden reflections, when both:
- odd
- Peak positions:
- For a = b = 1.0, c = 1.0:
peak q value h,k,l m f intensity intensity_scaled 1: 0.126933036509 1,0,0 2 1 2 0.192150 2: 0.146569645595 1,0,0 6 1 6 0.499222 3: 0.193893415997 1,1,0 12 1 12 0.754752 4: 0.253866073017 2,1,0 8 1 8 0.384301 5: 0.283830898224 2,1,1 12 1 12 0.515594 6: 0.293139291189 2,0,0 18 1 18 0.748832 7: 0.319441136669 2,1,0 12 1 12 0.458117 8: 0.359020843488 2,2,1 12 1 12 0.407613 9: 0.380799109526 3,0,0 2 1 2 0.064050 10: 0.387786831994 3,1,0 24 1 24 0.754752
Canonical 2D
A canonical 2D hexagonal lattice, such as formed by hexgonally-packed cylinders (where the c direction is conceptually infinite) has peak positions in the ratio: