The hexagonal diamond lattice is an arrangement of tetrahedrally-bonded elements, within a hexagonal unit cell. Whereas conventional diamond (a.k.a. cubic diamond) exists within a cubic unit cell, hexagonal diamond exists within a hexagonal unit cell. In both cases, elements are bonded tetrahdrally. However, in cubic diamond, the six-membered rings are all in the chair conformation, whereas in hexagonal diamond, some six-membered rings are in the boat conformation.
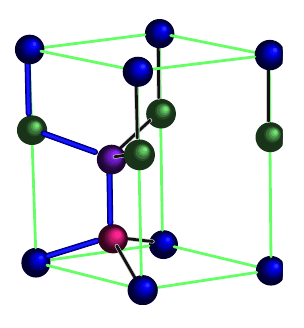
The four distinct positions in the unit cell are each given a different color. From: "Structural and vibrational properties of the 6H diamond: First-principles study"
doi: 10.1016/j.diamond.2006.03.013
Canonical Hexagonal Diamond
A canonical hexagonal diamond lattice (single atom/particle type arranged as shown above) has symmetry Fd3m.
Symmetry
- Crystal Family: Hexagonal
- Crystal System: Hexagonal
- Bravais Lattice: hexagonal
- Crystal class: Hexoctahedral
- Space Group: P63/mmc
- Particles per unit cell:

- Volume of unit cell:

- Dimensionality:

Structure
TBD
Particle Positions
There are 14 positions. In total there are 4 particles in the unit cell.
Fractional
Positions are given in terms of fractional coordinates relative to the unit-cell edge-vectors:











Absolute








Distances
For a particle-particle bond-length of  :
:





Absolute (in terms of particle-particle distance)








Examples
Atomics
- Lonsdaleite form of carbon (C), also known as hexagonal diamond, 2H diamond, or 'sp3 diamond' (a = 2.51 Å, c = 4.12 Å)
Alternating Hexagonal Diamond
This is the Wurtzite crystal structure, a hexagonal unit cell with alternating species.
Examples
Atomics
- Wurtzite (Zn,Fe)S (a = b = 3.82 Å, c = 6.26 Å)
Along Connections
This lattice can be thought of as the hexagonal-dimaond analog of the cubic-diamond cristobalite. Here, a four-bonded species occupies all the sites of the canonical hexagonal diamond lattice, and a two-bonded species sits along each of the connections between these tetrahedral sites.
Particle Positions
Particle Type A (bond tetrahedrally)
These are the same positions as the canonical hexagonal diamond.
Particle Type B (two-fold bonded)
There are 11 positions. In total there are 8 particles of this type in the unit cell.
Fractional
Positions are given in terms of fractional coordinates relative to the unit-cell edge-vectors:











See Also




































