Difference between revisions of "Lattice:Hexagonal"
KevinYager (talk | contribs) (Created page with "===Reciprocal-Space Peaks=== * Allowed reflections: * Peak positions: *: <math>q_{hkl}=2\pi\left( \frac{(h^2 + hk + k^2)^2}{a^2} + \frac{l^2}{c^2} \right)</math> *: For ''a'' ...") |
KevinYager (talk | contribs) |
||
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | ===Reciprocal- | + | '''Hexagonal''' is a general class of [[lattice]] symmetries (i.e. how [[unit cell]]s can be arranged in space). |
| − | * | + | |
| + | ===[[Reciprocal-space]] Peaks=== | ||
| + | * Forbidden reflections, when both: | ||
| + | ** <math>h + 2k = 3n</math> | ||
| + | ** <math>l</math> odd | ||
* Peak positions: | * Peak positions: | ||
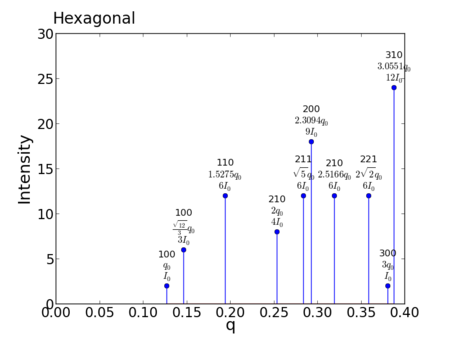
| − | *: <math>q_{hkl}=2\pi\left( \frac{(h^2 + hk + k^2)^ | + | *: <math>q_{hkl}=2\pi\left( \frac{(h^2 + hk + k^2)^?}{a^2} + \frac{l^2}{c^2} \right)^{1/2}</math> |
*: For ''a'' = ''b'' = 1.0, ''c'' = 1.0: | *: For ''a'' = ''b'' = 1.0, ''c'' = 1.0: | ||
<pre> | <pre> | ||
| Line 18: | Line 22: | ||
</pre> | </pre> | ||
[[Image:Lattice peaks-Hexagonal.png|450px]] | [[Image:Lattice peaks-Hexagonal.png|450px]] | ||
| + | |||
| + | ==Canonical 2D== | ||
| + | A canonical 2D hexagonal lattice, such as formed by hexgonally-packed cylinders (where the ''c'' direction is conceptually infinite) has peak positions in the ratio: | ||
| + | * <math>1:\sqrt{3}:2:\sqrt{7}:\sqrt{9}:\sqrt{12}:\sqrt{13}</math> | ||
| + | |||
| + | ==See Also== | ||
| + | * [[Lattice:HCP|Hexagonal close-packed (HCP)]] | ||
| + | * [[Lattice:Hexagonal diamond|Hexagonal diamond]] | ||
| + | ** [[Lattice:Wurtzite|Wurtzite]] | ||
| + | * [[Lattice:AlB2|AlB<sub>2</sub>]] | ||
Latest revision as of 08:23, 29 August 2019
Hexagonal is a general class of lattice symmetries (i.e. how unit cells can be arranged in space).
Reciprocal-space Peaks
- Forbidden reflections, when both:
- odd
- Peak positions:
- For a = b = 1.0, c = 1.0:
peak q value h,k,l m f intensity intensity_scaled 1: 0.126933036509 1,0,0 2 1 2 0.192150 2: 0.146569645595 1,0,0 6 1 6 0.499222 3: 0.193893415997 1,1,0 12 1 12 0.754752 4: 0.253866073017 2,1,0 8 1 8 0.384301 5: 0.283830898224 2,1,1 12 1 12 0.515594 6: 0.293139291189 2,0,0 18 1 18 0.748832 7: 0.319441136669 2,1,0 12 1 12 0.458117 8: 0.359020843488 2,2,1 12 1 12 0.407613 9: 0.380799109526 3,0,0 2 1 2 0.064050 10: 0.387786831994 3,1,0 24 1 24 0.754752
Canonical 2D
A canonical 2D hexagonal lattice, such as formed by hexgonally-packed cylinders (where the c direction is conceptually infinite) has peak positions in the ratio: