Difference between revisions of "Form Factor"
KevinYager (talk | contribs) |
KevinYager (talk | contribs) (→Specific form factors) |
||
| (37 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | ==Form | + | [[Image:Sphere form factor.png|thumb|right|300px|Example form factor scattering from a [[Form Factor:Sphere|sphere]].]] |
| + | |||
| + | The '''Form Factor''' ('''FF''') is the [[scattering]] which results from the ''shape'' of a particle. When particles are distributed without any particle-particle correlations (e.g. dilute solution of non-interacting particles, freely floating), then the scattering one observes is entirely the form factor. By comparison, when particles are in a well-defined structure, the scattering is dominated by the [[structure factor]]; though even in these cases the form factor continues to contribute, since it modulates both the structure factor and the [[diffuse scattering]]. | ||
| + | |||
| + | When reading discussions of scattering modeling, one must be careful about the usage of the term 'form factor'. This same term is often used to describe three different (though related) quantities: | ||
| + | * <math>F(\mathbf{q})</math>, the '''form factor amplitude''' arising from a single particle; this can be thought of as the 3D [[reciprocal-space]] of the particle, and is thus in general anisotropic. | ||
| + | * <math>|F(\mathbf{q})|^2</math>, the '''form factor intensity'''; whereas the amplitude cannot be measured experimentally, the form factor [[scattering intensity|intensity]] in principle can be. | ||
| + | * <math>P(q) = \left\langle |F(\mathbf{q})|^2 \right\rangle </math>, the '''isotropic form factor intensity'''; i.e. the orientational averaged of the form factor square. This is the 1D scattering that is measured for, e.g., particles freely distributed distributed in solution (since they tumble randomly and thus average over all possible orientations). | ||
| + | |||
| + | ==Equations== | ||
| + | In the most general case of an arbitrary distribution of [[Scattering Length Density|scattering density]], <math>\rho(\mathbf{r})</math>, the form factor is computed by integrating over all space: | ||
| + | |||
| + | :<math> | ||
| + | F_{j}(\mathbf{q}) = \int \rho_j(\mathbf{r}) e^{i \mathbf{q} \cdot \mathbf{r} } \mathrm{d}V | ||
| + | </math> | ||
| + | |||
| + | The subscript denotes that the form factor is for particle ''j''; in multi-component systems, each particle has its own form factor. For a particle of uniform density and volume ''V'', we denote the scattering contrast with respect to the ambient as <math>\Delta \rho</math>, and the form factor is simply: | ||
| + | |||
| + | :<math> | ||
| + | F_{j}(\mathbf{q}) = \Delta \rho \int\limits_{V} e^{i \mathbf{q} \cdot \mathbf{r} } \mathrm{d}V | ||
| + | </math> | ||
| + | |||
| + | For monodisperse particles, the average (isotropic) form factor intensity is an average over all possible particle orientations: | ||
| + | :<math> | ||
| + | \begin{alignat}{2} | ||
| + | P_j(q) & = \left\langle |F_j(\mathbf{q})|^2 \right\rangle \\ | ||
| + | & = \int\limits_{\phi=0}^{2\pi}\int\limits_{\theta=0}^{\pi} | F_j(-q\sin\theta\cos\phi,q\sin\theta\sin\phi,q\cos\theta)|^2 \sin\theta\mathrm{d}\theta\mathrm{d}\phi | ||
| + | \end{alignat} | ||
| + | </math> | ||
| + | |||
| + | Note that in cases where particles are not monodisperse, then the above average would also include averages over the distritubions in particle size and/or shape. Note that for <math>q=0</math>, we expect: | ||
| + | :<math> | ||
| + | \begin{alignat}{2} | ||
| + | F(0) & = \int\limits_{\mathrm{all\,\,space}} \rho(\mathbf{r}) e^{0} \mathrm{d}\mathbf{r} = \rho_{\mathrm{total}} \\ | ||
| + | & = \Delta \rho \int\limits_{V} e^{0} \mathrm{d}\mathbf{r} = \Delta \rho V | ||
| + | \end{alignat} | ||
| + | </math> | ||
| + | And so: | ||
| + | :<math> | ||
| + | \begin{alignat}{2} | ||
| + | P(0) & = \left\langle \left| F(0) \right|^2 \right\rangle \\ | ||
| + | & = 4 \pi \Delta \rho^2 V^2 | ||
| + | \end{alignat} | ||
| + | </math> | ||
| + | As expected, scattering intensity scales with the square of the scattering contrast and the particle volume. For multi-component systems, this has the effect of greatly emphasizing larger particles. For instance, a 2-fold increase in particle diameter results in a <math>(2^3)^2 = 64</math>-fold increase in scattering intensity. | ||
| + | |||
| + | ==Form Factor Equations== | ||
| + | * [[Atomic Form Factor]] | ||
* [[Form Factor:Sphere|Sphere]] | * [[Form Factor:Sphere|Sphere]] | ||
| + | * [[Form Factor:Ellipsoid of revolution|Ellipsoid of revolution]] | ||
* [[Form Factor:Cube|Cube]] | * [[Form Factor:Cube|Cube]] | ||
| + | * [[Form Factor:Octahedron|Octahedron]] | ||
| + | * [[Form Factor:Pyramid|Pyramid]] | ||
| + | * [[Form Factor:Superball|Superball]] (can be used to describe rounded cubes/octahedra/etc.) | ||
| + | |||
| + | ==Form Factor Equations in the Literature== | ||
| + | ===Reviews/summaries of form factors=== | ||
| + | The following is a partial list of form factors that have been published in the literature: | ||
| + | * [http://www.ncnr.nist.gov/resources/old_applets/index.html NCNR SANS solution form factors]: | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/Sphere.html Sphere] | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/PolyHardSphere.html PolyHardSphere] | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/PolyRectSphere.html PolyRectSphere] | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/CoreShell.html CoreShell] | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/PolyCoreShell.html PolyCoreShell] | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/PolyCoreShellRatio.html PolyCoreShellRatio] | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/Cylinder.html Cylinder] | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/HollowCylinder.html HollowCylinder] | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/CoreShellCylinder.html CoreShellCylinder] | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/Ellipsoid.html Ellipsoid] | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/OblateCoreShell.html OblateCoreShell] | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/ProlateCoreShell.html ProlateCoreShell] | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/TwoHomopolymerRPA.html TwoHomopolymerRPA] | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/DAB.html DAB] | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/TeubnerStrey.html TeubnerStrey] | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/Lorentz.html Lorentz] | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/PeakLorentz.html PeakLorentz] | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/PeakGauss.html PeakGauss] | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/PowerLaw.html PowerLaw] | ||
| + | ** [http://www.ncnr.nist.gov/resources/old_applets/sansmodels/BE_RPA.html BE_RPA] | ||
| + | |||
| + | * [http://ln-www.insp.upmc.fr/axe4/Oxydes/IsGISAXS/figures/doc/manual.html IsGISAXS, Born form factors] (see also Gilles Renaud, Rémi Lazzari,Frédéric Leroy "[http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6TVY-4X36TK4-1&_user=2422869&_coverDate=08%2F31%2F2009&_rdoc=1&_fmt=high&_orig=gateway&_origin=gateway&_sort=d&_docanchor=&view=c&_searchStrId=1702575836&_rerunOrigin=google&_acct=C000057228&_version=1&_urlVersion=0&_userid=2422869&md5=d5f357bfcbf9a39bb8e42cfeac555359&searchtype=a Probing surface and interface morphology with Grazing Incidence Small Angle X-Ray Scattering]" Surface Science Reports, 64 (8), 31 August 2009, 255-380 [http://dx.doi.org/10.1016/j.surfrep.2009.07.002 doi:10.1016/j.surfrep.2009.07.002]): | ||
| + | ** Parallelepiped | ||
| + | ** Pyramid | ||
| + | ** Cylinder | ||
| + | ** Cone | ||
| + | ** Prism 3 | ||
| + | ** Tetrahedron | ||
| + | ** Prism 6 | ||
| + | ** cone 6 | ||
| + | ** Sphere | ||
| + | ** Cubooctahedron | ||
| + | ** Facetted sphere | ||
| + | ** Full sphere | ||
| + | ** Full spheroid | ||
| + | ** Box | ||
| + | ** Anisotropic pyramid | ||
| + | ** Hemi-ellipsoid | ||
| + | |||
| + | * [http://apps.jcns.fz-juelich.de/src/BornAgain/FFCatalog.pdf BornAgain form factor catalog] (updated with each software release): Contains all form factors from IsGisaxs, plus the following: | ||
| + | ** hard particles: | ||
| + | *** Dodecahedron | ||
| + | *** Icosahedron | ||
| + | ** ripples: | ||
| + | *** sinusoidal (as in FitGisaxs) | ||
| + | *** saw-tooth (as in FitGisaxs) | ||
| + | ** soft particles (documentation forthcoming): | ||
| + | *** Gaussian ellipsoid | ||
| + | *** Ornstein-Zernike | ||
| + | |||
| + | * Pedersen Review: [http://linkinghub.elsevier.com/retrieve/pii/S0001868697003126 Analysis of small-angle scattering data from colloids and polymer solutions: modeling and least-squares fitting] Jan Skov Pedersen, Advances in Colloid and Interface Science 1997, 70, 171. [http://dx.doi.org/10.1016/S0001-8686(97)00312-6 doi: 10.1016/S0001-8686(97)00312-6] | ||
| + | *# Homogeneous sphere | ||
| + | *# Spherical shell | ||
| + | *# Spherical concentric shells | ||
| + | *# Particles consisting of spherical subunits | ||
| + | *# Ellipsoid of revolution | ||
| + | *# Tri-axial ellipsoid | ||
| + | *# Cube and rectangular parallelepipedons | ||
| + | *# Truncated octahedra | ||
| + | *# Faceted sphere | ||
| + | *# Cube with terraces | ||
| + | *# Cylinder | ||
| + | *# Cylinder with elliptical cross section | ||
| + | *# Cylinder with spherical end-caps | ||
| + | *# Infinitely thin rod | ||
| + | *# Infinitely thin circular disk | ||
| + | *# Fractal aggregates | ||
| + | *# Flexible polymers with Gaussian statistics | ||
| + | *# Flexible self-avoiding polymers | ||
| + | *# Semi-flexible polymers without self-avoidance | ||
| + | *# Semi-flexible polymers with self-avoidance | ||
| + | *# Star polymer with Gaussian statistics | ||
| + | *# Star-burst polymer with Gaussian statistics | ||
| + | *# Regular comb polymer with Gaussian statistics | ||
| + | *# Arbitrarily branched polymers with Gaussian statistics | ||
| + | *# Sphere with Gaussian chains attached | ||
| + | *# Ellipsoid with Gaussian chains attached | ||
| + | *# Cylinder with Gaussian chains attached | ||
| + | |||
| + | * [http://www.nature.com/nmat/journal/v9/n11/extref/nmat2870-s1.pdf Supplementary Information] of: Matthew R. Jones, Robert J. Macfarlane, Byeongdu Lee, Jian Zhang, Kaylie L. Young, Andrew J. Senesi, and Chad A. Mirkin "[http://www.nature.com/nmat/journal/v9/n11/full/nmat2870.html DNA-nanoparticle superlattices formed from anisotropic building blocks]" Nature Materials '''9''', 913-917, '''2010'''. [http://dx.doi.org/10.1038/nmat2870 doi: 10.1038/nmat2870] | ||
| + | *# Pyramid | ||
| + | *# Cube | ||
| + | *# Cylinder | ||
| + | *# Octahedron | ||
| + | *# Rhombic dodecahedron (RD) | ||
| + | *# Triangular prism | ||
| + | |||
| + | ===Form factors for classes of geometric shapes=== | ||
| + | * '''Platonic solids''': [http://scripts.iucr.org/cgi-bin/paper?S0021889811011691 Scattering functions of Platonic solids] Xin Li, Roger Pynn, Wei-Ren Chen, et al. ''Journal of Applied Crystallography'' '''2011''', 44, p.1 [http://dx.doi.org/10.1107/S0021889811011691 doi:10.1107/S0021889811011691] | ||
| + | *# Tetrahedron | ||
| + | *# Hexahedron (cube, parallelepiped, etc.) | ||
| + | *# Octahedron | ||
| + | *# Dodecahedron | ||
| + | *# Icosahedron | ||
| + | |||
| + | * '''Polyhedra''': | ||
| + | ** [http://scripts.iucr.org/cgi-bin/paper?aj5251 Scattering functions of polyhedra] A. Senesi and B. Lee ''J. Appl. Cryst.'' '''2015''', 48, 565-577. [http://dx.doi.org/10.1107/S1600576715002964 doi: 10.1107/S1600576715002964] | ||
| + | ** [http://scripts.iucr.org/cgi-bin/paper?fs5152 Form factor of any polyhedron: a general compact formula and its singularities] B. Croset ''Journal of Applied Crystallography'' '''2017'''. [https://doi.org/10.1107/S1600576717010147 doi: 10.1107/S1600576717010147] | ||
| + | ** [https://arxiv.org/abs/1703.00255 Form factor (Fourier shape transform) of polygon and polyhedron] J. Wuttke ''ArXiv'':1703.00255 | ||
| + | |||
| + | |||
| + | ===Specific form factors=== | ||
| + | * [http://www.eng.uc.edu/~gbeaucag/Classes/Analysis/Chapter8.html This tutorial] lists sphere, rod, disk, and Gaussian polymer coil. | ||
| + | * '''Block-Copolymer Micelles''': [http://pubs.acs.org/doi/abs/10.1021/ma9512115 Scattering Form Factor of Block Copolymer Micelles] Jan Skov Pedersen* and Michael C. Gerstenberg, Macromolecules, 1996, 29 (4), pp 1363–1365 [http://dx.doi.org/10.1021/ma9512115 DOI: 10.1021/ma9512115] | ||
| + | * '''Capped cylinder''': [http://scripts.iucr.org/cgi-bin/paper?S0021889804000020 Scattering from cylinders with globular end-caps]. H. Kaya. J. Appl. Cryst. (2004). 37, 223-230 [http://dx.doi.org/10.1107/S0021889804000020 doi: 10.1107/S0021889804000020] | ||
| + | * '''Lens-shaped disc'''" [http://scripts.iucr.org/cgi-bin/paper?aj5016 Scattering from capped cylinders. Addendum.] H. Kaya and N.-R. de Souza. J. Appl. Cryst. (2004). 37, 508-509 [http://dx.doi.org/10.1107/S0021889804005709 doi: 10.1107/S0021889804005709 ] | ||
| + | * '''Star polymer:''' | ||
| + | ** Benoit, H. [http://onlinelibrary.wiley.com/doi/10.1002/pol.1953.120110512/abstract On the effect of branching and polydispersity on the angular distribution of the light scattered by gaussian coils] ''J. Polym. Sci.'' '''1953''', 11, 507–510. [http://dx.doi.org/10.1002/pol.1953.120110512 doi: 10.1002/pol.1953.120110512] | ||
| + | ** Richter, D.; Farago, B.; Huang, J. S.; Fetters, L. J.; Ewen, B. [http://pubs.acs.org/doi/abs/10.1021/ma00191a085 A study of single-arm relaxation in a polystyrene star polymer by neutron spin echo spectroscopy] ''Macromoleules'' '''1989''', 22, 468–472. [http://dx.doi.org/10.1021/ma00191a085 doi: 10.1021/ma00191a085] | ||
| + | ** L. Willner, O. Jucknischke, D. Richter, J. Roovers, L.-L. Zhou, P. M. Toporowski, L. J. Fetters, J. S. Huang, M. Y. Lin, N. Hadjichristidis [http://pubs.acs.org/doi/abs/10.1021/ma00092a022 Structural Investigation of Star Polymers in Solution by Small-Angle Neutron Scattering] ''Macromolecules'' '''1994''', 27 (14), 3821–3829. [http://dx.doi.org/10.1021/ma00092a022 doi: 10.1021/ma00092a022] | ||
| + | ** Takuro Matsunaga, Takamasa Sakai, Yuki Akagi, Ung-il Chung and Mitsuhiro Shibayama [http://pubs.acs.org/doi/abs/10.1021/ma901013q SANS and SLS Studies on Tetra-Arm PEG Gels in As-Prepared and Swollen States] ''Macromolecules'' '''2009''', 42 (16), 6245–6252. [http://dx.doi.org/10.1021/ma901013q doi: 10.1021/ma901013q] | ||
| + | ** X. Li, C. Do, Y. Liu, L. Sánchez-Diáz, G. Smith and W.-R. Chen [http://scripts.iucr.org/cgi-bin/paper?fs5081 A scattering function of star polymers including excluded volume effects] ''J. Appl. Cryst.'' '''2014''', 47 [http://dx.doi.org/10.1107/S1600576714022249 doi: 10.1107/S1600576714022249] | ||
| + | ** Durgesh K. Rai, Gregory Beaucage, Kedar Ratkanthwar, Peter Beaucage, Ramnath Ramachandran, and Nikos Hadjichristidis [https://journals.aps.org/pre/abstract/10.1103/PhysRevE.92.012602 Determination of the interaction parameter and topological scaling features of symmetric star polymers in dilute solution] ''Phys. Rev. E'' '''2015''', 012602. [https://doi.org/10.1103/PhysRevE.92.012602 doi: 10.1103/PhysRevE.92.012602] | ||
| + | * '''Cylinders vs. ribbons in solution''': Y. Su, C. Burger, B. S. Hsiao and B. Chu [http://journals.iucr.org/j/issues/2014/02/00/fs5073/stdsup.html Characterization of TEMPO-oxidized cellulose nanofibers in aqueous suspension by small-angle X-ray scattering] ''J. Appl. Cryst. '''2014''', 47, 788. [http://dx.doi.org/10.1107/S1600576714005020 doi: 10.1107/S1600576714005020] | ||
| + | * '''Hollow cylinders''': Kun Lu , Jaby Jacob , Pappannan Thiyagarajan , Vincent P. Conticello , and David G. Lynn [http://pubs.acs.org/doi/full/10.1021/ja0341642 Exploiting Amyloid Fibril Lamination for Nanotube Self-Assembly] ''J. Am. Chem. Soc.'' '''2003''', 125 (21), 6391–6393. [http://dx.doi.org/10.1021/ja0341642 doi: 10.1021/ja0341642] | ||
| + | * '''Amino acids''': D. Tong, S. Yang and L. Lu [http://scripts.iucr.org/cgi-bin/paper?vg5046 Accurate optimization of amino acid form factors for computing small-angle X-ray scattering intensity of atomistic protein structures] ''J. Appl. Cryst.'' '''2016''', 49. [http://dx.doi.org/10.1107/S1600576716007962 doi: 10.1107/S1600576716007962] | ||
| + | * '''Helical nanostructures''': Max Burian and Heinz Amenitsch [http://journals.iucr.org/m/issues/2018/04/00/tj5016/index.html Dummy-atom modelling of stacked and helical nanostructures from solution scattering data] ''IUCrJ'' '''2018''' [https://doi.org/10.1107/S2052252518005493 DOI: 10.1107/S2052252518005493] | ||
| + | |||
| + | ==See Also== | ||
| + | * Computing the scattering for [[lattices of nano-objects]] also involves computing the form factor. | ||
| + | * M. Burian, G. Fritz-Popovski, M. He, M. V. Kovalenko, O. Paris and R. T. Lechner [http://scripts.iucr.org/cgi-bin/paper?vg5016 Considerations on the model-free shape retrieval of inorganic nanocrystals from small-angle scattering data] ''J. Appl. Cryst.'' '''2015''', 48, 857-868. [http://dx.doi.org/10.1107/S1600576715006846 10.1107/S1600576715006846] | ||
| + | * R. A. X. Persson and J. Bergenholtz [http://scripts.iucr.org/cgi-bin/paper?po5072 Efficient computation of the scattering intensity from systems of nonspherical particles] ''J. Appl. Cryst.'' '''2016''', 49 [http://dx.doi.org/10.1107/S1600576716011481 doi:10.1107/S1600576716011481] | ||
| + | * Bernard Croseta [http://scripts.iucr.org/cgi-bin/paper?fs5161 Form factor of rounded objects: the sections method] ''J. Appl. Cryst.'' '''2018''' [https://doi.org/10.1107/S1600576718007239 doi: 10.1107/S1600576718007239] | ||
Latest revision as of 10:45, 25 March 2022
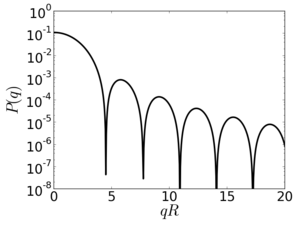
The Form Factor (FF) is the scattering which results from the shape of a particle. When particles are distributed without any particle-particle correlations (e.g. dilute solution of non-interacting particles, freely floating), then the scattering one observes is entirely the form factor. By comparison, when particles are in a well-defined structure, the scattering is dominated by the structure factor; though even in these cases the form factor continues to contribute, since it modulates both the structure factor and the diffuse scattering.
When reading discussions of scattering modeling, one must be careful about the usage of the term 'form factor'. This same term is often used to describe three different (though related) quantities:
- , the form factor amplitude arising from a single particle; this can be thought of as the 3D reciprocal-space of the particle, and is thus in general anisotropic.
- , the form factor intensity; whereas the amplitude cannot be measured experimentally, the form factor intensity in principle can be.
- , the isotropic form factor intensity; i.e. the orientational averaged of the form factor square. This is the 1D scattering that is measured for, e.g., particles freely distributed distributed in solution (since they tumble randomly and thus average over all possible orientations).
Contents
Equations
In the most general case of an arbitrary distribution of scattering density, , the form factor is computed by integrating over all space:
The subscript denotes that the form factor is for particle j; in multi-component systems, each particle has its own form factor. For a particle of uniform density and volume V, we denote the scattering contrast with respect to the ambient as , and the form factor is simply:
For monodisperse particles, the average (isotropic) form factor intensity is an average over all possible particle orientations:
Note that in cases where particles are not monodisperse, then the above average would also include averages over the distritubions in particle size and/or shape. Note that for , we expect:
And so:
As expected, scattering intensity scales with the square of the scattering contrast and the particle volume. For multi-component systems, this has the effect of greatly emphasizing larger particles. For instance, a 2-fold increase in particle diameter results in a -fold increase in scattering intensity.
Form Factor Equations
- Atomic Form Factor
- Sphere
- Ellipsoid of revolution
- Cube
- Octahedron
- Pyramid
- Superball (can be used to describe rounded cubes/octahedra/etc.)
Form Factor Equations in the Literature
Reviews/summaries of form factors
The following is a partial list of form factors that have been published in the literature:
- IsGISAXS, Born form factors (see also Gilles Renaud, Rémi Lazzari,Frédéric Leroy "Probing surface and interface morphology with Grazing Incidence Small Angle X-Ray Scattering" Surface Science Reports, 64 (8), 31 August 2009, 255-380 doi:10.1016/j.surfrep.2009.07.002):
- Parallelepiped
- Pyramid
- Cylinder
- Cone
- Prism 3
- Tetrahedron
- Prism 6
- cone 6
- Sphere
- Cubooctahedron
- Facetted sphere
- Full sphere
- Full spheroid
- Box
- Anisotropic pyramid
- Hemi-ellipsoid
- BornAgain form factor catalog (updated with each software release): Contains all form factors from IsGisaxs, plus the following:
- hard particles:
- Dodecahedron
- Icosahedron
- ripples:
- sinusoidal (as in FitGisaxs)
- saw-tooth (as in FitGisaxs)
- soft particles (documentation forthcoming):
- Gaussian ellipsoid
- Ornstein-Zernike
- hard particles:
- Pedersen Review: Analysis of small-angle scattering data from colloids and polymer solutions: modeling and least-squares fitting Jan Skov Pedersen, Advances in Colloid and Interface Science 1997, 70, 171. doi: 10.1016/S0001-8686(97)00312-6
- Homogeneous sphere
- Spherical shell
- Spherical concentric shells
- Particles consisting of spherical subunits
- Ellipsoid of revolution
- Tri-axial ellipsoid
- Cube and rectangular parallelepipedons
- Truncated octahedra
- Faceted sphere
- Cube with terraces
- Cylinder
- Cylinder with elliptical cross section
- Cylinder with spherical end-caps
- Infinitely thin rod
- Infinitely thin circular disk
- Fractal aggregates
- Flexible polymers with Gaussian statistics
- Flexible self-avoiding polymers
- Semi-flexible polymers without self-avoidance
- Semi-flexible polymers with self-avoidance
- Star polymer with Gaussian statistics
- Star-burst polymer with Gaussian statistics
- Regular comb polymer with Gaussian statistics
- Arbitrarily branched polymers with Gaussian statistics
- Sphere with Gaussian chains attached
- Ellipsoid with Gaussian chains attached
- Cylinder with Gaussian chains attached
- Supplementary Information of: Matthew R. Jones, Robert J. Macfarlane, Byeongdu Lee, Jian Zhang, Kaylie L. Young, Andrew J. Senesi, and Chad A. Mirkin "DNA-nanoparticle superlattices formed from anisotropic building blocks" Nature Materials 9, 913-917, 2010. doi: 10.1038/nmat2870
- Pyramid
- Cube
- Cylinder
- Octahedron
- Rhombic dodecahedron (RD)
- Triangular prism
Form factors for classes of geometric shapes
- Platonic solids: Scattering functions of Platonic solids Xin Li, Roger Pynn, Wei-Ren Chen, et al. Journal of Applied Crystallography 2011, 44, p.1 doi:10.1107/S0021889811011691
- Tetrahedron
- Hexahedron (cube, parallelepiped, etc.)
- Octahedron
- Dodecahedron
- Icosahedron
- Polyhedra:
- Scattering functions of polyhedra A. Senesi and B. Lee J. Appl. Cryst. 2015, 48, 565-577. doi: 10.1107/S1600576715002964
- Form factor of any polyhedron: a general compact formula and its singularities B. Croset Journal of Applied Crystallography 2017. doi: 10.1107/S1600576717010147
- Form factor (Fourier shape transform) of polygon and polyhedron J. Wuttke ArXiv:1703.00255
Specific form factors
- This tutorial lists sphere, rod, disk, and Gaussian polymer coil.
- Block-Copolymer Micelles: Scattering Form Factor of Block Copolymer Micelles Jan Skov Pedersen* and Michael C. Gerstenberg, Macromolecules, 1996, 29 (4), pp 1363–1365 DOI: 10.1021/ma9512115
- Capped cylinder: Scattering from cylinders with globular end-caps. H. Kaya. J. Appl. Cryst. (2004). 37, 223-230 doi: 10.1107/S0021889804000020
- Lens-shaped disc" Scattering from capped cylinders. Addendum. H. Kaya and N.-R. de Souza. J. Appl. Cryst. (2004). 37, 508-509 doi: 10.1107/S0021889804005709
- Star polymer:
- Benoit, H. On the effect of branching and polydispersity on the angular distribution of the light scattered by gaussian coils J. Polym. Sci. 1953, 11, 507–510. doi: 10.1002/pol.1953.120110512
- Richter, D.; Farago, B.; Huang, J. S.; Fetters, L. J.; Ewen, B. A study of single-arm relaxation in a polystyrene star polymer by neutron spin echo spectroscopy Macromoleules 1989, 22, 468–472. doi: 10.1021/ma00191a085
- L. Willner, O. Jucknischke, D. Richter, J. Roovers, L.-L. Zhou, P. M. Toporowski, L. J. Fetters, J. S. Huang, M. Y. Lin, N. Hadjichristidis Structural Investigation of Star Polymers in Solution by Small-Angle Neutron Scattering Macromolecules 1994, 27 (14), 3821–3829. doi: 10.1021/ma00092a022
- Takuro Matsunaga, Takamasa Sakai, Yuki Akagi, Ung-il Chung and Mitsuhiro Shibayama SANS and SLS Studies on Tetra-Arm PEG Gels in As-Prepared and Swollen States Macromolecules 2009, 42 (16), 6245–6252. doi: 10.1021/ma901013q
- X. Li, C. Do, Y. Liu, L. Sánchez-Diáz, G. Smith and W.-R. Chen A scattering function of star polymers including excluded volume effects J. Appl. Cryst. 2014, 47 doi: 10.1107/S1600576714022249
- Durgesh K. Rai, Gregory Beaucage, Kedar Ratkanthwar, Peter Beaucage, Ramnath Ramachandran, and Nikos Hadjichristidis Determination of the interaction parameter and topological scaling features of symmetric star polymers in dilute solution Phys. Rev. E 2015, 012602. doi: 10.1103/PhysRevE.92.012602
- Cylinders vs. ribbons in solution: Y. Su, C. Burger, B. S. Hsiao and B. Chu Characterization of TEMPO-oxidized cellulose nanofibers in aqueous suspension by small-angle X-ray scattering J. Appl. Cryst. 2014, 47, 788. doi: 10.1107/S1600576714005020
- Hollow cylinders: Kun Lu , Jaby Jacob , Pappannan Thiyagarajan , Vincent P. Conticello , and David G. Lynn Exploiting Amyloid Fibril Lamination for Nanotube Self-Assembly J. Am. Chem. Soc. 2003, 125 (21), 6391–6393. doi: 10.1021/ja0341642
- Amino acids: D. Tong, S. Yang and L. Lu Accurate optimization of amino acid form factors for computing small-angle X-ray scattering intensity of atomistic protein structures J. Appl. Cryst. 2016, 49. doi: 10.1107/S1600576716007962
- Helical nanostructures: Max Burian and Heinz Amenitsch Dummy-atom modelling of stacked and helical nanostructures from solution scattering data IUCrJ 2018 DOI: 10.1107/S2052252518005493
See Also
- Computing the scattering for lattices of nano-objects also involves computing the form factor.
- M. Burian, G. Fritz-Popovski, M. He, M. V. Kovalenko, O. Paris and R. T. Lechner Considerations on the model-free shape retrieval of inorganic nanocrystals from small-angle scattering data J. Appl. Cryst. 2015, 48, 857-868. 10.1107/S1600576715006846
- R. A. X. Persson and J. Bergenholtz Efficient computation of the scattering intensity from systems of nonspherical particles J. Appl. Cryst. 2016, 49 doi:10.1107/S1600576716011481
- Bernard Croseta Form factor of rounded objects: the sections method J. Appl. Cryst. 2018 doi: 10.1107/S1600576718007239











