Difference between revisions of "Scattering"
KevinYager (talk | contribs) (→See Also) |
|||
| (18 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
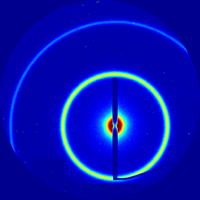
| − | '''Scattering''' broadly refers to experimental techniques that use the interaction between radiation and matter to elucidate structure. In [[x-ray]] scattering, a collimated x-ray beam is directed at a sample of interest. The incident x-rays scatter off of all the atoms/particles in the sample. Because of the wavelike nature of x-rays (which are simply high-energy photons; i.e. electromagnetic rays), the scattered waves interfere with one another, leading to constructive interference at some angles, but destructive interference at other angles. The | + | [[Image:Standard-AgBH-gisaxs th000 spot3 60sec SAXS.png|thumb|200px|right|Example scattering pattern (for [[Material:Silver behenate|AgBH]]). The [[Scattering_features#Rings|rings]] of scattering at well-defined angles arise from scattering off of the lamellar order in the sample.]] |
| + | |||
| + | '''Scattering''' broadly refers to experimental techniques that use the interaction between radiation and matter to elucidate structure. In [[x-ray]] scattering, a collimated x-ray beam is directed at a sample of interest. The incident x-rays scatter off of all the atoms/particles in the sample. Because of the wavelike nature of x-rays (which are simply high-[[X-ray energy|energy]] photons; i.e. electromagnetic rays), the scattered waves interfere with one another, leading to constructive interference at some angles, but destructive interference at other angles. The end result is a [[Scattering features|pattern]] of scattered [[Scattering intensity|radiation]] (as a function of angle with respect to the direct beam) that encodes the microscopic, nanoscopic, and molecular-scale structure of the sample. | ||
==Geometry== | ==Geometry== | ||
| Line 14: | Line 16: | ||
:<math> | :<math> | ||
\begin{alignat}{2} | \begin{alignat}{2} | ||
| − | q = |\mathbf{q}| & = k \sin { \ | + | q = |\mathbf{q}| & = 2 k \sin { ( 2 \theta_s /2 ) } \\ |
| − | + | & = \frac{4 \pi}{\lambda} \sin{ \theta_s } | |
| − | & = \frac{4 \pi}{\lambda} \sin{ \ | ||
\end{alignat} | \end{alignat} | ||
</math> | </math> | ||
| + | Where <math>\scriptstyle 2 \theta_s </math> is the scattering angle. | ||
| + | |||
| + | See also [[Geometry:TSAXS 3D]]. | ||
==Theory== | ==Theory== | ||
| − | The mathematical form of scattering is closely related to the [[Fourier transform]]. The sample's realspace density distribution is Fourier transformed into an abstract 3D [[reciprocal-space]]; scattering probes this inverse space. | + | The mathematical form of scattering is closely related to the [[Fourier transform]]. The sample's [[realspace]] density distribution is Fourier transformed into an abstract 3D [[reciprocal-space]]; scattering probes this inverse space. The fundamental equation in scattering is: |
| + | :<math> | ||
| + | \begin{alignat}{2} | ||
| + | I(\mathbf{q}) | ||
| + | & = \left\langle \left| \sum_{n=1}^{N} \rho_{n} e^{i \mathbf{q} \cdot \mathbf{r}_n } \right|^2 \right\rangle \\ | ||
| + | \end{alignat} | ||
| + | </math> | ||
| + | Where the observed [[scattering intensity]] (''I'') in the 3D reciprocal-space ('''q''') is given by an ensemble average of the intensity for all (''N'') scattering entities probed by the beam. The wave-matter interaction is given by inner term, which coherently sums (interferes) the complex scattering contributions (<math>\rho_n</math> denotes the scattering power) of the ''N'' entities; the exponential term represents a plane wave (incident radiation). In integral form (for a continuous function of the scattering density <math>\rho(\mathbf{r})</math>), we can write an integral over all of real-space: | ||
| + | :<math> | ||
| + | \begin{alignat}{2} | ||
| + | I(\mathbf{q}) | ||
| + | & = \left| \int\limits_{V} \rho(\mathbf{r}) e^{i \mathbf{q} \cdot \mathbf{r} } \mathrm{d}V \right|^2 \\ | ||
| + | \end{alignat} | ||
| + | </math> | ||
| + | The inner component can be thought of as the [[reciprocal-space]]: | ||
| + | :<math> | ||
| + | \begin{alignat}{2} | ||
| + | |||
| + | F(\mathbf{q}) & = \int\limits \rho(\mathbf{r}) e^{i \mathbf{q} \cdot \mathbf{r} } \mathrm{d}V \\ | ||
| + | |||
| + | \end{alignat} | ||
| + | </math> | ||
| + | This is mathematically identical to the (three-dimensional) [[Fourier transform]]. | ||
| + | |||
| + | |||
| + | ==See Also== | ||
| + | * [[Bragg's law]] | ||
| + | * [[Diffraction]] | ||
| + | * [[Fourier transform]] | ||
| + | * Geometry: | ||
| + | ** [[Geometry:TSAXS 3D|TSAXS 3D]] | ||
| + | ** [[Geometry:WAXS 3D|WSAXS 3D]] | ||
Latest revision as of 09:29, 23 January 2018
Scattering broadly refers to experimental techniques that use the interaction between radiation and matter to elucidate structure. In x-ray scattering, a collimated x-ray beam is directed at a sample of interest. The incident x-rays scatter off of all the atoms/particles in the sample. Because of the wavelike nature of x-rays (which are simply high-energy photons; i.e. electromagnetic rays), the scattered waves interfere with one another, leading to constructive interference at some angles, but destructive interference at other angles. The end result is a pattern of scattered radiation (as a function of angle with respect to the direct beam) that encodes the microscopic, nanoscopic, and molecular-scale structure of the sample.
Geometry
We define a vector in reciprocal-space as the difference between the incident and scattered x-ray beams. This new vector is the momentum transfer, denoted by q:
The length of this vector is:
Where is the scattering angle.
See also Geometry:TSAXS 3D.
Theory
The mathematical form of scattering is closely related to the Fourier transform. The sample's realspace density distribution is Fourier transformed into an abstract 3D reciprocal-space; scattering probes this inverse space. The fundamental equation in scattering is:
Where the observed scattering intensity (I) in the 3D reciprocal-space (q) is given by an ensemble average of the intensity for all (N) scattering entities probed by the beam. The wave-matter interaction is given by inner term, which coherently sums (interferes) the complex scattering contributions ( denotes the scattering power) of the N entities; the exponential term represents a plane wave (incident radiation). In integral form (for a continuous function of the scattering density ), we can write an integral over all of real-space:
The inner component can be thought of as the reciprocal-space:
This is mathematically identical to the (three-dimensional) Fourier transform.
See Also
- Bragg's law
- Diffraction
- Fourier transform
- Geometry: