Lattice:Hexagonal diamond

The hexagonal diamond lattice is an arrangement of tetrahedrally-bonded elements, within a hexagonal unit cell. Whereas conventional diamond (a.k.a. cubic diamond) exists within a cubic unit cell, hexagonal diamond exists within a hexagonal unit cell. In both cases, elements are bonded tetrahdrally. However, in cubic diamond, the six-membered rings are all in the chair conformation, whereas in hexagonal diamond, some six-membered rings are in the boat conformation.

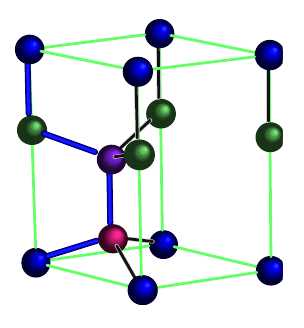
The four distinct positions in the unit cell are each given a different color. From: "Structural and vibrational properties of the 6H diamond: First-principles study" doi: 10.1016/j.diamond.2006.03.013

Canonical Hexagonal Diamond

A canonical hexagonal diamond lattice (single atom/particle type arranged as shown above) has symmetry Fd3m.

Symmetry

• Crystal Family: Hexagonal
• Crystal System: Hexagonal
• Bravais Lattice: hexagonal
• Crystal class: Hexoctahedral
• Space Group: P6₃/mmc
• Particles per unit cell: $n=4$
• Volume of unit cell: $V_{d}=a^{2}c\sin(60^{\circ })=a^{2}c{\frac {\sqrt {3}}{2}}$
• Dimensionality: $d=3$

Structure

TBD

Particle Positions

There are 14 positions. In total there are 4 particles in the unit cell.

Fractional

Positions are given in terms of fractional coordinates relative to the unit-cell edge-vectors:

$\mathbf {a} =(a,0,0)$

$\mathbf {b} =(b/2,{\sqrt {3}}b/2,0)$

$\mathbf {c} =(0,0,c)$

• $4\,\mathrm {bottom\,\,layer} :\,{\frac {1}{12}}+{\frac {1}{6}}+{\frac {1}{12}}+{\frac {1}{6}}={\frac {1}{2}}$
  • $\left(0,0,0\right),(1,0,0),(0,1,0),(1,1,0)$
• $4\,\mathrm {mid\,\,layer} :\,{\frac {1}{6}}+{\frac {1}{3}}+{\frac {1}{6}}+{\frac {1}{3}}=1$
  • $\left(0,0,{\frac {5}{8}}\right),\left(1,0,{\frac {5}{8}}\right),\left(0,1,{\frac {5}{8}}\right),\left(1,1,{\frac {5}{8}}\right)$
• $2\,\mathrm {internal\,\,strut} :\,1+1=2$
  • $\left({\frac {1}{3}},{\frac {1}{3}},{\frac {1}{8}}\right),\left({\frac {1}{3}},{\frac {1}{3}},{\frac {4}{8}}\right)$
• $4\,\mathrm {top\,\,layer} :\,{\frac {1}{12}}+{\frac {1}{6}}+{\frac {1}{12}}+{\frac {1}{6}}={\frac {1}{2}}$
  • $\left(0,0,1\right),(1,0,1),(0,1,1),(1,1,1)$

Absolute

• $4\,\mathrm {bottom\,\,layer} :\,{\frac {1}{12}}+{\frac {1}{6}}+{\frac {1}{12}}+{\frac {1}{6}}={\frac {1}{2}}$
  • $\left(0,0,0\right),(a,0,0),\left({\frac {b}{2}},{\frac {{\sqrt {3}}b}{2}},0\right),\left(a+{\frac {b}{2}},{\frac {{\sqrt {3}}b}{2}},0\right)$
• $4\,\mathrm {mid\,\,layer} :\,{\frac {1}{6}}+{\frac {1}{3}}+{\frac {1}{6}}+{\frac {1}{3}}=1$
  • $\left(0,0,{\frac {5c}{8}}\right),\left(a,0,{\frac {5c}{8}}\right),\left({\frac {b}{2}},{\frac {{\sqrt {3}}b}{2}},{\frac {5c}{8}}\right),\left(a+{\frac {b}{2}},{\frac {{\sqrt {3}}b}{2}},{\frac {5c}{8}}\right)$
• $2\,\mathrm {internal\,\,strut} :\,1+1=2$
  • $\left({\frac {a}{2}},{\frac {b}{2{\sqrt {3}}}},{\frac {c}{8}}\right),\left({\frac {a}{2}},{\frac {b}{2{\sqrt {3}}}},{\frac {4c}{8}}\right)$
• $4\,\mathrm {top\,\,layer} :\,{\frac {1}{12}}+{\frac {1}{6}}+{\frac {1}{12}}+{\frac {1}{6}}={\frac {1}{2}}$
  • $\left(0,0,c\right),(a,0,c),\left({\frac {b}{2}},{\frac {{\sqrt {3}}b}{2}},c\right),\left(a+{\frac {b}{2}},{\frac {{\sqrt {3}}b}{2}},c\right)$

Distances

For a particle-particle bond-length of $l$:

$a={\frac {2{\sqrt {6}}}{3}}l$

$c={\frac {8}{3}}l$

${\frac {a}{c}}={\frac {\sqrt {6}}{4}}\approx 0.61237$

${\frac {c}{a}}={\frac {4}{\sqrt {6}}}\approx 1.63299$

Examples

Atomics

• Lonsdaleite form of carbon (C), also known as hexagonal diamond, 2H diamond, or 'sp³ diamond' (a = 2.51 Å, c = 4.12 Å)

Alternating Hexagonal Diamond

This is the Wurtzite crystal structure, a hexgonal unit cell with alternating species.

Examples

Atomics

• Wurtzite (Zn,Fe)S (a = b = 3.82 Å, c = 6.26 Å)

Along Connections

This lattice can be thought of as the hexagonal-dimaond analog of the cubic-diamond cristobalite. Here, a four-bonded species occupies all the sites of the canonical hexagonal diamond lattice, and a two-bonded species sits along each of the connections between these tetrahedral sites.

Particle Positions

Particle Type A (bond tetrahedrally)

These are the same positions as the canonical hexagonal diamond.

Particle Type B (two-fold bonded)

There are 11 positions. In total there are 8 particles of this type in the unit cell.

Fractional

Positions are given in terms of fractional coordinates relative to the unit-cell edge-vectors:

$\mathbf {a} =(a,0,0)$

$\mathbf {b} =(b/2,{\sqrt {3}}b/2,0)$

$\mathbf {c} =(0,0,c)$

• $3\,\mathrm {lower\,\,tripod} :\,1+1+1=3$
  • $\left({\frac {1}{6}},{\frac {1}{6}},{\frac {1}{16}}\right),\left({\frac {4}{6}},{\frac {1}{6}},{\frac {1}{16}}\right),\left({\frac {1}{6}},{\frac {4}{6}},{\frac {1}{16}}\right)$
• $1\,\mathrm {mid\,\,strut} :\,1=1$
  • $\left({\frac {1}{3}},{\frac {1}{3}},{\frac {5}{16}}\right)$
• $3\,\mathrm {midlevel\,\,tripod} :\,1+1+1=3$
  • $\left({\frac {1}{6}},{\frac {1}{6}},{\frac {9}{16}}\right),\left({\frac {4}{6}},{\frac {1}{6}},{\frac {9}{16}}\right),\left({\frac {1}{6}},{\frac {4}{6}},{\frac {9}{16}}\right)$
• $4\,\mathrm {upper\,\,connections} :\,{\frac {1}{6}}+{\frac {1}{3}}+{\frac {1}{6}}+{\frac {1}{3}}=1$
  • $\left(0,0,{\frac {13}{16}}\right),\left(1,0,{\frac {13}{16}}\right),\left(0,1,{\frac {13}{16}}\right),\left(1,1,{\frac {13}{16}}\right)$

See Also

• Lonsdaleite (Wikipedia)
• Cubic Diamond Lattice