Lattices of nano-objects

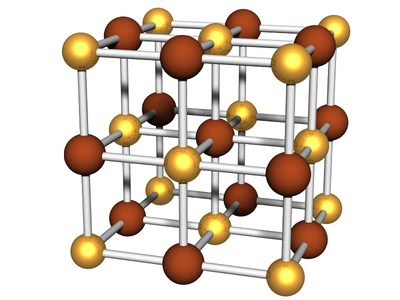
Lattices of nanoscale objects are now commonly being generated. Their scattering can be thought of as analogous to atomic crystals. In regular crystals, the atoms form a well-defined unit cell that repeats throughout space to form a lattice. This gives rise to well-defined peaks in reciprocal space. Superlattices can be thought of as the nanoscale analogue: the distance-scales are larger, but again we have objects packing into well-defined symmetry that repeats throughout space. To a first approximation, SAXS data from these systems can thus be interpreted by comparing the peak positions to the known peak patterns for various crystallographic symmetries.

However, quantitative analysis requires more care, since nano-object assembly can be quite different from atomic assembly:

1. The constituent objects are not atoms (simple point-like scattering objects with generally spherical symmetry). Nanoparticles can have unique shapes, can exhibit polydispersity, etc.
2. The kinds of disorder that arise in nanoscale systems may be quite different from atomic systems. For example, all atoms are exactly identical, whereas nano-objects exhibit polydispersity in size, shape, orientation, composition, etc. Furthermore, the lattice itself is formed through 'softer' interactions, and may be more disordered than atomic systems (and more tolerant to, e.g., vacancy or substitutional defects).
3. The symmetries that form from nano-objects may have no atomic examples. Atomic packing is generally extremely 'tight'; the atoms are volume filling and exhibit directional bonding dictated by the local symmetry of bonding orbitals. In nano-systems, very different kinds of interactions may be exploited. Some systems may be simple close-packed; whereas others may be comparatively open and sparse.
4. There are many nanoscale systems which can be thought of, conceptually, as nano-objects sitting on a lattice, but which are formed in a very different way. For instance, block-copolymers can be modelled as nano-objects on a lattice, but their elementary constituents are in fact the polymer chains (whose individual shape does not readily appear in the scattering signal).

Specific models

A variety of models have been presented to account for specific kinds of arrangements of nano-objects:

• Particles on a lattice: Scattering Curves of Ordered Mesoscopic Materials S. Förster, A. Timmann, M. Konrad, C. Schellbach, A. Meyer, S.S. Funari, P. Mulvaney, R. Knott, J. Phys. Chem. B, 2005, 109 (4), pp 1347–1360 DOI: 10.1021/jp0467494
• Lamellae: SAXS of self-assembled oriented lamellar nanocomposite films: an advanced method of evaluation W. Ruland and B. Smarsly J. Appl. Cryst. (2004). 37, 575-584 doi:10.1107/S0021889804011288
• Cylinders: SAXS of self-assembled nanocomposite films with oriented two-dimensional cylinder arrays: an advanced method of evaluation W. Ruland and B. Smarsly J. Appl. Cryst. (2005). 38, 78-86 doi:10.1107/S0021889804027724
• Spheres: Two-dimensional small-angle X-ray scattering of self-assembled nanocomposite films with oriented arrays of spheres: determination of lattice type, preferred orientation, deformation and imperfection W. Ruland and B. M. Smarsly J. Appl. Cryst. (2007). 40, 409-417 doi:10.1107/S0021889807010503
• Disordered 2D array of spheres: Scattering of electromagnetic waves by a disordered two-dimensional array of spheres N. Stefanou, A. Modinos. J. Phys.: Condens. Matter 1993, 5, 8859.

General models

Multicomponent lattice of nano-objects model

• Yager, K.G.; Zhang, Y.; Lu, F.; Gang, O. "Periodic lattices of arbitrary nano-objects: modeling and applications for self-assembled systems" Journal of Applied Crystallography 2014, 47, 118–129. doi: 10.1107/S160057671302832X

This paper describes a general model for simulating (and fitting) small-angle scattering data for periodic lattices of nanoparticles. The model is general, allowing for anisotropic nanoparticles (cubes, octahedra, etc.) with prescribed orientations within the lattice. The lattice may also contain a variety of different particles (with different sizes, shapes, or compositions). The model also accounts for various kinds of disorder relevant to nanoscale systems: finite grain size, polydispersity in particle properties (size, shape, orientation), lattice defects (e.g. vacancies), and so on.

See Also

• Discussion of scattering from multiple distinct components in unit cell; see Supplementary Information of: Petr Cigler, Abigail K. R. Lytton-Jean, Daniel G. Anderson, M. G. and Sung Yong Park DNA-controlled assembly of a NaTl lattice structure from gold nanoparticles and protein nanoparticles Nature Materials 2010, 9, 918-922 doi:10.1038/nmat2877
• Presentation of a essential equations for modeling a lattice with anisotropic nano-objects; see Supplementary Information of: Matthew R. Jones, Robert J. Macfarlane, Byeongdu Lee, Jian Zhang, Kaylie L. Young, Andrew J. Senesi, and Chad A. Mirkin DNA-nanoparticle superlattices formed from anisotropic building blocks Nature Materials 2010, 9, 913-917 doi: 10.1038/nmat2870 See also summary of mathematics.