Lattice:Diamond

The diamond lattice, which consists of tetrahedrally-arranged atoms/particles, has simple cubic symmetry.

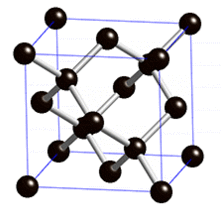
Along an appropriate axis, the lattice has six-fold symmetry (hexagonal).

Canonical Diamond

A canonical diamond lattice (single atom/particle type arranged as shown above) has symmetry Fd3m. The atoms occupy the positions (0,0,0;1/4,1/4,1/4)+face-centering.

Symmetry

• Crystal Family: Cubic
• Crystal System: Cubic
• Bravais Lattice: F (fcc)
• Crystal class: Hexoctahedral
• Point Group: d3m
• Space Group: Fd3m
• Particles per unit cell: $n=8$
• Volume of unit cell: $V_{d}=a^{3}$
• Dimensionality: $d=3$
• Projected d-dimensional volume: $v_{d}=a^{3}$
• Solid angle: $\Omega _{d}=4\pi$
• Nearest-neighbor distance: $d_{nn}={\sqrt {3}}a/4\approx 0.433a$
• Assuming spherical particles of radius R:
  • Particle volume fraction: $\phi =32\pi R^{3}/\left(3a^{3}\right)$
  • Maximum volume fraction: $\phi _{max}=\pi {\sqrt {3}}/16\approx 0.340$ when $R=a{\sqrt {3}}/8$

Structure

The lattice may be thought of as two interpenetrating FCC lattices.

Particle Positions

There are 18 positions. In total there are 8 particles in the unit cell:

• $8\,\mathrm {corners} \,\times \,{\frac {1}{8}}=1$
  • $\left(0,0,0\right),(0,0,1),(0,1,0),(1,0,0),(0,1,1),(1,0,1),(1,1,0),(1,1,1)$
• $6\,\mathrm {faces} \,\times \,{\frac {1}{2}}=3$
  • $\left(0,{\frac {1}{2}},{\frac {1}{2}}\right),\left({\frac {1}{2}},0,{\frac {1}{2}}\right),\left({\frac {1}{2}},{\frac {1}{2}},0\right),\left(1,{\frac {1}{2}},{\frac {1}{2}}\right),\left({\frac {1}{2}},1,{\frac {1}{2}}\right),\left({\frac {1}{2}},{\frac {1}{2}},1\right)$
• $4\,\mathrm {internal\,\,tetrahedral\,\,sites} \,\times \,1=4$
  • $\left({\frac {1}{4}},{\frac {1}{4}},{\frac {1}{4}}\right)+(0,0,0)=\left({\frac {1}{4}},{\frac {1}{4}},{\frac {1}{4}}\right)$
  • $\left({\frac {1}{4}},{\frac {1}{4}},{\frac {1}{4}}\right)+\left(0,{\frac {1}{2}},{\frac {1}{2}}\right)=\left({\frac {1}{4}},{\frac {3}{4}},{\frac {3}{4}}\right)$
  • $\left({\frac {1}{4}},{\frac {1}{4}},{\frac {1}{4}}\right)+\left({\frac {1}{2}},0,{\frac {1}{2}}\right)=\left({\frac {3}{4}},{\frac {1}{4}},{\frac {3}{4}}\right)$
  • $\left({\frac {1}{4}},{\frac {1}{4}},{\frac {1}{4}}\right)+\left({\frac {1}{2}},{\frac {1}{2}},0\right)=\left({\frac {3}{4}},{\frac {3}{4}},{\frac {1}{4}}\right)$

Examples

Elemental

6. Carbon (C) (a = 3.567 Å)

14. Silicon (Si) (a = 5.431 Å)

32. Germanium (Ge) (a = 5.657 Å)

50. Gray Tin (Sn) (a = 6.491 Å)

Atomic

• TBD

Nano

• Nanoparticle superlattice
  • Liu, W.; Tagawa, M.; Xin, H.L.; Wang, T.; Emamy, H. Li, H.; Yager, K.G.; Starr, F.W.; Tkachenko, A.V.; Gang, O. Diamond family of nanoparticle superlattices Science 2016, 351, 582–586. doi: 10.1126/science.aad2080

Diamond-like Two-particle

Also known as zincblende. This is effectively

Examples

Atomics

• Gallium arsenide (GaAs)
• Zinc sulfide (ZnS), a.k.a. zincblende
• Indium phosphide (InP)
• Cubic silicon carbide (CSi)
• Cubic gallium nitride (GaN)

Double-filled Diamond-like Two-particle

The diamond lattice includes 8 "tetrahedral holes", with only 4 occupied in a 'normal' diamond structure. A two-particle lattice can be formed by filling all 8 internal holes with the 2nd particle-type, in which case the particles exist in a 1:2 ratio. This is often called a CaF₂ lattice.

Particle Positions

There are 22 positions. In total there are 12 particles in the unit cell:

• $8\,\mathrm {corners} \,\times \,{\frac {1}{8}}=1$
  • $\left(0,0,0\right),(0,0,1),(0,1,0),(1,0,0),(0,1,1),(1,0,1),(1,1,0),(1,1,1)$
• $6\,\mathrm {faces} \,\times \,{\frac {1}{2}}=3$
  • $\left(0,{\frac {1}{2}},{\frac {1}{2}}\right),\left({\frac {1}{2}},0,{\frac {1}{2}}\right),\left({\frac {1}{2}},{\frac {1}{2}},0\right),\left(1,{\frac {1}{2}},{\frac {1}{2}}\right),\left({\frac {1}{2}},1,{\frac {1}{2}}\right),\left({\frac {1}{2}},{\frac {1}{2}},1\right)$
• $4\,\mathrm {principal\,\,tetrahedral\,\,sites} \,\times \,1=4$
  • $\left({\frac {1}{4}},{\frac {1}{4}},{\frac {1}{4}}\right)+(0,0,0)=\left({\frac {1}{4}},{\frac {1}{4}},{\frac {1}{4}}\right)$
  • $\left({\frac {1}{4}},{\frac {1}{4}},{\frac {1}{4}}\right)+\left(0,{\frac {1}{2}},{\frac {1}{2}}\right)=\left({\frac {1}{4}},{\frac {3}{4}},{\frac {3}{4}}\right)$
  • $\left({\frac {1}{4}},{\frac {1}{4}},{\frac {1}{4}}\right)+\left({\frac {1}{2}},0,{\frac {1}{2}}\right)=\left({\frac {3}{4}},{\frac {1}{4}},{\frac {3}{4}}\right)$
  • $\left({\frac {1}{4}},{\frac {1}{4}},{\frac {1}{4}}\right)+\left({\frac {1}{2}},{\frac {1}{2}},0\right)=\left({\frac {3}{4}},{\frac {3}{4}},{\frac {1}{4}}\right)$
• $4\,\mathrm {tetrahedral\,\,holes} \,\times \,1=4$
  • $\left({\frac {3}{4}},{\frac {3}{4}},{\frac {3}{4}}\right)-(0,0,0)=\left({\frac {3}{4}},{\frac {3}{4}},{\frac {3}{4}}\right)$
  • $\left({\frac {3}{4}},{\frac {3}{4}},{\frac {3}{4}}\right)-\left(0,{\frac {1}{2}},{\frac {1}{2}}\right)=\left({\frac {3}{4}},{\frac {1}{4}},{\frac {1}{4}}\right)$
  • $\left({\frac {3}{4}},{\frac {3}{4}},{\frac {3}{4}}\right)-\left({\frac {1}{2}},0,{\frac {1}{2}}\right)=\left({\frac {1}{4}},{\frac {3}{4}},{\frac {1}{4}}\right)$
  • $\left({\frac {3}{4}},{\frac {3}{4}},{\frac {3}{4}}\right)-\left({\frac {1}{2}},{\frac {1}{2}},0\right)=\left({\frac {1}{4}},{\frac {1}{4}},{\frac {3}{4}}\right)$

Neighbors

There are 12 particles in the unit cell: 4 of type A, and 8 of type B. The type A particles each connect to 8 particles of type B. The type B particles each connect (tetrahedrally) to 4 particles of type A.

The lattice may also be thought of as having cubes of type B with a connected type A particle at the center. However the extended lattice is not BCC-like, since only every second "BCC cube" has a central particle of type A.

Examples

Atomics

• Calcium fluoride (CaF₂) (a = 5.46 Å)

Double Inter-penetrating Diamond Two-Particle

This lattice is formed from two diamond lattices that inter-penetrate. It is often called the NaTl lattice.

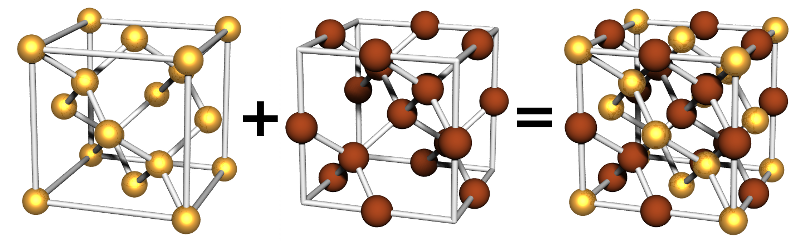
Particle Positions

There are 36 positions. In total there are 16 particles in the unit cell, 8 of each type.

Particle Type A

• $8\,\mathrm {corners} \,\times \,{\frac {1}{8}}=1$
  • $\left(0,0,0\right),(0,0,1),(0,1,0),(1,0,0),(0,1,1),(1,0,1),(1,1,0),(1,1,1)$
• $6\,\mathrm {faces} \,\times \,{\frac {1}{2}}=3$
  • $\left(0,{\frac {1}{2}},{\frac {1}{2}}\right),\left({\frac {1}{2}},0,{\frac {1}{2}}\right),\left({\frac {1}{2}},{\frac {1}{2}},0\right),\left(1,{\frac {1}{2}},{\frac {1}{2}}\right),\left({\frac {1}{2}},1,{\frac {1}{2}}\right),\left({\frac {1}{2}},{\frac {1}{2}},1\right)$
• $4\,\mathrm {internal\,\,tetrahedral\,\,sites} \,\times \,1=4$
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{1}{4},\frac{1}{4},\frac{1}{4}\right)+(0,0,0)=\left(\frac{1}{4},\frac{1}{4},\frac{1}{4}\right)}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{1}{4},\frac{1}{4},\frac{1}{4}\right)+\left(0,\frac{1}{2},\frac{1}{2}\right)=\left(\frac{1}{4},\frac{3}{4},\frac{3}{4}\right)}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{1}{4},\frac{1}{4},\frac{1}{4}\right)+\left(\frac{1}{2},0,\frac{1}{2}\right)=\left(\frac{3}{4},\frac{1}{4},\frac{3}{4}\right)}
  • $\left({\frac {1}{4}},{\frac {1}{4}},{\frac {1}{4}}\right)+\left({\frac {1}{2}},{\frac {1}{2}},0\right)=\left({\frac {3}{4}},{\frac {3}{4}},{\frac {1}{4}}\right)$

Particle Type B

• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 12 \, \mathrm{edges} \, \times \, \frac{1}{4} = 3}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{1}{2},0,0\right) , \left(0,\frac{1}{2},0\right) , \left(0,0,\frac{1}{2}\right) }
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(1,0,\frac{1}{2}\right) , \left(1,1,\frac{1}{2}\right) , \left(0,1,\frac{1}{2}\right) , \left(\frac{1}{2},1,0\right) , \left(1,\frac{1}{2},0\right) , \left(\frac{1}{2},0,1\right) , \left(0,\frac{1}{2},1\right), \left(1,\frac{1}{2},1\right) , \left(\frac{1}{2},1,1\right) }
• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 \, \mathrm{central} \, \times \, 1 = 1}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{1}{2},\frac{1}{2},\frac{1}{2}\right) }
• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4 \, \mathrm{internal \,\, tetrahedral \,\, sites} \, \times \, 1 = 4}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{3}{4},\frac{3}{4},\frac{3}{4}\right)-(0,0,0)=\left(\frac{3}{4},\frac{3}{4},\frac{3}{4}\right)}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{3}{4},\frac{3}{4},\frac{3}{4}\right)-\left(0,\frac{1}{2},\frac{1}{2}\right)=\left(\frac{3}{4},\frac{1}{4},\frac{1}{4}\right)}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{3}{4},\frac{3}{4},\frac{3}{4}\right)-\left(\frac{1}{2},0,\frac{1}{2}\right)=\left(\frac{1}{4},\frac{3}{4},\frac{1}{4}\right)}
  • $\left({\frac {3}{4}},{\frac {3}{4}},{\frac {3}{4}}\right)-\left({\frac {1}{2}},{\frac {1}{2}},0\right)=\left({\frac {1}{4}},{\frac {1}{4}},{\frac {3}{4}}\right)$

Examples

Atomics

• Sodium Thallium crystal (NaTl)

Nanoparticles

• Au NPs and proteins: Petr Cigler, Abigail K. R. Lytton-Jean, Daniel G. Anderson, M. G. Finn & Sung Yong Park DNA-controlled assembly of a NaTl lattice structure from gold nanoparticles and protein nanoparticles Nature Materials 9, 918–922 (2010) doi:10.1038/nmat2877

  

Cristobalite

Cristobalite is a diamond-like lattice formed in silicon dioxide (SiO₂). The Si atoms bond tetradrally, each to four O atoms. Each O atom is bonded to 2 Si atoms, effectively acting as a bridge.

Structure

Can be thought of as a diamond lattice, where the tetrahedral species sit on the positions of the canonical diamond sites, and the two-bonded species sites at the midway point of each bond.

The tetrahedral species sit on the 14 "FCC" sites, plus 4 "internal" diamond sites. The two-bonded species sit on the 16 internal bonds in the unit cell. The tetrahedral species sit at a distance from one another of:

• Next-nearest-neighbor distance: $d_{nnn}={\sqrt {3}}a/4\approx 0.433a$

The different species thus have a distance of half that:

• Nearest-neighbor distance: Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d_{nn}=\sqrt{3}a/8 \approx 0.217 a}

Particle Positions

There are 34 positions (24 in unit cell)

Particle Type A (bond tetrahedrally)

There are 18 positions. In total there are 8 particles in the unit cell:

• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 8 \, \mathrm{corners} \, \times \, \frac{1}{8} = 1}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(0,0,0\right),(0,0,1),(0,1,0),(1,0,0),(0,1,1),(1,0,1),(1,1,0),(1,1,1)}
• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6 \, \mathrm{faces} \, \times \, \frac{1}{2} = 3}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(0,\frac{1}{2},\frac{1}{2}\right),\left(\frac{1}{2},0,\frac{1}{2}\right),\left(\frac{1}{2},\frac{1}{2},0\right),\left(1,\frac{1}{2},\frac{1}{2}\right),\left(\frac{1}{2},1,\frac{1}{2}\right),\left(\frac{1}{2},\frac{1}{2},1\right)}
• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4 \, \mathrm{internal \,\, tetrahedral \,\, sites} \, \times \, 1 = 4}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{1}{4},\frac{1}{4},\frac{1}{4}\right)+(0,0,0)=\left(\frac{1}{4},\frac{1}{4},\frac{1}{4}\right)}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{1}{4},\frac{1}{4},\frac{1}{4}\right)+\left(0,\frac{1}{2},\frac{1}{2}\right)=\left(\frac{1}{4},\frac{3}{4},\frac{3}{4}\right)}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{1}{4},\frac{1}{4},\frac{1}{4}\right)+\left(\frac{1}{2},0,\frac{1}{2}\right)=\left(\frac{3}{4},\frac{1}{4},\frac{3}{4}\right)}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{1}{4},\frac{1}{4},\frac{1}{4}\right)+\left(\frac{1}{2},\frac{1}{2},0\right)=\left(\frac{3}{4},\frac{3}{4},\frac{1}{4}\right)}

Particle Type B (two-fold bonded)

There are 16 positions (all 16 in the unit cell):

• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4 \, \mathrm{level \,\, one} \, \times \, 1 = 4}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{ (0,0,0)+\left(\frac{1}{4},\frac{1}{4},\frac{1}{4}\right) }{2} =\left(\frac{1}{8},\frac{1}{8},\frac{1}{8}\right)}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{ \left(\frac{1}{4},\frac{1}{4},\frac{1}{4}\right)+\left(\frac{1}{2},\frac{1}{2},0 \right) }{2} =\left(\frac{3}{8},\frac{3}{8},\frac{1}{8}\right)}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{ \left(\frac{1}{2},\frac{1}{2},0 \right) + \left(\frac{3}{4},\frac{3}{4},\frac{1}{4}\right) }{2} =\left(\frac{5}{8},\frac{5}{8},\frac{1}{8}\right)}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{ \left(\frac{3}{4},\frac{3}{4},\frac{1}{4}\right) + (1,1,0) }{2} =\left(\frac{7}{8},\frac{7}{8},\frac{1}{8}\right)}
• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4 \, \mathrm{level \,\, two} \, \times \, 1 = 4}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{ \left(\frac{1}{4},\frac{1}{4},\frac{1}{4} \right) + \left(\frac{1}{2},0,\frac{1}{2} \right) }{2} =\left(\frac{3}{8},\frac{1}{8},\frac{3}{8}\right)}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{ \left(\frac{1}{4},\frac{1}{4},\frac{1}{4} \right) + \left(0,\frac{1}{2},\frac{1}{2} \right) }{2} =\left(\frac{1}{8},\frac{3}{8},\frac{3}{8}\right)}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{ \left(\frac{3}{4},\frac{3}{4},\frac{1}{4} \right) + \left(1,\frac{1}{2},\frac{1}{2} \right) }{2} =\left(\frac{7}{8},\frac{5}{8},\frac{3}{8}\right)}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{ \left(\frac{3}{4},\frac{3}{4},\frac{1}{4} \right) + \left(\frac{1}{2},1,\frac{1}{2} \right) }{2} =\left(\frac{5}{8},\frac{7}{8},\frac{3}{8}\right)}
• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4 \, \mathrm{level \,\, three} \, \times \, 1 = 4}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{ \left(\frac{3}{4},\frac{1}{4},\frac{3}{4} \right) + \left(\frac{1}{2},0,\frac{1}{2} \right) }{2} =\left(\frac{5}{8},\frac{1}{8},\frac{5}{8}\right)}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{ \left(\frac{3}{4},\frac{1}{4},\frac{3}{4} \right) + \left(1,\frac{1}{2},\frac{1}{2} \right) }{2} =\left(\frac{7}{8},\frac{3}{8},\frac{5}{8}\right)}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{ \left(\frac{1}{4},\frac{3}{4},\frac{3}{4} \right) + \left(0,\frac{1}{2},\frac{1}{2} \right) }{2} =\left(\frac{1}{8},\frac{5}{8},\frac{5}{8}\right)}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{ \left(\frac{1}{4},\frac{3}{4},\frac{3}{4} \right) + \left(\frac{1}{2},1,\frac{1}{2} \right) }{2} =\left(\frac{3}{8},\frac{7}{8},\frac{5}{8}\right)}
• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4 \, \mathrm{level \,\, four} \, \times \, 1 = 4}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{ (1,0,1) + \left(\frac{3}{4},\frac{1}{4},\frac{3}{4}\right) }{2} =\left(\frac{7}{8},\frac{1}{8},\frac{7}{8}\right)}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{ \left(\frac{3}{4},\frac{1}{4},\frac{3}{4}\right) + \left(\frac{1}{2},\frac{1}{2},1 \right) }{2} =\left(\frac{5}{8},\frac{3}{8},\frac{7}{8}\right)}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{ \left(\frac{1}{2},\frac{1}{2},1 \right) + \left(\frac{1}{4},\frac{3}{4},\frac{3}{4}\right) }{2} =\left(\frac{3}{8},\frac{5}{8},\frac{7}{8}\right)}
  • Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{ \left(\frac{1}{4},\frac{3}{4},\frac{3}{4} \right) + (0,1,1) }{2} =\left(\frac{1}{8},\frac{7}{8},\frac{7}{8}\right)}

Examples

Atomics

• Cristobalite form of silicon dioxide (SiO₂)

See Also

• Diamond Cubic (Wikipedia)
• Hexagonal Diamond Lattice