Absorption length

The absorption length or attenuation length in x-ray scattering is the distance over which the x-ray beam is absorbed. By convention, the absorption length ϵ is defined as the distance into a material where the beam flux has dropped to 1/e of its incident flux.

Absorption

The absorption follows a simple Beer-Lambert law:

{\frac {I(x)}{I_{0}}}=e^{-x/\epsilon }

The attenuation coefficient (or absorption coefficient) is simply the inverse of the absorption length; Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu = 1/\epsilon}

{\frac {I(x)}{I_{0}}}=e^{-\mu x}

Calculating

The absorption length arises from the imaginary part of the atomic scattering factor, f₂. It is closely related to the absorption cross-section, and the mass absorption coefficient. Specifically, the atomic photoabsorption cross-section can be computed via:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sigma = 2 r_e \lambda f_2 }

Where λ is the x-ray wavelength, and r_e is the classical electron radius. The attenuation coefficient is given by:

{\begin{alignedat}{2}\mu &={\frac {\rho N_{a}}{m_{a}}}\sigma \\&={\frac {\rho N_{a}}{m_{a}}}2r_{e}\lambda f_{2}\end{alignedat}}

where ρ is density, N_a is the Avogadro constant, and m_a is the atomic molar mass. Note that the mass attenuation coefficient is simply $\mu /\rho$ .

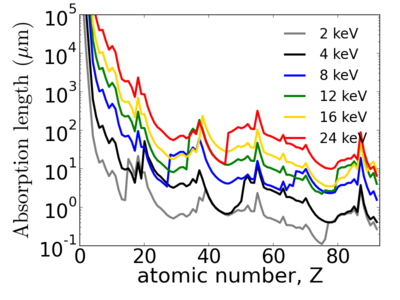
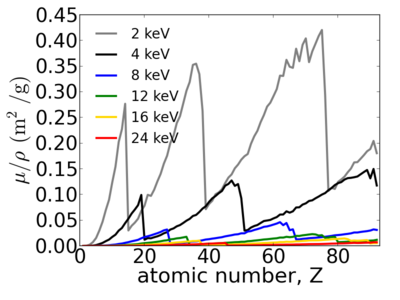
Elemental dependence

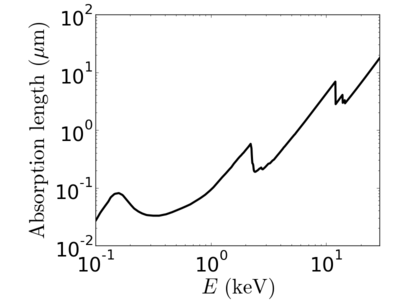
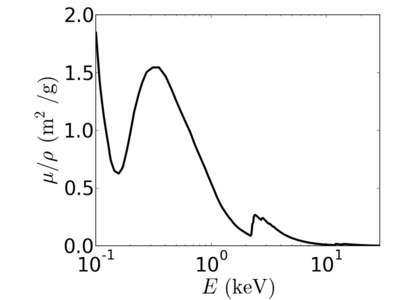
Energy dependence

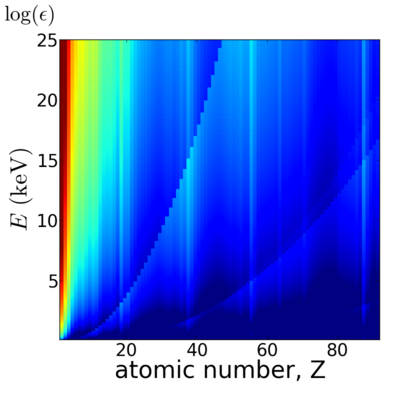
Notice that the absorption undergoes sharp increases when passing through an absorption edge.

Examples

silicon

gold

Elemental/Energy dependence

Related forms

As can be seen, there are many related quantities which express the material's absorption:

Absorption length $\epsilon$ , the distance over which the intensity falls to 1/e.
Attenuation coefficient $\mu$ , the characteristic inverse-distance for attenuation.
Mass attenuation coefficient $\mu /\rho$ , the density-scaled attenuation.
Absorptive atomic scattering factor $f_{2}$ , the intrinsic dissipative interaction of the material.
Atomic photoabsorption cross-section $\sigma$ , the cross-section ('effective size') of the atom's x-ray absorption (capture) efficiency.
Imaginary refractive index $\beta$ , the resonant component of the refractive index.
Imaginary Scattering Length Density $\mathrm {Im} (\mathrm {SLD} )$ , the absorptive component of the scattering contrast.

$\epsilon$	$\epsilon ={\frac {1}{\mu }}$	$\epsilon ={\frac {\rho }{\mu /\rho }}$	$\epsilon ={\frac {M_{a}}{\rho N_{a}2r_{e}\lambda f_{2}}}$	$\epsilon ={\frac {M_{a}}{\rho N_{a}\sigma }}$	$\epsilon ={\frac {\lambda }{4\pi \beta }}$	$\epsilon ={\frac {1}{2\lambda \mathrm {Im} (\mathrm {SLD} )}}$
$\mu ={\frac {1}{\epsilon }}$	$\mu$	$\mu ={\frac {\mu /\rho }{\rho }}$	$\mu ={\frac {\rho N_{a}}{M_{a}}}2r_{e}\lambda f_{2}$	$\mu ={\frac {\rho N_{a}}{M_{a}}}\sigma$	$\mu ={\frac {4\pi }{\lambda }}\beta$	$\mu =2\lambda \mathrm {Im} (\mathrm {SLD} )$
${\frac {\mu }{\rho }}={\frac {1}{\rho \epsilon }}$	${\frac {\mu }{\rho }}=\mu /\rho$	${\frac {\mu }{\rho }}$	${\frac {\mu }{\rho }}={\frac {N_{a}}{M_{a}}}2r_{e}\lambda f_{2}$	${\frac {\mu }{\rho }}={\frac {N_{a}}{M_{a}}}\sigma$	${\frac {\mu }{\rho }}={\frac {4\pi }{\rho \lambda }}\beta$	${\frac {\mu }{\rho }}={\frac {2\lambda }{\rho }}\mathrm {Im} (\mathrm {SLD} )$
$f_{2}={\frac {M_{a}}{\rho N_{a}2r_{e}\lambda \epsilon }}$	$f_{2}={\frac {M_{a}}{\rho N_{a}2r_{e}\lambda }}\mu$	$f_{2}={\frac {M_{a}}{N_{a}2r_{e}\lambda }}{\frac {\mu }{\rho }}$	$f_{2}$	$f_{2}={\frac {\sigma }{2r_{e}\lambda }}$	$f_{2}={\frac {2\pi M_{a}}{\rho N_{a}r_{e}\lambda ^{2}}}\beta$	$f_{2}={\frac {M_{a}}{\rho N_{a}r_{e}}}\mathrm {Im} (\mathrm {SLD} )$
$\sigma ={\frac {M_{a}}{\rho N_{a}\epsilon }}$	$\sigma ={\frac {M_{a}}{\rho N_{a}}}\mu$	$\sigma ={\frac {M_{a}}{N_{a}}}{\frac {\mu }{\rho }}$	$\sigma =2r_{e}\lambda f_{2}$	$\sigma$	$\sigma ={\frac {4\pi M_{a}}{\rho N_{a}\lambda }}\beta$	$\sigma ={\frac {2\lambda M_{a}}{\rho N_{a}}}\mathrm {Im} (\mathrm {SLD} )$
$\beta ={\frac {\lambda }{4\pi \epsilon }}$	$\beta ={\frac {\lambda }{4\pi }}\mu$	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = \frac{ \rho \lambda }{4 \pi } \frac{\mu}{\rho}}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = \frac{ \rho N_a r_e \lambda^2 }{2 \pi M_a} f_2}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = \frac{ \rho N_a \lambda }{4 \pi M_a} \sigma}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = \frac{\lambda^2}{2 \pi} \mathrm{Im}(\mathrm{SLD})}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{Im}(\mathrm{SLD}) = \frac{1 }{2 \lambda \epsilon} }	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{Im}(\mathrm{SLD}) = \frac{\mu}{2 \lambda} }	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{Im}(\mathrm{SLD}) = \frac{\rho }{2 \lambda} \frac{\mu}{\rho}}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{Im}(\mathrm{SLD}) = \frac{\rho N_a r_e }{M_a} f_2}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{Im}(\mathrm{SLD}) = \frac{\rho N_a}{2 \lambda M_a}\sigma}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{Im}(\mathrm{SLD}) = \frac{2 \pi }{\lambda^2} \beta}	Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathrm{Im}(\mathrm{SLD})}