Integrated intensity

From GISAXS
Jump to: navigation, search

The following describes how to think about integrated peak intensity (in reciprocal-space) in order to estimate the amount of material giving rise to the observed scattering peak.

General Form

The integrated intensity in reciprocal-space arising from a particular peak is proportional to the quantity (strictly, scattering volume) of the ordered structure that produces the scattering peak. In order to quantify the amount of an ordered population (e.g. a crystalline component), one must integrate over the entirety of reciprocal-space the intensity for the given peak.

In the most general case, let us denote the intensity of the peak in reciprocal space by the function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I_p(\mathbf{q})} . The full intensity of the peak is then:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{alignat}{2} I_{\mathrm{total}} = \int\int\int I_p(\mathbf{q}) \mathrm{d}V \end{alignat} }

Of course the integration can be performed in whatever coordinate system is most convenient. For instance Cartesian coordinates:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{alignat}{2} I_{\mathrm{total}} = \int_{q_x=-\infty}^{\infty}\int_{q_y=-\infty}^{\infty}\int_{q_z=-\infty}^{\infty} I_p(q_x,q_y,q_z) \mathrm{d}q_z\mathrm{d}q_y\mathrm{d}q_x \end{alignat} }

Or by converting to spherical coordinates Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(q,\omega,\phi\right)} using:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{alignat}{2} q & = \left| \mathbf{q} \right| = \sqrt{q_x^2+q_y^2+q_z^2} \\ \omega & = \cos^{-1}\left( \frac{q_z}{q} \right) \\ \phi & = \tan^{-1}\left( \frac{q_y}{q_x} \right) \end{alignat} }

It becomes:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{alignat}{2} I_{\mathrm{total}} = \int_{\phi=-0}^{2 \pi}\int_{\omega=0}^{\pi}\int_{q=0}^{\infty} I_p(q,\omega,\phi) q^2 \sin\omega \mathrm{d}q\mathrm{d}\omega\mathrm{d}\phi \end{alignat} }
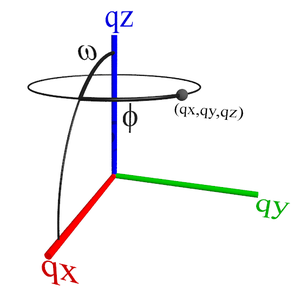
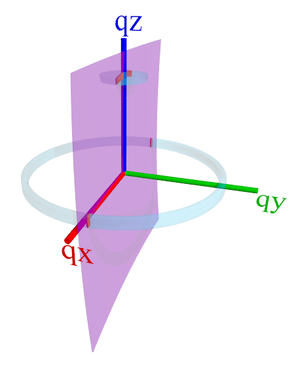
Coordinate system for spherical coordinates in reciprocal-space.


The peak of interest is localized near a particular q-value. This implies that spherical symmetry will be useful for integration. Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_{0}} be the peak center position, and let us decompose the distribution of the peak into a peak shape along the q-direction, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L(q)} , and an orientation distribution given by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega(\omega,\phi)} . We would then write:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{alignat}{2} I_{\mathrm{total}} & = \int_{0}^{2 \pi}\int_{0}^{\pi}\int_{0}^{\infty} I_{0} L(q) \Omega(\omega,\phi) q^2 \sin\omega \mathrm{d}q\mathrm{d}\omega\mathrm{d}\phi \\ & = I_{0} \int_{0}^{\infty} L(q) q^2 \mathrm{d}q \int_{0}^{2 \pi}\int_{0}^{\pi} \Omega(\omega,\phi) \sin\omega \mathrm{d}\omega\mathrm{d}\phi \end{alignat} }

In practice peaks are usually relatively sharp, so that we need only integrate within a small region, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \delta q} near Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_0} , in which case one can assume Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q\approx q_0} over the integration:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{alignat}{2} I_{\mathrm{total}} & \approx I_{0} \int_{q_{0}-\delta q}^{q_{0}+\delta q} L(q) q^2 \mathrm{d}q \int_{0}^{2 \pi}\int_{0}^{\pi} \Omega(\omega,\phi) \sin\omega \mathrm{d}\omega\mathrm{d}\phi \\ & \approx I_{0} q_0^2 \int_{q_{0}-\delta q}^{q_{0}+\delta q} L(q) \mathrm{d}q \int_{0}^{2 \pi}\int_{0}^{\pi} \Omega(\omega,\phi) \sin\omega \mathrm{d}\omega\mathrm{d}\phi \end{alignat} }

Powder Analysis

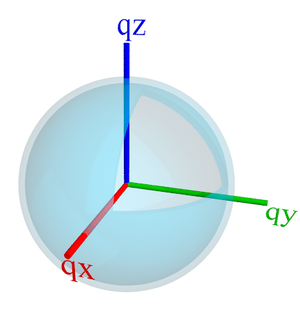
Scattering intensity in reciprocal-space for an isotropic powder. The cutout is only to help visualize that the scattering is a thin shell of uniform intensity.

Consider a measurement of an isotropic powder. In reciprocal-space, the scattering peak of interest is spread uniformly over a 'shell' at the position Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q=q_0} . A measurement using a 2D detector, however, will only show a slice through this three-dimensional scattering space. A 2D slice of a 3D shell is a ring of uniform scattering intensity. In order to get the total integrated intensity for the peak, we can take advantage of the fact that the scattering is isotropic, such that:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{alignat}{2} \Omega\left(\omega,\phi\right) = c \end{alignat} }

Where c is a constant. (A normalized version of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega(\omega,\phi)} would have Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c=1/(4\pi)} .) In such a case:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{alignat}{2} I_{\mathrm{total}} & = \int_{0}^{2 \pi}\int_{0}^{\pi}\int_{q_{0}-\delta q}^{q_{0} + \delta q} I_{0} L(q) \Omega(\omega,\phi) q^2 \sin\omega \mathrm{d}q\mathrm{d}\omega\mathrm{d}\phi \\ & = I_{0} \int_{q_{0}-\delta q}^{q_{0} + \delta q} L(q) q^2 \mathrm{d}q \left[ \int_{0}^{2 \pi} \int_{0}^{\pi} c \sin\omega \mathrm{d}\omega\mathrm{d}\phi \right] \\ & = I_{0} \int_{q_{0}-\delta q}^{q_{0} + \delta q} L(q) q^2 \mathrm{d}q \left[ c \int_{0}^{\pi} \sin\omega \mathrm{d}\omega \int_{0}^{2 \pi} \mathrm{d}\phi \right] \\ & = I_{0} \int_{q_{0}-\delta q}^{q_{0} + \delta q} L(q) q^2 \mathrm{d}q \left[ c \times 2 \times 2 \pi \right] \\ & = I_{0} c 4 \pi \int_{q_{0}-\delta q}^{q_{0} + \delta q} L(q) q^2 \mathrm{d}q \\ & \approx I_{0} c 4 \pi q_0^2 \int L(q) \mathrm{d}q \end{alignat} }

The spherical coordinate integration factors (in particular Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin\omega} ) disappear because the orientation distribution does not depend on angle (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} ). In other words, the relationship between the intensity measured on the detector and the integrated intensity is simply the surface area (in reciprocal space) of the spherical shell of scattering intensity (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S=4\pi q_0^2} ).


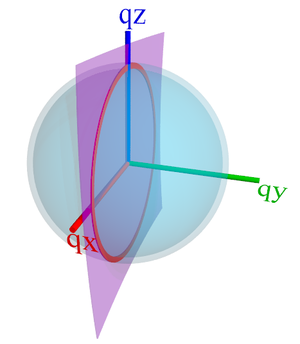
The intersection of the Ewald sphere (purple sheet) with the scattering intensity (light-blue shell) produces a ring of uniform intensity (red ring) on the detector. Correct integration of this ring yields the intensity of the entire scattering shell, by taking advantage of the isotropic symmetry.

Thin Film with In-Plane Isotropy

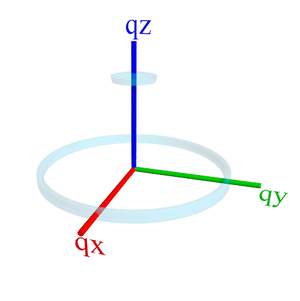
Example of the scattering intensity in reciprocal-space for a thin film that is 'in-plane isotropic'. In this example, there is some intensity from the scattering peak along the qz axis (e.g. from horizontal crystal planes) and intensity in a ring around the qx-qy plane (e.g. from a population of vertical crystal planes with no in-plane preferential orientation).


In the general case the only way to determine the full integrated intensity is to scan the Ewald sphere and reconstruct the entire reciprocal space (e.g. by rotating the sample in-plane). However one can also take advantage of known symmetries of the sample. In the example above, for an isotropic powder, calculating the integrated intensity can be in fact be performed with a single line-scan along q.

For a thin film that is isotropic in-plane, a rotation about the film normal axis (changing angle Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} ) would give the same detector pattern repeatedly. We can take advantage of this symmetry by aligning the spherical coordinate system with Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q_z} pointed along the film normal direction. Thus instead of rotating the sample physically about Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} , we can use the measured intensity distribution along a single Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} -arc, and integrate along Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} mathematically.

In other words, the in-plane isotropy guarantees that:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{alignat}{2} \Omega\left(\omega,\phi\right) = \Omega(\omega) \end{alignat} }

Such that:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{alignat}{2} I_{\mathrm{total}} & = \int_{0}^{2 \pi}\int_{0}^{\pi}\int_{q_{0}-\delta q}^{q_{0} + \delta q} I_{0} L(q) \Omega(\omega,\phi) q^2 \sin\omega \mathrm{d}q\mathrm{d}\omega\mathrm{d}\phi \\ & = I_{0} \int_{q_{0}-\delta q}^{q_{0} + \delta q} L(q) q^2 \mathrm{d}q \int_{0}^{2 \pi}\int_{0}^{\pi} \Omega(\omega) \sin\omega \mathrm{d}\omega\mathrm{d}\phi \\ & = I_{0} \int_{q_{0}-\delta q}^{q_{0} + \delta q} L(q) q^2 \mathrm{d}q \int_{0}^{\pi} \Omega(\omega) \sin\omega \mathrm{d}\omega \int_{0}^{2 \pi} \mathrm{d}\phi \\ & = I_{0} 2 \pi \int_{q_{0}-\delta q}^{q_{0} + \delta q} L(q) q^2 \mathrm{d}q \int_{0}^{\pi} \Omega(\omega) \sin\omega \mathrm{d}\omega \end{alignat} }

Thus to obtain the integrated intensity (which is proportional to the amount of 'ordered' material) one can use a single measurement of the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega} -arc (to get the distribution function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Omega(\omega)} ) and integrate using the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin\omega} integration factor.


The intersection of the Ewald sphere (purple sheet) with the scattering intensity (light-blue volumes) produces scattering peaks (red) on the detector. Correct integration of these peaks yields the full intensity in reciprocal-space by taking advantage of the in-plane isotropic symmetry. The scattering peak observed along the qz axis represents a smaller population of grains than the scattering peak appearing along the qx axis.

Effect of Resolution Function

The resolution of a given measurement has a dramatic effect on the peak shapes seen on the detector. Peak broadening also occurs in directions normal to the detector surface, such that some intensity falls outside the slice that the detector captures. In order to quantitatively compare the intensity measured on a detector with either theory or another intensity measurement, one must account for these resolution effects.

Note, however, that the effect of the resolution function is to 'smear' the intensity in reciprocal-space. Conceptually, each point in reciprocal-space has its intensity spread out over a certain region (e.g. an ellipsoid). However the total scattering intensity is unchanged. In this sense, performing an integration is inherently insensitive to any resolution effects, so long as the integration is large enough to fully capture the broadened peak. The 'broadening' includes both the local spread of a peak due to resolution effects, as well as the distribution of the scattering intensity over a shell in reciprocal space due to the orientation distribution of the grains in the material.

Thus, when comparing sub-sections of scattered intensity, the resolution correction must be included. But when comparing the total integrated intensity, any such correction would disappear because by definition we are integrating all the intensity arising from a particular scattering peak.

Retrieved from "http://gisaxs.com/index.php?title=Integrated_intensity&oldid=4714"