Difference between revisions of "Absorption length"
KevinYager (talk | contribs) (→Calculating) |
KevinYager (talk | contribs) (→See Also) |
||
| (28 intermediate revisions by the same user not shown) | |||
| Line 24: | Line 24: | ||
</math> | </math> | ||
where ''ρ'' is density, ''N<sub>a</sub>'' is the Avogadro constant, and ''m<sub>a</sub>'' is the atomic molar mass. Note that the '''mass attenuation coefficient''' is simply <math>\mu/\rho</math>. | where ''ρ'' is density, ''N<sub>a</sub>'' is the Avogadro constant, and ''m<sub>a</sub>'' is the atomic molar mass. Note that the '''mass attenuation coefficient''' is simply <math>\mu/\rho</math>. | ||
| + | |||
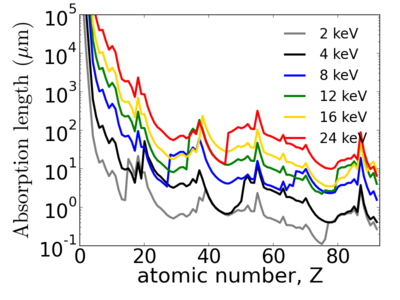
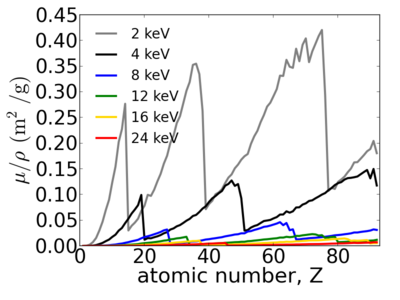
| + | ==Elemental dependence== | ||
| + | |||
| + | [[Image:Elements-abs.png|400px]][[Image:Elements-mu.png|400px]] | ||
| + | |||
| + | ==Energy dependence== | ||
| + | Notice that the absorption undergoes sharp increases when passing through an absorption edge. | ||
| + | |||
| + | ===Examples=== | ||
| + | |||
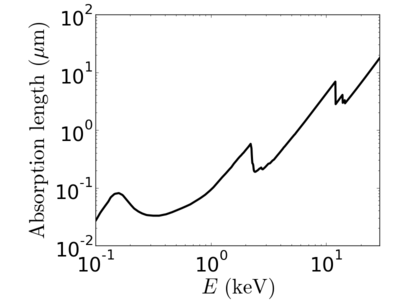
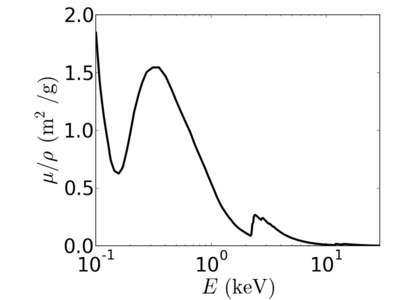
| + | ====[[Material:Silicon|silicon]]==== | ||
| + | |||
| + | [[Image:Silicon-AttLen.png|400px]][[Image:Silicon-mu.png|400px]] | ||
| + | |||
| + | ====[[Material:Gold|gold]]==== | ||
| + | |||
| + | [[Image:Gold-AttLen.png|400px]][[Image:Gold-mu.png|400px]] | ||
| + | |||
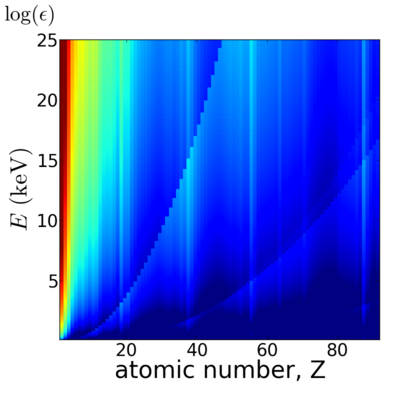
| + | ==Elemental/Energy dependence== | ||
| + | [[Image:Elements2D-abs.png|400px]][[Image:Elements2D-mu.png|400px]] | ||
==Related forms== | ==Related forms== | ||
| Line 34: | Line 54: | ||
* '''Imaginary [[refractive index]]''' <math>\beta</math>, the resonant component of the refractive index. | * '''Imaginary [[refractive index]]''' <math>\beta</math>, the resonant component of the refractive index. | ||
* '''Imaginary [[Scattering Length Density]]''' <math>\mathrm{Im}(\mathrm{SLD})</math>, the absorptive component of the scattering contrast. | * '''Imaginary [[Scattering Length Density]]''' <math>\mathrm{Im}(\mathrm{SLD})</math>, the absorptive component of the scattering contrast. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |||
| + | |- | ||
| + | | <math>\epsilon</math> | ||
| + | | <math>\epsilon = \frac{1}{\mu}</math> | ||
| + | | <math>\epsilon = \frac{\rho}{\mu/\rho}</math> | ||
| + | | <math>\epsilon = \frac{M_a}{\rho N_a 2 r_e \lambda f_2 }</math> | ||
| + | | <math>\epsilon = \frac{M_a}{\rho N_a \sigma}</math> | ||
| + | | <math>\epsilon = \frac{ \lambda }{4 \pi \beta}</math> | ||
| + | | <math>\epsilon = \frac{1}{2 \lambda \mathrm{Im}(\mathrm{SLD})} </math> | ||
| + | |- | ||
| + | | <math>\mu = \frac{1}{\epsilon}</math> | ||
| + | | <math>\mu</math> | ||
| + | | <math>\mu = \frac{\mu/\rho}{\rho}</math> | ||
| + | | <math>\mu = \frac{\rho N_a}{M_a} 2 r_e \lambda f_2</math> | ||
| + | | <math>\mu = \frac{\rho N_a}{M_a} \sigma</math> | ||
| + | | <math>\mu = \frac{4 \pi }{ \lambda } \beta</math> | ||
| + | | <math>\mu = 2 \lambda\mathrm{Im}(\mathrm{SLD})</math> | ||
| + | |- | ||
| + | | <math>\frac{\mu}{\rho} = \frac{1}{\rho\epsilon}</math> | ||
| + | | <math>\frac{\mu}{\rho} = \mu/\rho</math> | ||
| + | | <math>\frac{\mu}{\rho}</math> | ||
| + | | <math>\frac{\mu}{\rho} = \frac{N_a}{M_a} 2 r_e \lambda f_2</math> | ||
| + | | <math>\frac{\mu}{\rho} = \frac{N_a}{M_a} \sigma</math> | ||
| + | | <math>\frac{\mu}{\rho} = \frac{4 \pi}{ \rho \lambda } \beta</math> | ||
| + | | <math>\frac{\mu}{\rho} = \frac{2 \lambda}{\rho } \mathrm{Im}(\mathrm{SLD})</math> | ||
| + | |- | ||
| + | | <math>f_2 = \frac{M_a }{\rho N_a 2 r_e \lambda \epsilon} </math> | ||
| + | | <math>f_2 = \frac{M_a }{\rho N_a 2 r_e \lambda} \mu </math> | ||
| + | | <math>f_2 = \frac{M_a }{ N_a 2 r_e \lambda} \frac{\mu}{\rho} </math> | ||
| + | | <math>f_2</math> | ||
| + | | <math>f_2 = \frac{\sigma}{2 r_e \lambda}</math> | ||
| + | | <math>f_2 = \frac{2 \pi M_a}{ \rho N_a r_e \lambda^2 } \beta</math> | ||
| + | | <math>f_2 = \frac{M_a}{\rho N_a r_e } \mathrm{Im}(\mathrm{SLD})</math> | ||
| + | |- | ||
| + | | <math>\sigma = \frac{M_a}{\rho N_a \epsilon} </math> | ||
| + | | <math>\sigma = \frac{M_a}{\rho N_a} \mu</math> | ||
| + | | <math>\sigma = \frac{M_a}{N_a} \frac{\mu}{\rho}</math> | ||
| + | | <math>\sigma = 2 r_e \lambda f_2</math> | ||
| + | | <math>\sigma</math> | ||
| + | | <math>\sigma = \frac{4 \pi M_a}{ \rho N_a \lambda } \beta</math> | ||
| + | | <math>\sigma = \frac{2 \lambda M_a}{\rho N_a}\mathrm{Im}(\mathrm{SLD})</math> | ||
| + | |- | ||
| + | | <math>\beta = \frac{ \lambda }{4 \pi \epsilon}</math> | ||
| + | | <math>\beta = \frac{ \lambda }{4 \pi } \mu</math> | ||
| + | | <math>\beta = \frac{ \rho \lambda }{4 \pi } \frac{\mu}{\rho}</math> | ||
| + | | <math>\beta = \frac{ \rho N_a r_e \lambda^2 }{2 \pi M_a} f_2</math> | ||
| + | | <math>\beta = \frac{ \rho N_a \lambda }{4 \pi M_a} \sigma</math> | ||
| + | | <math>\beta</math> | ||
| + | | <math>\beta = \frac{\lambda^2}{2 \pi} \mathrm{Im}(\mathrm{SLD})</math> | ||
| + | |- | ||
| + | | <math>\mathrm{Im}(\mathrm{SLD}) = \frac{1 }{2 \lambda \epsilon} </math> | ||
| + | | <math>\mathrm{Im}(\mathrm{SLD}) = \frac{\mu}{2 \lambda} </math> | ||
| + | | <math>\mathrm{Im}(\mathrm{SLD}) = \frac{\rho }{2 \lambda} \frac{\mu}{\rho}</math> | ||
| + | | <math>\mathrm{Im}(\mathrm{SLD}) = \frac{\rho N_a r_e }{M_a} f_2</math> | ||
| + | | <math>\mathrm{Im}(\mathrm{SLD}) = \frac{\rho N_a}{2 \lambda M_a}\sigma</math> | ||
| + | | <math>\mathrm{Im}(\mathrm{SLD}) = \frac{2 \pi }{\lambda^2} \beta</math> | ||
| + | | <math>\mathrm{Im}(\mathrm{SLD})</math> | ||
| + | |||
| + | |} | ||
| + | |||
| + | |||
| + | See also '''[[Atomic_scattering_factors#Related_forms|scattering factors]]''' for a comparison of the quantities related to ''f''<sub>1</sub>. | ||
==See Also== | ==See Also== | ||
| + | * [[Resonant scattering]] | ||
| + | ** [[RSoXS]] | ||
| + | ** [[Resonant reflectivity]] | ||
* [http://henke.lbl.gov/optical_constants/atten2.html LBL X-Ray Attenuation Length calculator] | * [http://henke.lbl.gov/optical_constants/atten2.html LBL X-Ray Attenuation Length calculator] | ||
| − | * [http://11bm.xray.aps.anl.gov/absorb/absorb.php APS absorption calculator | + | * [http://11bm.xray.aps.anl.gov/absorb/absorb.php APS absorption calculator] |
| + | * [http://henke.lbl.gov/optical_constants/filter2.html CXRO transmission calculator] | ||
* [http://en.wikipedia.org/wiki/Mass_attenuation_coefficient Wikipedia: Mass attenuation coefficient] | * [http://en.wikipedia.org/wiki/Mass_attenuation_coefficient Wikipedia: Mass attenuation coefficient] | ||
| + | * [http://en.wikipedia.org/wiki/Absorption_cross_section Wikipedia: Absorption cross sectio] | ||
* [http://www.nist.gov/pml/data/xraycoef/ NIST tables of x-ray mass attenuation coefficient] | * [http://www.nist.gov/pml/data/xraycoef/ NIST tables of x-ray mass attenuation coefficient] | ||
Latest revision as of 15:43, 29 July 2015
The absorption length or attenuation length in x-ray scattering is the distance over which the x-ray beam is absorbed. By convention, the absorption length ϵ is defined as the distance into a material where the beam flux has dropped to 1/e of its incident flux.
Contents
Absorption
The absorption follows a simple Beer-Lambert law:
The attenuation coefficient (or absorption coefficient) is simply the inverse of the absorption length;
Calculating
The absorption length arises from the imaginary part of the atomic scattering factor, f2. It is closely related to the absorption cross-section, and the mass absorption coefficient. Specifically, the atomic photoabsorption cross-section can be computed via:
Where λ is the x-ray wavelength, and re is the classical electron radius. The attenuation coefficient is given by:
where ρ is density, Na is the Avogadro constant, and ma is the atomic molar mass. Note that the mass attenuation coefficient is simply .
Elemental dependence
Energy dependence
Notice that the absorption undergoes sharp increases when passing through an absorption edge.
Examples
silicon
gold
Elemental/Energy dependence
Related forms
As can be seen, there are many related quantities which express the material's absorption:
- Absorption length , the distance over which the intensity falls to 1/e.
- Attenuation coefficient , the characteristic inverse-distance for attenuation.
- Mass attenuation coefficient , the density-scaled attenuation.
- Absorptive atomic scattering factor , the intrinsic dissipative interaction of the material.
- Atomic photoabsorption cross-section , the cross-section ('effective size') of the atom's x-ray absorption (capture) efficiency.
- Imaginary refractive index , the resonant component of the refractive index.
- Imaginary Scattering Length Density , the absorptive component of the scattering contrast.
See also scattering factors for a comparison of the quantities related to f1.