Difference between revisions of "Refraction distortion"

Revision as of 13:41, 4 November 2015

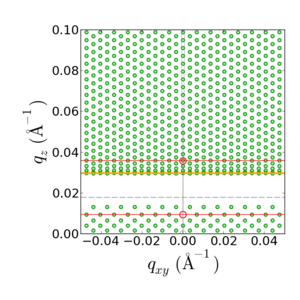
Illustration of GISAXS refraction distortion. The reciprocal-space scattering is a hexagonal array of peaks. However, these peaks are both shifted, and compressed/stretched along q_z, due to refraction. This effect is especially pronounced near the Yoneda (orange line).

In GISAXS, GIWAXS, and other grazing-incidence techniques, the refractive index difference between the film and the ambient causes the incident and scattered x-ray beams to be refracted. This extent of refraction depends on the incident and exit angles. Thus, the data that appears on an area detector in a grazing-incidence experiment is non-linearly distorted. This makes data interpretation more problematic.

Mathematics

The GISAXS refraction distortion shifts the data along $\scriptstyle q_{z}$ , leaving $\scriptstyle q_{x}$ unaffected. The amount of the shift is given by:

{\begin{alignedat}{2}\Delta q_{z}&=q_{z}-q_{z}^{\prime }\\q'_{z}&=k_{0}\left({\sqrt {\sin \alpha _{i}^{2}-\sin \alpha _{ct}^{2}}}+{\sqrt {\sin \alpha _{f}^{2}-\sin \alpha _{ct}^{2}}}\right)\\&=k_{0}\left({\sqrt {\sin \alpha _{i}^{2}-\sin \alpha _{ct}^{2}}}+{\sqrt {\left({\frac {q_{z}}{k_{0}}}-\sin \alpha _{i}\right)^{2}-\sin \alpha _{ct}^{2}}}\right)\end{alignedat}}

Where $\scriptstyle \alpha _{i}$ is the incident angle, and $\scriptstyle \alpha _{ct}$ is the critical angle of the film.

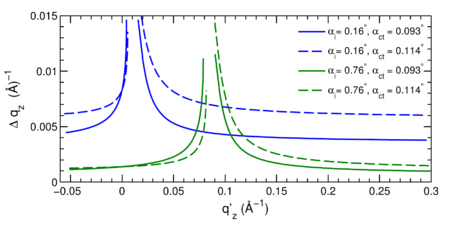
Figure from Lu. et al. (doi: 10.1107/S0021889812047887 J. of Appl. Cryst. 2013, 46, 165) showing the amount of distortion along q_z, for different conditions.

Refraction Correction

When computing theoretical scattering patterns, one must account for the refraction correction. The correction is essentially an application of Snell's law, where one using the x-ray refractive index for ambient ( $\scriptstyle n_{a}$ ), the thin film ( $\scriptstyle n_{f}$ ), and the substrate ( $\scriptstyle n_{s}$ ). For an incident angle of $\scriptstyle \alpha _{i}$ , one computes a refraction of:

\alpha _{ie}=\cos ^{-1}\left({\frac {n_{a}}{n_{f}}}\cos(\alpha _{i})\right)

That is, the direct beam shifts by $\scriptstyle \alpha _{i}-\alpha _{ie}$ . For a given $\scriptstyle q_{z}$ , one can convert into scattering angle:

2\theta _{B}=2\sin ^{-1}\left({\frac {q_{z}}{2k}}\right)

The scattered ray refracts as it exits from the film:

{\begin{alignedat}{2}\alpha _{s}&=2\theta _{B}-\alpha _{ie}\\\alpha _{e}&=\cos ^{-1}\left({\frac {n_{f}}{n_{a}}}\cos(\alpha _{s})\right)\end{alignedat}}

If $\scriptstyle \alpha _{e}>0$ , then scattering is above the horizon (GISAXS); if $\scriptstyle \alpha _{e}<0$ , then it is sub-horizon scattering (GTSAXS). For GISAXS, the final scattering angle is: