Difference between revisions of "Refraction distortion"
KevinYager (talk | contribs) |
KevinYager (talk | contribs) (→Refraction Correction) |
||
| (7 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
==Mathematics== | ==Mathematics== | ||
The GISAXS refraction distortion shifts the data along <math>\scriptstyle q_z</math>, leaving <math>\scriptstyle q_x</math> unaffected. The amount of the shift is given by: | The GISAXS refraction distortion shifts the data along <math>\scriptstyle q_z</math>, leaving <math>\scriptstyle q_x</math> unaffected. The amount of the shift is given by: | ||
| + | :<math> | ||
| + | \begin{alignat}{2} | ||
| + | \Delta q_z & = q_z - q_z^{\prime} \\ | ||
| + | q'_z & = k_0\left(\sqrt{\sin\alpha_i^2 - \sin\alpha_{ct}^2} + \sqrt{\sin\alpha_f^2 - \sin\alpha_{ct}^2}\right) \\ | ||
| + | & = k_0\left(\sqrt{\sin\alpha_i^2 - \sin\alpha_{ct}^2} + \sqrt{\left(\frac{q_z}{k_0} - \sin\alpha_i\right)^2 - \sin\alpha_{ct}^2}\right) | ||
| − | [[Image:Lu GTSAXS-Figure5.png|center|thumb| | + | \end{alignat} |
| + | </math> | ||
| + | Where <math>\scriptstyle \alpha_i</math> is the incident angle, and <math>\scriptstyle \alpha_{ct}</math> is the [[critical angle]] of the film. | ||
| + | |||
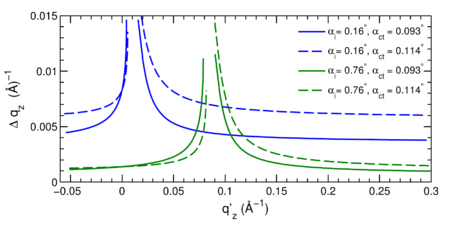
| + | [[Image:Lu GTSAXS-Figure5.png|center|thumb|450px|Figure from Lu. et al. ([http://dx.doi.org/10.1107/S0021889812047887 doi: 10.1107/S0021889812047887 ''J. of Appl. Cryst.'' '''2013''', 46, 165]) showing the amount of distortion along ''q<sub>z</sub>'', for different conditions.]] | ||
==Refraction Correction== | ==Refraction Correction== | ||
| − | When computing theoretical scattering patterns, one must account for the refraction correction. | + | When computing theoretical scattering patterns, one must account for the refraction correction. The correction is essentially an application of Snell's law, where one using the x-ray [[refractive index]] for ambient (<math>\scriptstyle n_a</math>), the thin film (<math>\scriptstyle n_f</math>), and the substrate (<math>\scriptstyle n_s</math>). For an incident angle of <math>\scriptstyle \alpha_i</math>, one computes a refraction of: |
| + | :<math> | ||
| + | \alpha_{ie} = \cos^{-1} \left( \frac{n_a}{n_f}\cos(\alpha_i) \right ) | ||
| + | </math> | ||
| + | That is, the direct beam shifts by <math>\scriptstyle \alpha_i - \alpha_{ie}</math>. For a given <math>\scriptstyle q_z</math>, one can convert into scattering angle: | ||
| + | :<math> | ||
| + | 2\theta_B = 2 \sin^{-1} \left( \frac{q_z}{2 k} \right) | ||
| + | </math> | ||
| + | The scattered ray refracts as it exits from the film: | ||
| + | :<math> | ||
| + | \begin{alignat}{2} | ||
| + | \alpha_{s} & = 2\theta_B - \alpha_{ie} \\ | ||
| + | \alpha_{e} & = \cos^{-1} \left( \frac{n_f}{n_a}\cos(\alpha_s) \right) | ||
| + | \end{alignat} | ||
| + | </math> | ||
| + | If <math>\scriptstyle \alpha_e>0</math>, then scattering is above the [[horizon]] ([[GISAXS]]); if <math>\scriptstyle \alpha_e<0</math>, then it is sub-horizon scattering ([[GTSAXS]]). For GISAXS, the final scattering angle is: | ||
| + | :<math> | ||
| + | \begin{alignat}{2} | ||
| + | \Delta \alpha_s & = \alpha_e-\alpha_s \\ | ||
| + | 2\theta_{Bf} & = \alpha_i + \alpha_e \\ | ||
| + | q_z\prime & = 2 k \sin( 2 \theta_B /2 ) | ||
| + | \end{alignat} | ||
| + | </math> | ||
| + | |||
* Byeongdu Lee, Insun Park, Jinhwan Yoon, Soojin Park, Jehan Kim, Kwang-Woo Kim, Taihyun Chang, and Moonhor Ree [http://pubs.acs.org/doi/abs/10.1021/ma047562d Structural Analysis of Block Copolymer Thin Films with Grazing Incidence Small-Angle X-ray Scattering] ''Macromolecules'' '''2005''', 38 (10), 4311-4323. [http://dx.doi.org/10.1021/ma047562d doi: 10.1021/ma047562d] | * Byeongdu Lee, Insun Park, Jinhwan Yoon, Soojin Park, Jehan Kim, Kwang-Woo Kim, Taihyun Chang, and Moonhor Ree [http://pubs.acs.org/doi/abs/10.1021/ma047562d Structural Analysis of Block Copolymer Thin Films with Grazing Incidence Small-Angle X-ray Scattering] ''Macromolecules'' '''2005''', 38 (10), 4311-4323. [http://dx.doi.org/10.1021/ma047562d doi: 10.1021/ma047562d] | ||
| Line 16: | Line 48: | ||
* D. W. Breiby, O. Bunk, J. W. Andreasen, H. T. Lemke and M. M. Nielsen [http://scripts.iucr.org/cgi-bin/paper?S0021889808001064 Simulating X-ray diffraction of textured films] ''J. Appl. Cryst.'' 2008, 41, 262-271. [http://dx.doi.org/10.1107/S0021889808001064 doi: 10.1107/S0021889808001064] | * D. W. Breiby, O. Bunk, J. W. Andreasen, H. T. Lemke and M. M. Nielsen [http://scripts.iucr.org/cgi-bin/paper?S0021889808001064 Simulating X-ray diffraction of textured films] ''J. Appl. Cryst.'' 2008, 41, 262-271. [http://dx.doi.org/10.1107/S0021889808001064 doi: 10.1107/S0021889808001064] | ||
* Lu, X.; [[Yager, K.G.]]; Johnston, D.; Black, C.T.; Ocko, B.M. '''[http://scripts.iucr.org/cgi-bin/paper?S0021889812047887 Grazing-incidence transmission X-ray scattering: surface scattering in the Born approximation]''' ''Journal of Applied Crystallography'' '''2013''', 46, 165–172. [http://dx.doi.org/10.1107/S0021889812047887 doi: 10.1107/S0021889812047887] | * Lu, X.; [[Yager, K.G.]]; Johnston, D.; Black, C.T.; Ocko, B.M. '''[http://scripts.iucr.org/cgi-bin/paper?S0021889812047887 Grazing-incidence transmission X-ray scattering: surface scattering in the Born approximation]''' ''Journal of Applied Crystallography'' '''2013''', 46, 165–172. [http://dx.doi.org/10.1107/S0021889812047887 doi: 10.1107/S0021889812047887] | ||
| + | * Liu, J.; Yager, K.G. [http://journals.iucr.org/m/issues/2018/06/00/hf5364/index.html Unwarping GISAXS data] ''IUCrJ'' '''2018''', 5, 737–752. [http://dx.doi.org/10.1107/S2052252518012058 doi: 10.1107/S2052252518012058] | ||
==See Also== | ==See Also== | ||
Latest revision as of 07:49, 16 April 2019
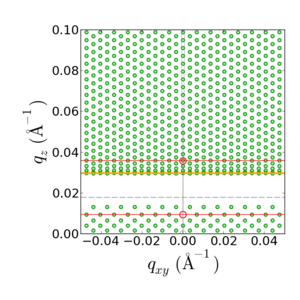
In GISAXS, GIWAXS, and other grazing-incidence techniques, the refractive index difference between the film and the ambient causes the incident and scattered x-ray beams to be refracted. This extent of refraction depends on the incident and exit angles. Thus, the data that appears on an area detector in a grazing-incidence experiment is non-linearly distorted. This makes data interpretation more problematic.
Mathematics
The GISAXS refraction distortion shifts the data along , leaving unaffected. The amount of the shift is given by:
Where is the incident angle, and is the critical angle of the film.
Refraction Correction
When computing theoretical scattering patterns, one must account for the refraction correction. The correction is essentially an application of Snell's law, where one using the x-ray refractive index for ambient (), the thin film (), and the substrate (). For an incident angle of , one computes a refraction of:
That is, the direct beam shifts by . For a given , one can convert into scattering angle:
The scattered ray refracts as it exits from the film:
If , then scattering is above the horizon (GISAXS); if , then it is sub-horizon scattering (GTSAXS). For GISAXS, the final scattering angle is:
- Byeongdu Lee, Insun Park, Jinhwan Yoon, Soojin Park, Jehan Kim, Kwang-Woo Kim, Taihyun Chang, and Moonhor Ree Structural Analysis of Block Copolymer Thin Films with Grazing Incidence Small-Angle X-ray Scattering Macromolecules 2005, 38 (10), 4311-4323. doi: 10.1021/ma047562d
- P. Busch, M. Rauscher, D.-M. Smilgies, D. Posselt and C. M. Papadakis Grazing-incidence small-angle X-ray scattering from thin polymer films with lamellar structures - the scattering cross section in the distorted-wave Born approximation J. Appl. Cryst. 2006, 39, 433-442. doi: 10.1107/S0021889806012337
- Rémi Lazzari, Frédéric Leroy, and Gilles Renaud Grazing-incidence small-angle x-ray scattering from dense packing of islands on surfaces: Development of distorted wave Born approximation and correlation between particle sizes and spacing Phys. Rev. B 2007, 76, 125411. doi: 10.1103/PhysRevB.76.125411
- D. W. Breiby, O. Bunk, J. W. Andreasen, H. T. Lemke and M. M. Nielsen Simulating X-ray diffraction of textured films J. Appl. Cryst. 2008, 41, 262-271. doi: 10.1107/S0021889808001064
- Lu, X.; Yager, K.G.; Johnston, D.; Black, C.T.; Ocko, B.M. Grazing-incidence transmission X-ray scattering: surface scattering in the Born approximation Journal of Applied Crystallography 2013, 46, 165–172. doi: 10.1107/S0021889812047887
- Liu, J.; Yager, K.G. Unwarping GISAXS data IUCrJ 2018, 5, 737–752. doi: 10.1107/S2052252518012058
See Also
- DWBA
- Simulating X-ray diffraction of textured films D. W. Breiby, O. Bunk, J. W. Andreasen, H. T. Lemke and M. M. Nielsen J. Appl. Cryst. 2008, 41, 262-271. doi: 10.1107/S0021889808001064
- Indexation scheme for oriented molecular thin films studied with grazing-incidence reciprocal-space mapping D.-M. Smilgies and D. R. Blasini J. Appl. Cryst. 2007, 40, 716-718. doi: 10.1107/S0021889807023382
- Grazing-incidence small-angle X-ray scattering from thin polymer films with lamellar structures - the scattering cross section in the distorted-wave Born approximation P. Busch, M. Rauscher, D.-M. Smilgies, D. Posselt and C. M. Papadakis J. Appl. Cryst. 2006, 39, 433-442. doi: 10.1107/S0021889806012337














