Difference between revisions of "Refractive index"
(Created page with "The '''refractive index''' for x-rays is strictly analogous to the conventional (visible light) refractive index: it describes how strongly wave propagation is altered within ...") |
KevinYager (talk | contribs) (→See Also) |
||
| (18 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | The '''refractive index''' for x-rays is strictly analogous to the conventional (visible light) refractive index | + | The '''refractive index''' for [[x-rays]] is strictly analogous to the conventional (visible light) refractive index. It describes how strongly wave propagation is altered within the given material. The modification of the wave's phase velocity in turn causes the propagation direction to be altered (i.e. the wave is refracted). |
==Total external reflection== | ==Total external reflection== | ||
X-rays interact rather weakly with matter (e.g. [[absorption lengths]] are on the order of millimeters); x-ray refractive indices are thus extremely close to 1. In fact, x-ray refractive indices tend to be slightly ''smaller'' than 1, giving rise to total ''external'' reflection at sufficiently small angle. This can be compared to total ''internal'' reflection typically observed for visible light. | X-rays interact rather weakly with matter (e.g. [[absorption lengths]] are on the order of millimeters); x-ray refractive indices are thus extremely close to 1. In fact, x-ray refractive indices tend to be slightly ''smaller'' than 1, giving rise to total ''external'' reflection at sufficiently small angle. This can be compared to total ''internal'' reflection typically observed for visible light. | ||
| − | Visible light can be totally reflected when travelling from a denser medium into a less denser medium (e.g. light traveling in glass towards a glass-air interface will be totally reflected when the incident angle (measured from the interface) is less than ~50°). Whereas for x-rays, the beam can be totally reflected when travelling from a less dense medium into a denser medium (e.g. x-rays traveling in vacuum towards a | + | Visible light can be totally reflected when travelling from a denser medium into a less denser medium (e.g. light traveling in glass towards a glass-air interface will be totally reflected when the incident angle (measured from the interface) is less than ~50°). Whereas for x-rays, the beam can be totally reflected when travelling from a less dense medium into a denser medium (e.g. x-rays traveling in vacuum towards a [[Material:Vacuum|vacuum]]-[[Material:Silicon|silicon]] interface will be totally reflected if the grazing-incidence angle is less than ~0.2°). |
| − | Notice that because the refractive index is very close to 1, the critical | + | Notice that because the refractive index is very close to 1, the [[critical angle]]s are very small (as measured from the interface). The critical angle depends on the x-ray energy and the material, but is typically on the order of 0.1° to 0.5°. |
==Mathematical form== | ==Mathematical form== | ||
| Line 13: | Line 13: | ||
n = 1 - \delta + i \beta | n = 1 - \delta + i \beta | ||
</math> | </math> | ||
| − | The real and imaginary components, | + | The real and imaginary components, <math>\scriptstyle \delta </math> and ''β'', describe the dispersive and absorptive aspects of the wave-matter interaction. These components can be calculated from the [[atomic scattering factors]] (''f''<sub>1</sub> and ''f''<sub>2</sub>) using: |
:<math> | :<math> | ||
\delta = \frac{ n_a r_e \lambda^2 }{2 \pi} f_1 | \delta = \frac{ n_a r_e \lambda^2 }{2 \pi} f_1 | ||
| Line 24: | Line 24: | ||
n_a = \frac{\rho N_a}{M_a} | n_a = \frac{\rho N_a}{M_a} | ||
</math> | </math> | ||
| − | where ''ρ'' is the physical density (e.g. in g/cm<sup>3</sup>), ''N<sub>a</sub>'' is the [http://en.wikipedia.org/wiki/Avogadro_constant Avogadro constant] (6.02214129x10<sup>23</sup> mol<sup>−1</sup>), and ''M<sub>a</sub>'' is molar mass (e.g. in g/mol). There are also [http://henke.lbl.gov/optical_constants/getdb2.html online tools] that will compute the refractive index for you. | + | where ''ρ'' is the physical density (e.g. in g/cm<sup>3</sup>), ''N<sub>a</sub>'' is the [http://en.wikipedia.org/wiki/Avogadro_constant Avogadro constant] (6.02214129x10<sup>23</sup> mol<sup>−1</sup>), and ''M<sub>a</sub>'' is molar mass (e.g. in g/mol). There are also [http://henke.lbl.gov/optical_constants/getdb2.html online tools] that will compute the refractive index for you. The real part of the refractive index can also be directly related to the [[electron-density distribution|electron-density]]: |
| + | :<math> | ||
| + | \begin{alignat}{2} | ||
| + | \rho_e & = \frac{\rho N_a f_1}{M_a} \\ | ||
| + | & = \frac{2 \pi}{\lambda^2 r_e} \delta | ||
| + | \end{alignat} | ||
| + | </math> | ||
==Refraction== | ==Refraction== | ||
The refraction of x-rays follows the same laws as for refraction of visible light. I.e. [http://en.wikipedia.org/wiki/Snell%27s_law snell's law]. However, in [[GISAXS]] and [[reflectivity]], we conventionally describe the incident angle with respect to the plane of the interface (rather than being measured with respect to the film normal, as done in visible light optics). As such, the sine version of snell's law is converted into a cosine version: | The refraction of x-rays follows the same laws as for refraction of visible light. I.e. [http://en.wikipedia.org/wiki/Snell%27s_law snell's law]. However, in [[GISAXS]] and [[reflectivity]], we conventionally describe the incident angle with respect to the plane of the interface (rather than being measured with respect to the film normal, as done in visible light optics). As such, the sine version of snell's law is converted into a cosine version: | ||
:<math> | :<math> | ||
| − | \frac{\theta_1}{\theta_2} = \frac{n_2}{n_1} | + | \frac{\cos \theta_1}{\cos \theta_2} = \frac{n_2}{n_1} |
</math> | </math> | ||
| + | |||
| + | ==Elemental dependence== | ||
| + | |||
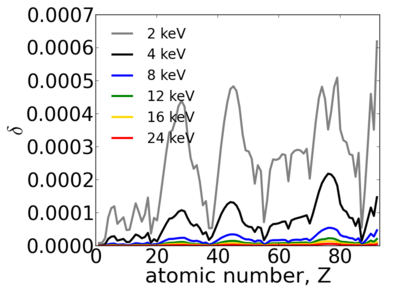
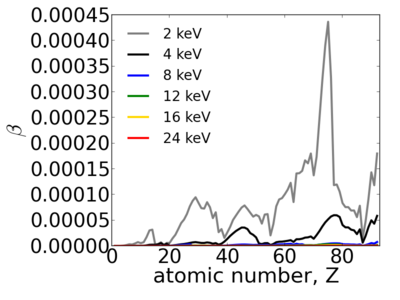
| + | [[Image:Elements-delta.png|400px]][[Image:Elements-beta.png|400px]] | ||
| + | |||
| + | ==Energy dependence== | ||
| + | The ''λ''<sup>2</sup> term causes the refractive index to decrease rapidly with increasing x-ray energy. In other words, high-energy (short wavelength) x-rays are relatively unaffected by their propagation through matter. | ||
| + | |||
| + | ===Examples=== | ||
| + | |||
| + | ====[[Material:Silicon|silicon]]==== | ||
| + | |||
| + | [[Image:Silicon-n.png|400px]] | ||
| + | |||
| + | ====[[Material:Gold|gold]]==== | ||
| + | |||
| + | [[Image:Gold-n.png|400px]] | ||
| + | |||
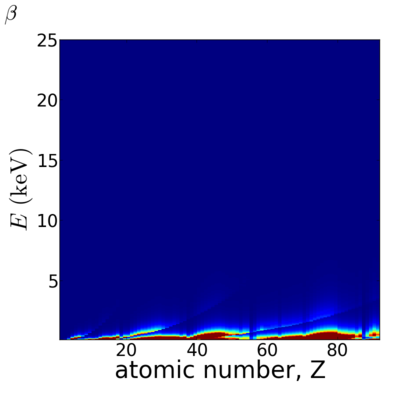
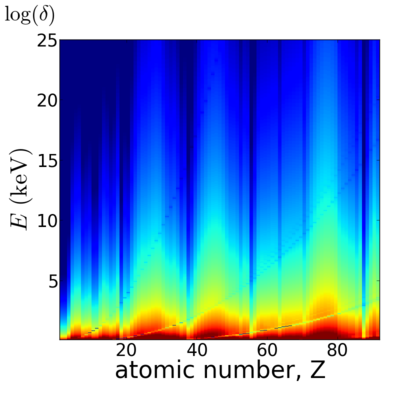
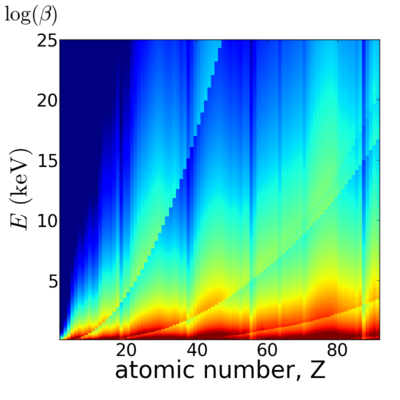
| + | ==Elemental/Energy dependence== | ||
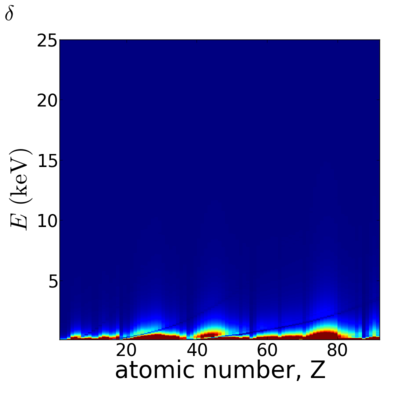
| + | [[Image:Elements2D-delta.png|400px]][[Image:Elements2D-beta.png|400px]] | ||
| + | |||
| + | [[Image:Elements2D-logdelta.png|400px]][[Image:Elements2D-logbeta.png|400px]] | ||
| + | |||
| + | ==See Also== | ||
| + | * [[Critical angle]] | ||
| + | * [[Scattering Length Density]] | ||
| + | * [http://henke.lbl.gov/optical_constants/getdb2.html CXRO refractive index calculator] | ||
| + | * Liu, J.; Yager, K.G. [http://journals.iucr.org/m/issues/2018/06/00/hf5364/index.html Unwarping GISAXS data] ''IUCrJ'' '''2018''', 5, 737–752. [http://dx.doi.org/10.1107/S2052252518012058 doi: 10.1107/S2052252518012058] | ||
Latest revision as of 07:49, 16 April 2019
The refractive index for x-rays is strictly analogous to the conventional (visible light) refractive index. It describes how strongly wave propagation is altered within the given material. The modification of the wave's phase velocity in turn causes the propagation direction to be altered (i.e. the wave is refracted).
Contents
Total external reflection
X-rays interact rather weakly with matter (e.g. absorption lengths are on the order of millimeters); x-ray refractive indices are thus extremely close to 1. In fact, x-ray refractive indices tend to be slightly smaller than 1, giving rise to total external reflection at sufficiently small angle. This can be compared to total internal reflection typically observed for visible light.
Visible light can be totally reflected when travelling from a denser medium into a less denser medium (e.g. light traveling in glass towards a glass-air interface will be totally reflected when the incident angle (measured from the interface) is less than ~50°). Whereas for x-rays, the beam can be totally reflected when travelling from a less dense medium into a denser medium (e.g. x-rays traveling in vacuum towards a vacuum-silicon interface will be totally reflected if the grazing-incidence angle is less than ~0.2°).
Notice that because the refractive index is very close to 1, the critical angles are very small (as measured from the interface). The critical angle depends on the x-ray energy and the material, but is typically on the order of 0.1° to 0.5°.
Mathematical form
The complex refractive index is customarily denoted as:
The real and imaginary components, and β, describe the dispersive and absorptive aspects of the wave-matter interaction. These components can be calculated from the atomic scattering factors (f1 and f2) using:
Where re is the classical electron radius (2.8179403x10−15 m), λ is the wavelength of the probing x-rays, and na is the number density:
where ρ is the physical density (e.g. in g/cm3), Na is the Avogadro constant (6.02214129x1023 mol−1), and Ma is molar mass (e.g. in g/mol). There are also online tools that will compute the refractive index for you. The real part of the refractive index can also be directly related to the electron-density:
Refraction
The refraction of x-rays follows the same laws as for refraction of visible light. I.e. snell's law. However, in GISAXS and reflectivity, we conventionally describe the incident angle with respect to the plane of the interface (rather than being measured with respect to the film normal, as done in visible light optics). As such, the sine version of snell's law is converted into a cosine version:
Elemental dependence
Energy dependence
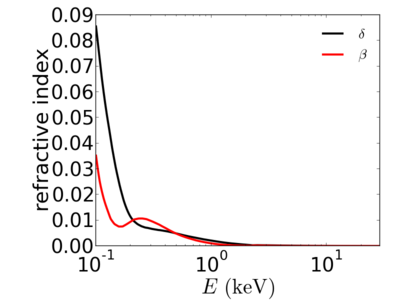
The λ2 term causes the refractive index to decrease rapidly with increasing x-ray energy. In other words, high-energy (short wavelength) x-rays are relatively unaffected by their propagation through matter.
Examples
silicon
gold
Elemental/Energy dependence
See Also
- Critical angle
- Scattering Length Density
- CXRO refractive index calculator
- Liu, J.; Yager, K.G. Unwarping GISAXS data IUCrJ 2018, 5, 737–752. doi: 10.1107/S2052252518012058