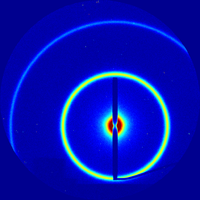
Tutorial:Qualitative inspection
When analyzing data, the first thing one should do is get an overall sense of data. By applying a few simple rules-of-thumb, one can interpret a 2D x-ray scattering image, understanding the origin of various features, and infer quite a bit about the structure of the sample.
Contents
Amount of Order
One can roughly estimate the 'amount of order' by simply inspecting the scattering data.
No Scattering
A lack of scattering signal is a good indicator that the sample lacks any kind of well-defined structure (at least in the size-scales being probed by the available q-range). Of course, one must be careful to eliminate other possibilities: sample misaligned, beam flux too low, etc. A particular pathological possibility is that the sample is actually extremely well-ordered (e.g. single crystal), but just happens to be in an alignment where none of the reciprocal-space peaks are on the detector. (If you suspect this is the case, you should try reorienting the sample.)
Diffuse Scattering
Diffuse scattering is the scattering intensity which is spread over a wide range of q-values, and lacks any definite structure (i.e. it is not concentrated into a peak, ring, or even broad halo). This kind of scattering arises from structuring that is not periodic or otherwise well-ordered. Thus, it arises from random ordering, or from disorder. For instance, a nanoporous material (sponge-like, with voids of many different sizes) will give rise to intense low-q diffuse scattering. A rough surface will create substantial diffuse scattering (a broad and bright specular rod) in GISAXS. Thus, diffuse scattering is a signature of some kind of random realspace structure. Unfortunately, quantitative analysis of this kind of scattering is quite difficult (since there are so many models that give rise to essentially the same diffuse scattering signature).
Single Broad Ring (Halo)
A sharp scattering ring arises from a well-defined repeating structure (that is otherwise oriented isotropically). A broad ring typically arises from a structure that has some level of local order, but where this order does not persist over large distances. For instance, random nanoparticle packing will likely have a preferred particle-particle distance, giving rise to a halo in SAXS. The lack of long-range order makes the halo broad. Similarly, amorphous or semi-crystalline polymers frequently exhibit a halo in the wide-angle, arising from the preferred chain packing distance.
Single Ring
The appearance of a single (relatively sharp) scattering ring indicates that the material exhibits a well-defined periodic ordering in realspace. The peak width can be used to estimate the distance over which this order is maintained (i.e. the grain size). A smooth ring (equal intensity at all angles) indicates that the sample is isotropic (grains in every possible orientation).
Multiple Rings
The appearance of multiple scattering rings indicates a well-ordered material. The various rings arise from different crystallographic planes in the unit cell, which again point to a very well-defined local packing, which is then repeated throughout space.
Multiple Sharp Rings
Scattering that involves many sharp rings indicates a highly-ordered system: for WAXS, this usually means a crystal; for SAXS, this similarly means a nanoscale crystal-like ordering, such as a superlattice.
Speckled Rings
Scattering rings are isotropic when the beam probes a distribution of grains at every possible orientation. If the grains become sufficiently large, the beam no longer probes a uniform distribution; instead it probes a random sampling of grains at specific orientations. The result is that the ring becomes 'speckled' or 'grainy' (this can be quantified to estimate grain size). Thus, highly speckled rings indicate crystalline order that is 'extremely good'.
Multiple Sharp Peaks
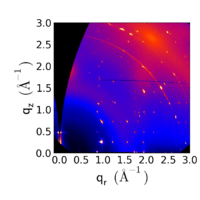
When scattering patterns exhibit distinct peaks, rather than rings, this indicates that the material is well-ordered, and well-oriented. Thus, the sample's structure is not isotropic: there is a preferred orientation for the material.
Peak Position
The position of a peak in GISAXS allows one to infer the sizescale of the realspace ordering. Recall that reciprocal-space is inverted: i.e. peaks at large angle (large q) correspond to small-scale structures; whereas peaks at small angle (small q) correspond to larger (nanoscale) structures. Ultrasmall angle scattering (USAXS) probes yet larger (micron-scale) order. More specifically, when observing peaks at:
- Very large angle (0.5-4 Å−1): Atomic packing distances (1-10 Å).
- Large angle (0.2-2 Å−1): Molecular packing distances (0.3-3 nm). For instance, aromatic rings tend to pi-pi stack with a 0.3-0.4 nm repeat distance.
- Medium angle (0.03-0.3 Å−1): Macromolecular distances (2-20 nm). For instance, polymers often crystallize into chain-folded lamellae with a period of 2-10 nm.
- Small angle (0.0002-0.04 Å−1): Nanoscale distances (15-300 nm). For instance, block-copolymers and nanoparticle superlattices tend to organize in this size regime.
- Ultra-small angle (<0.0006 Å−1): Micron sizes (>1 µm).
Peak Width
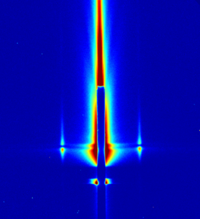
In scattering, sharp peaks correspond to large grain sizes, whereas broad peaks correspond to small grain sizes. This can be quantified through a Scherrer grain size analysis. Even qualitatively, however, it is usually easy to judge how well-ordered a material is based purely on peak widths. Consider a highly disordered system, such as an amorphous polymer. The polymer chains likely have some preferred chain-packing distance, but the 'lattice' only repeats once or twice before decorrelating; i.e. there isn't a well-defined crystal with well defined grain boundaries. In such a case one would see a very broad halo. In even more disordered systems, only diffuse scattering would be seen (this can be thought of as the ultimate limit of a broad peak).
On the other hand, extremely sharp peaks indicate that the lattice repeats in a well-correlated way over very large distances. Thus, sharp peaks arise when one has well-defined crystals.
Scattering Intensity
The total scattering intensity one observes on the detector is affected by a number of factors. The scattering intensity of course influences the time required for taking a measurement.
Flux
Obviously, the observed scattering intensity is depending on beam flux. A high-flux beam will yield a correspondingly higher number of counts/second than a lower-flux beam. So, when comparing scattering intensities, one must account for the beam flux, and the measurement time.
Scattering Volume
The scattering intensity (counts on the x-ray detector per unit time) scales with the amount of scattering material. Thus, a bigger sample yields a stronger scattering signal. The truly relevant quantity is the scattering volume: the intersection between the x-ray beam and the sample. (Of course if you try to scatter through a sample that is too thick, absorption or multiple scattering will at some point instead reduce the signal.) In GISAXS, the scattering volume can be difficult to estimate accurately: one must account for the beam width, the sample thickness, and the beam projection along the beam direction (while accounting for whether this projected beam size or the sample dimensions limits the scattering volume in this direction).
Note that because real x-ray beams are not not square-waves (i.e. they have a pseudo-Gaussian cross section), and scattering intensity is affected by flux, determining the relevant scattering volume can be subtle (c.f. integral breadth).
Amount of Material
For a given scattering volume, the intensity of the scattering can be thought of as a probe of the fraction of the material in the given state/phase/configuration. I.e. if a given peak is stronger in one sample vs. another, then this means that the phase (crystal form, etc.) corresponding to that peak appears more frequently in that sample. One must be careful, however, as many other things are implicated in peak heights (orientation, disorder, etc.).
Order
Note that in general, well-ordered systems will appear to scatter more strongly than weakly-ordered systems. A broad scattering peak (small grains) will have lower maximum intensity than a sharp scattering peak (big grains). More generally, periodically ordered structures give rise to scattering events, whereas homogeneous systems do not scattering the incident radiation.
Scattering Contrast
The intensity of scattering scales with the square of the scattering contrast. For x-rays, scattering arises from electron density; i.e. the relevant contrast is the electron-density difference between the two phases. (For neutrons scattering, the nuclear Scattering Length Density is the relevant contrast.) For instance, gold spheres sitting in vacuum will have extremely large contrast and will lead to very intense scattering. Equivalently-sized polystyrene spheres sitting in water will have much lower scattering contrast. Many soft-matter systems thus have weak contrast: e.g. block-copolymer mesophases involve two different polymer species, with nearly identical densities. Thus their scattering contrast is comparatively weak (but can still be probed using synchrotron beamlines).
Scattering contrast can be intentionally varied in order to gain additional information about a system. For instance, one can measure a porous system in air, and then with solvent filling the pores. The difference in scattering allows one to assess the structure. For multi-component systems, one can intentionally 'contrast-match' a particular species, making it invisible (to scattering).
Higher Orders
Higher-order peaks in x-ray scattering generally imply a well-defined structure. Qualitatively, if you see lots of higher-orders, you can say you have a very well-organized structure. For molecular peaks, this usually means a high-quality crystal (with large grain sizes). For nanoscale peaks, this usually means a well-defined superlattice of some kind.
Conversely, disorder tends to broaden peaks, and also extinguish the intensity of higher-order peaks (c.f. Debye-Waller factor). Observing only a single peak means a highly disordered system (e.g. amorphous packing); i.e. there is some preferred particle-particle distance, but no recognizable lattice order to longer distances.
Missing Orders
The intensities of higher-order peaks are affected by the exact shape of the structures sitting on the realspace lattice; i.e. the realspace lattice determines the peak positions, while the electron-density distribution within the unit cell controls the peak heights. This modulation of peak heights can be extreme: e.g. an appropriate electron-density distribution can entirely extinguish a particular peak.
This effect can be understood in terms of the form factor modulating the structure factor peak heights. Thus, if a given particle shape (or, more generally, density distribution in the unit cell) has a form-factor minimum at a particular q, then any structural peak at this q will not appear.
For instance, consider a lamellar structure with total layer spacing d; of course we expect reciprocal-space peaks at |q| = 2 π/d, and in fact we expect higher-orders at |q| = n 2 π/d for all integer n. However, for a well-defined two-layer structure where each sub-layer has the same thickness (square-wave density profile), the even-order reflections will be absent. If the two sub-layers have different thicknesses, then the even-order peaks will be present. More generally, the variation in intensity between the odd and even peaks can be used to deduce the duty-cycle.
On the other extreme, consider a 1D repeating structure where the density varies sinusoidally; the higher odd orders will be absent. In fact, a perfectly sinusoidal structure only needs the fundamental Fourier component to completely describe the density-profile. In other words, the higher-order peaks will be entirely absent.
Orientation Distribution
TBD
Crystal Order and Orientation
TBD (amorphous, 3D powder, in-plane powder, single-crystal)