Difference between revisions of "Atomic scattering factors"
KevinYager (talk | contribs) (→See Also) |
KevinYager (talk | contribs) (→Related forms) |
||
| (18 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
==Elemental dependence== | ==Elemental dependence== | ||
| − | Because x-ray interactions occur with an atom's electron cloud, the scattering factors increase with number of electrons, and thus with atomic number (''Z''). However, the relationship between ''f'' and ''Z'' is not monotonic, owing to resonant ([[absorption ]]) edges. | + | Because x-ray interactions occur with an atom's electron cloud, the scattering factors increase with number of electrons, and thus with atomic number (''Z''). However, the relationship between ''f'' and ''Z'' is not monotonic, owing to resonant ([[absorption]]) edges. |
[[Image:Elements-f1.png|400px]][[Image:Elements-f2.png|400px]] | [[Image:Elements-f1.png|400px]][[Image:Elements-f2.png|400px]] | ||
| Line 23: | Line 23: | ||
==Elemental/Energy dependence== | ==Elemental/Energy dependence== | ||
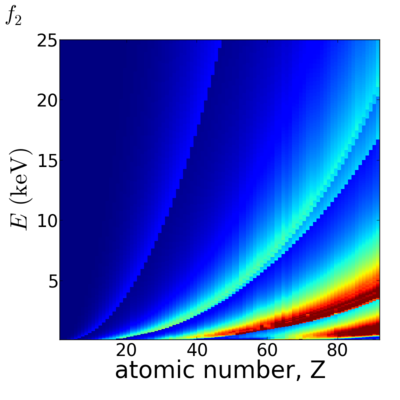
[[Image:Elements2D-f1.png|400px]][[Image:Elements2D-f2.png|400px]] | [[Image:Elements2D-f1.png|400px]][[Image:Elements2D-f2.png|400px]] | ||
| + | |||
| + | ==Related forms== | ||
| + | There are a variety of quantities related to the material's x-ray interaction strength: | ||
| + | * '''Dispersive atomic scattering factor''' <math>f_1</math>, the intrinsic interaction of the material. | ||
| + | * '''[[Critical angle]]''' <math>\theta_c</math>, the angle below which the beam undergoes [[Refractive_index#Total_external_reflection|total external reflection]]. | ||
| + | * '''[[Critical_angle#Critical_q|Critical wave-vector]]''' <math>q_c</math>, the [[momentum transfer]] (in [[reciprocal-space]]) corresponding to the critical angle. | ||
| + | * '''Real [[refractive index]]''' <math>\delta</math>, the refractive component of the refractive index. | ||
| + | * '''Real [[Scattering Length Density]]''' <math>\mathrm{Re}(\mathrm{SLD})</math>, the primary (non-absorptive) component of the scattering contrast. | ||
| + | * '''[[Electron-density distribution|Electron Density]]''' <math>\rho_e</math>, the number of electrons per unit volume. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | <math>f_1</math> | ||
| + | | <math>f_1 = \frac{ \pi M_a}{ \rho N_a r_e \lambda^2 } \theta_c^2</math> | ||
| + | | <math>f_1 = \frac{ M_a}{ 16 \pi \rho N_a r_e } q_c^2</math> | ||
| + | | <math>f_1 = \frac{2 \pi M_a}{ \rho N_a r_e \lambda^2 } \delta</math> | ||
| + | | <math>f_1 = \frac{M_a}{\rho N_a r_e} \mathrm{Re}(\mathrm{SLD}) </math> | ||
| + | | <math> f_1 = \frac{M_a}{\rho N_a} \rho_e</math> | ||
| + | |- | ||
| + | | <math>\theta_c = \sqrt{ \frac{ \rho N_a r_e \lambda^2 }{ \pi M_a} f_1 }</math> | ||
| + | | <math>\theta_c</math> | ||
| + | | <math>\theta_c \approx \frac{\lambda}{4 \pi} q_c </math> | ||
| + | | <math>\theta_c = \sqrt{ 2 \delta }</math> | ||
| + | | <math>\theta_c\approx \sqrt{\frac{\lambda^2 \mathrm{SLD} }{\pi}}</math> | ||
| + | | <math>\theta_c = \sqrt{ \frac{r_e \lambda^2}{\pi} \rho_e }</math> | ||
| + | |- | ||
| + | | <math>q_c = \sqrt{ \frac{ 16 \pi \rho N_a r_e }{ M_a} f_1 }</math> | ||
| + | | <math>q_c = \frac{4 \pi}{\lambda}\sin\theta_c</math> | ||
| + | | <math>q_c</math> | ||
| + | | <math>q_c \approx \frac{4\pi}{\lambda}\sqrt{ 2\delta }</math> | ||
| + | | <math>q_c = \sqrt{ 16 \pi \mathrm{SLD} }</math> | ||
| + | | <math>q_c = 4 \sqrt{ \pi r_e \rho_e}</math> | ||
| + | |- | ||
| + | | <math>\delta = \frac{ \rho N_a r_e \lambda^2 }{2 \pi M_a} f_1</math> | ||
| + | | <math>\delta = \frac{\theta_c^2}{2}</math> | ||
| + | | <math>\delta \approx \frac{\lambda^2}{32 \pi^2}q_c^2</math> | ||
| + | | <math>\delta</math> | ||
| + | | <math>\delta \approx \frac{\lambda^2}{2 \pi}\mathrm{Re}(\mathrm{SLD})</math> | ||
| + | | <math>\delta = \frac{\lambda^2 r_e}{2 \pi} \rho_e</math> | ||
| + | |- | ||
| + | | <math>\mathrm{Re}(\mathrm{SLD}) = \frac{\rho N_a r_e}{M_a} f_1</math> | ||
| + | | <math>\mathrm{Re}(\mathrm{SLD}) \approx \frac{\pi}{\lambda^2}\theta_c^2</math> | ||
| + | | <math>\mathrm{Re}(\mathrm{SLD}) = \frac{q_c^2}{16\pi}</math> | ||
| + | | <math>\mathrm{Re}(\mathrm{SLD}) \approx \frac{2 \pi}{\lambda^2}\delta</math> | ||
| + | | <math>\mathrm{Re}(\mathrm{SLD})</math> | ||
| + | | <math>\mathrm{Re}(\mathrm{SLD}) = r_e \rho_e</math> | ||
| + | |- | ||
| + | | <math>\rho_e = \frac{\rho N_a}{M_a} f_1</math> | ||
| + | | <math>\rho_e = \frac{\pi}{r_e \lambda^2} \theta_c^2</math> | ||
| + | | <math>\rho_e = \frac{q_c^2}{ 16 \pi r_e }</math> | ||
| + | | <math>\rho_e = \frac{2 \pi}{r_e \lambda^2} \delta</math> | ||
| + | | <math>\rho_e = \frac{ \mathrm{Re}(\mathrm{SLD}) }{r_e}</math> | ||
| + | | <math>\rho_e</math> | ||
| + | |} | ||
| + | |||
| + | |||
| + | See also '''[[Absorption_length#Related_forms|absorption length]]''' for a comparison of the quantities related to ''f''<sub>2</sub>. | ||
==See Also== | ==See Also== | ||
| + | * [[Atomic Form Factor]] | ||
* [http://henke.lbl.gov/optical_constants/asf.html Periodic table of atomic scattering factors]: Useful tool for looking up the values for any element. | * [http://henke.lbl.gov/optical_constants/asf.html Periodic table of atomic scattering factors]: Useful tool for looking up the values for any element. | ||
* [https://subversion.xor.aps.anl.gov/trac/pyFprime/ APS Python code for calculating ''f''] | * [https://subversion.xor.aps.anl.gov/trac/pyFprime/ APS Python code for calculating ''f''] | ||
* [http://reference.iucr.org/dictionary/Atomic_scattering_factor Online Dictionary of Crystallography: Atomic scattering factor] | * [http://reference.iucr.org/dictionary/Atomic_scattering_factor Online Dictionary of Crystallography: Atomic scattering factor] | ||
Latest revision as of 14:43, 28 January 2015
The atomic scattering factors are measures of the scattering power of individual atoms. Each element has a different atomic scattering factor, which represents how strongly x-rays interact with those atoms.
The scattering factor has two components: f1 and f2, which describe the dispersive and absorptive components. In other words, f2 describes how strongly the material absorbs the radiation, while f1 describes the non-absorptive interaction (which leads to refraction).
Contents
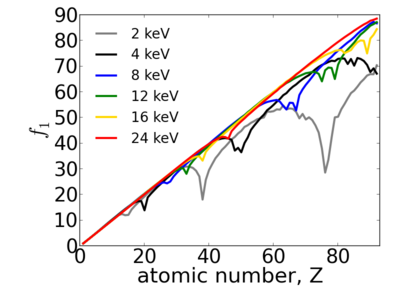
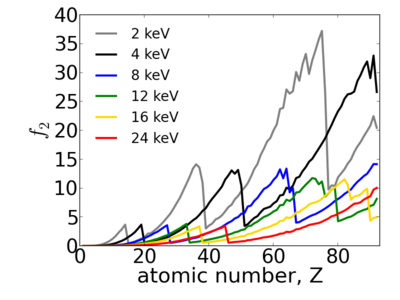
Elemental dependence
Because x-ray interactions occur with an atom's electron cloud, the scattering factors increase with number of electrons, and thus with atomic number (Z). However, the relationship between f and Z is not monotonic, owing to resonant (absorption) edges.
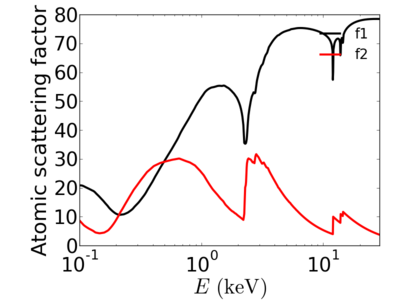
Energy dependence
The atomic scattering factors vary with x-ray wavelength. In particular, a given element will have resonant edges at certain energies, where the absorption increases markedly. The dispersive component f1 will also vary rapidly in the vicinity of an absorption edge (c.f. Kramers-Kronig relations). In general, absorption decreases with increasing energy (i.e. high-energy x-rays can penetrate more efficiently through materials).
Examples
silicon
gold
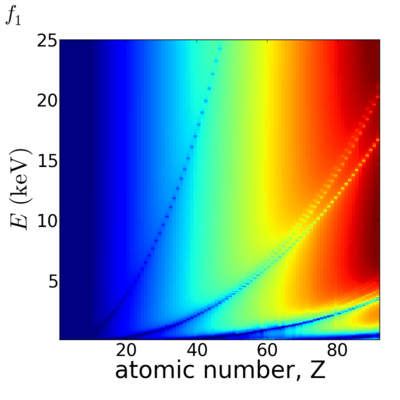
Elemental/Energy dependence
Related forms
There are a variety of quantities related to the material's x-ray interaction strength:
- Dispersive atomic scattering factor , the intrinsic interaction of the material.
- Critical angle , the angle below which the beam undergoes total external reflection.
- Critical wave-vector , the momentum transfer (in reciprocal-space) corresponding to the critical angle.
- Real refractive index , the refractive component of the refractive index.
- Real Scattering Length Density , the primary (non-absorptive) component of the scattering contrast.
- Electron Density , the number of electrons per unit volume.
See also absorption length for a comparison of the quantities related to f2.
See Also
- Atomic Form Factor
- Periodic table of atomic scattering factors: Useful tool for looking up the values for any element.
- APS Python code for calculating f
- Online Dictionary of Crystallography: Atomic scattering factor