Difference between revisions of "Definitional boundaries"
KevinYager (talk | contribs) (→"Kinds" of Scattering) |
KevinYager (talk | contribs) (→See Also) |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
The terms [[diffuse scattering]], [[scattering]], [[diffraction]], [[crystallography]], etc. are used somewhat inconsistently. Traditionally, ''diffraction'' was used to refer to the study of highly crystalline materials, where distinct [[Bragg peak]]s would be observed. If the material was a single-crystal, it would be thought of as ''crystallography'', whereas if it was poly-crystalline, it would be a ''powder diffraction'' experiment. In this context, ''scattering'' was thus implicitly ''diffuse scattering'': the unwanted [[background]] coming from disorder. This is similar to how ''scattering'' is used for visible-light: where ''light scattering'' refers to the diffusion of light through disordered media. ''[[SAXS]]'' (small-angle x-ray scattering) was so-named because traditionally the small-angle regime was used to quantify the diffuse scattering from disordered systems (such as polymers in solution). | The terms [[diffuse scattering]], [[scattering]], [[diffraction]], [[crystallography]], etc. are used somewhat inconsistently. Traditionally, ''diffraction'' was used to refer to the study of highly crystalline materials, where distinct [[Bragg peak]]s would be observed. If the material was a single-crystal, it would be thought of as ''crystallography'', whereas if it was poly-crystalline, it would be a ''powder diffraction'' experiment. In this context, ''scattering'' was thus implicitly ''diffuse scattering'': the unwanted [[background]] coming from disorder. This is similar to how ''scattering'' is used for visible-light: where ''light scattering'' refers to the diffusion of light through disordered media. ''[[SAXS]]'' (small-angle x-ray scattering) was so-named because traditionally the small-angle regime was used to quantify the diffuse scattering from disordered systems (such as polymers in solution). | ||
| − | However, as nanoscience has evolved, a wide variety of well-defined nanoscale structures became available. These structures give rise to well-defined peaks in the small-angle regime; these are diffraction peaks arising from the nano [[superlattice]], strictly analogous to the wide-angle diffraction peaks one obtains for atomic or molecular [[lattices]]/crystals. However, these experiments were historically still called SAXS (or [[SANS]]) experiments, and thus [[GISAXS]] similarly inhereted the term ''scattering'' even | + | However, as nanoscience has evolved, a wide variety of well-defined nanoscale structures became available. These structures give rise to well-defined peaks in the small-angle regime; these are diffraction peaks arising from the nano [[superlattice]], strictly analogous to the wide-angle diffraction peaks one obtains for atomic or molecular [[lattices]]/crystals. However, these experiments were historically still called SAXS (or [[SANS]]) experiments, and thus [[GISAXS]] similarly inhereted the term ''scattering'' even though it was very frequently used to study diffraction [[Scattering features|features]]. (They should have perhaps been called 'small-angle diffraction' experiments.) |
Modern materials may be complex and hierarchical; they are studied simultaneously across a wide ''[[q]]''-range, and may exhibit both diffraction peaks and diffuse scattering in both the small- and wide-angle. It is thus not obvious what to call these experiments or datasets. | Modern materials may be complex and hierarchical; they are studied simultaneously across a wide ''[[q]]''-range, and may exhibit both diffraction peaks and diffuse scattering in both the small- and wide-angle. It is thus not obvious what to call these experiments or datasets. | ||
| − | An evolving trend in the [[x-ray]] and [[neutron]] communities to use the term ''scattering'' as a super-class, which includes all possible experiments where there is an interaction between a sample and radiation. Then, more specific terms can be used to describe the specific kind of experiment/data (diffuse scattering, [[inelastic scattering]], diffraction, crystallography, etc.). However this is not a universal definition, and so 'scattering' remains an ambiguous term (either being shorthand for 'diffuse scattering', or being used to define the broad class of matter-radiation experiments). | + | An evolving trend in the [[x-ray]] and [[neutron]] communities to use the term ''scattering'' as a super-class, which includes all possible experiments where there is an interaction between a sample and radiation. Then, more specific terms can be used to describe the specific kind of experiment/data (diffuse scattering, [[inelastic scattering]], diffraction, crystallography, [[Coherent Diffraction Imaging|coherent imaging]], etc.). However this is not a universal definition, and so 'scattering' remains an ambiguous term (either being shorthand for 'diffuse scattering', or being used to define the broad class of matter-radiation experiments). |
==Angle ranges== | ==Angle ranges== | ||
| Line 111: | Line 111: | ||
* '''Complex objects in disordered states''': Colloids and nanoparticles in solutions, proteins folding/aggregating in solution, [[Example:Polymer_clustering|polymer gels]], etc. In this case, the scattering data is frequently refereed to as ''the'' form factor. Strictly speak, there is still a structure-factor contribution (from which one can deduce inter-particle distances, packing, etc.); but for disordered states, <math>\scriptstyle S(q) \to 1</math> for large ''q''. Thus, at least at large ''q'', the scattering curve is essentially the form factor. Form factors may be indistinct (scaling law), or may have a subtle hump or shoulder. The form factor for monodisperse systems with well-defined shape (e.g. [[Form Factor:Sphere|sphere]]) will have distinct oscillations. | * '''Complex objects in disordered states''': Colloids and nanoparticles in solutions, proteins folding/aggregating in solution, [[Example:Polymer_clustering|polymer gels]], etc. In this case, the scattering data is frequently refereed to as ''the'' form factor. Strictly speak, there is still a structure-factor contribution (from which one can deduce inter-particle distances, packing, etc.); but for disordered states, <math>\scriptstyle S(q) \to 1</math> for large ''q''. Thus, at least at large ''q'', the scattering curve is essentially the form factor. Form factors may be indistinct (scaling law), or may have a subtle hump or shoulder. The form factor for monodisperse systems with well-defined shape (e.g. [[Form Factor:Sphere|sphere]]) will have distinct oscillations. | ||
* '''Simple objects in ordered states''': The perfect single crystals typically measured in [[crystallography]] have atoms (point-like isotropic scatterers) arranged in an ordered [[lattice]]. The resultant scattering is strongly dominated by the structure factor (a.k.a. [[lattice factor]]): sharp [[Bragg peaks]] are observed owing to the constructive interference of scattering from crystal planes that have very well-defined repeat-spacings in [[realspace]]. | * '''Simple objects in ordered states''': The perfect single crystals typically measured in [[crystallography]] have atoms (point-like isotropic scatterers) arranged in an ordered [[lattice]]. The resultant scattering is strongly dominated by the structure factor (a.k.a. [[lattice factor]]): sharp [[Bragg peaks]] are observed owing to the constructive interference of scattering from crystal planes that have very well-defined repeat-spacings in [[realspace]]. | ||
| − | * '''Complex objects in ordered states''': Complex objects can be arranged into well-defined lattices. For instance, nanoparticles (which may have complex shapes, including multi-component structures like core-shell) can be arranged into [[superlattices]]. Self-assembling materials (e.g. [[block-copolymers]]) are another example where one must consider both the symmetry of the lattice, and the shape of the elements sitting on that lattice. In this case, the [[scattering intensity]] has non-negligible contributions from both the structure factor, and the form factor. Analysis of such data can thus be more complicated. | + | * '''Complex objects in ordered states''': Complex objects can be arranged into well-defined lattices. For instance, [[nanoparticles]] (which may have complex shapes, including multi-component structures like core-shell) can be arranged into [[superlattices]]. Self-assembling materials (e.g. [[block-copolymers]]) are another example where one must consider both the symmetry of the lattice, and the shape of the elements sitting on that lattice. In this case, the [[scattering intensity]] has non-negligible contributions from both the structure factor, and the form factor. [[Lattices of nano-objects|Analysis of such data can thus be more complicated]]. |
Again, it must be emphasized that these categories do not have hard boundaries. There is a continuum between all of these states (e.g. a continuous variation from a perfect single-crystal, to a [[paracrystal|disordered crystal]], to a poly-crystal, to an amorphous material, to a gas-like organization). | Again, it must be emphasized that these categories do not have hard boundaries. There is a continuum between all of these states (e.g. a continuous variation from a perfect single-crystal, to a [[paracrystal|disordered crystal]], to a poly-crystal, to an amorphous material, to a gas-like organization). | ||
| Line 177: | Line 177: | ||
|- | |- | ||
|} | |} | ||
| + | |||
| + | ==See Also== | ||
| + | * M. Nespolo, M. I. Aroyo and B. Souvignier [http://scripts.iucr.org/cgi-bin/paper_yard?in5013 Crystallographic shelves: space-group hierarchy explained] ''J. Appl. Cryst.'' '''2018''' [https://doi.org/10.1107/S1600576718012724 doi: 10.1107/S1600576718012724] | ||
| + | * M. Nespolo [http://scripts.iucr.org/cgi-bin/paper?to5189 Lattice versus structure, dimensionality versus periodicity: a crystallographic Babel?] ''J. Appl. Cryst.'' '''2019''', 52. [https://doi.org/10.1107/S1600576719000463 doi: 10.1107/S1600576719000463] | ||
Latest revision as of 10:27, 19 February 2019
As with any technical field, learning about scattering involves absorbing a host of new definitions and jargon. As usual, definitions are not always as clear and consistent as we would like. This page tries to highlight some of the ambiguities.
In the scattering field, the core of the problem is that various techniques were developed to address different limiting cases. However, the fundamental interactions are the same in all cases. As more complex materials began being studied, the resultant data included a mixture of effects; it was no longer so easy to define which 'idealized' experiment one was performing. As instruments have become more versatile, a technique/dataset intended to measure a certain property can now be used to measure many different things. New kinds of samples (nano-materials, aperiodic crystals, etc.) have also upended historical assumptions.
Contents
Scattering Experiments
The terms diffuse scattering, scattering, diffraction, crystallography, etc. are used somewhat inconsistently. Traditionally, diffraction was used to refer to the study of highly crystalline materials, where distinct Bragg peaks would be observed. If the material was a single-crystal, it would be thought of as crystallography, whereas if it was poly-crystalline, it would be a powder diffraction experiment. In this context, scattering was thus implicitly diffuse scattering: the unwanted background coming from disorder. This is similar to how scattering is used for visible-light: where light scattering refers to the diffusion of light through disordered media. SAXS (small-angle x-ray scattering) was so-named because traditionally the small-angle regime was used to quantify the diffuse scattering from disordered systems (such as polymers in solution).
However, as nanoscience has evolved, a wide variety of well-defined nanoscale structures became available. These structures give rise to well-defined peaks in the small-angle regime; these are diffraction peaks arising from the nano superlattice, strictly analogous to the wide-angle diffraction peaks one obtains for atomic or molecular lattices/crystals. However, these experiments were historically still called SAXS (or SANS) experiments, and thus GISAXS similarly inhereted the term scattering even though it was very frequently used to study diffraction features. (They should have perhaps been called 'small-angle diffraction' experiments.)
Modern materials may be complex and hierarchical; they are studied simultaneously across a wide q-range, and may exhibit both diffraction peaks and diffuse scattering in both the small- and wide-angle. It is thus not obvious what to call these experiments or datasets.
An evolving trend in the x-ray and neutron communities to use the term scattering as a super-class, which includes all possible experiments where there is an interaction between a sample and radiation. Then, more specific terms can be used to describe the specific kind of experiment/data (diffuse scattering, inelastic scattering, diffraction, crystallography, coherent imaging, etc.). However this is not a universal definition, and so 'scattering' remains an ambiguous term (either being shorthand for 'diffuse scattering', or being used to define the broad class of matter-radiation experiments).
Angle ranges
There is no unambiguous delineation between WAXS, SAXS, and USAXS. On some instruments, they even define an additional regime: MAXS (Medium-Angle X-ray Scattering) (e.g. if they have a three-detector setup). The following should only be taken as rough guidelines:
| Technique | Angle range | q range | Size range |
|---|---|---|---|
| X-ray backscattering | 180° to 90° | ||
| Diffraction/XRD | 90° to 5° | 6 Å−1 to 0.3 Å−1 | Angstroms to ~2 nm |
| WAXS | 45° to 1° | 5 Å−1 to 0.1 Å−1 | Angstroms to ~6 nm |
| MAXS | 8° to 0.08° | 1 Å−1 to 0.01 Å−1 | ~0.6 nm to ~60 nm |
| SAXS | 1° to 0.01° | 0.1 Å−1 to 0.001 Å−1 | ~6 nm to ~100 nm |
| USAXS | 0.05° to 0.0001° | 0.006 Å−1 to 0.00003 Å−1 | ~100 nm to ~20 µm |
| Technique | Angle range | q range | Size range |
|---|---|---|---|
| Neutron backscattering | 180° to 14° | ||
| Neutron diffraction | 155° to 0.2° | 11 Å−1 to 0.01 Å−1 | Angstroms to ~60 nm |
| WANS | 90° to 4° | 10 Å−1 to 0.1 Å−1 | Angstroms to ~6 nm |
| SANS | 40° to 0.4° | 0.7 Å−1 to 0.008 Å−1 | ~1 nm to ~80 nm |
| VSANS | 0.04° to 0.004° | 0.001 Å−1 to 0.0001 Å−1 | ~600 nm to ~2 µm |
| USANS | 0.2° to 0.00005° | 0.01 Å−1 to 7×10−6 Å−1 | ~60 nm to ~90 µm |
GIXD
Grazing-incidence experiments collecting data at large angles may be called GIWAXS (Grazing-Incidences Wide-Angle X-ray Scattering), or may be called GIXRD/GIXD (Grazing-Incidence X-ray Diffraction), or simply GID. These terms are sometimes used interchangeably. Instrumentally, GIWAXS is typically used to describe collection of wide-angle data with an area detector, whereas GID implies a point or line detector with collimation (i.e. a diffractometer). In terms of materials, GIWAXS may be more appropriate for disordered or partially-ordered materials, whereas GIXRD may be more appropriate for materials with sharp diffraction peaks.
Crystallography
Crystallography typically refers to measuring a single-crystal sample to generate a 2D image with a large number of diffraction peaks. Peak indexing can be used to determine the symmetry and size of the unit cell. The peak intensities can then be used to fit for the probable electron-density distribution within the unit cell; i.e. to solve the crystal structure. Conceptually, a crystal is thus assumed to be a material that has a well-defined unit cell, which is repeated translationally throughout space (normally in all three dimensions). However, the more recent discovery of quasicrystals has forced a rethink of this definition. Quasicrystals do not have translational symmetry, yet they have well-defined local packing that is repeated throughout space, and indeed their diffraction patterns have well-defined peaks. Modernly, a crystal might instead be defined by as an ordered solid that exhibits an essentially discrete diffraction pattern.
- Carlos Basílio Pinheiroa and Artem M. Abakumov Superspace crystallography: a key to the chemistry and properties IUCrJ 2015, 2(1), 137-154. doi: 10.1107/S2052252514023550
"Kinds" of Scattering
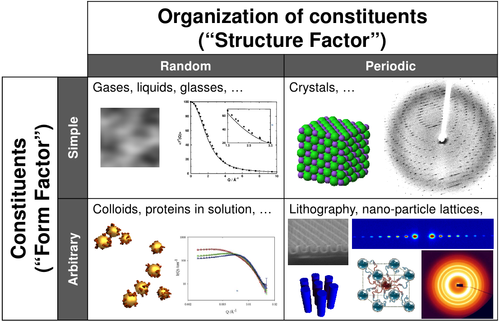
Scattering experts will frequently talk in terms of the Form Factor scattering (which comes from particle shape) or the Structure Factor scattering (which comes from the organization of particles). Although these are discussed as though they are distinct things, in fact they are simply different manifestations of the same fundamental effect: interference of the waves scattered by the material. Thus, there is no perfect separation between these two terms, and there are samples for which a clear delineation into the two kinds of scattering is not possible. Nevertheless, these definitions are helpful in organizing one's thoughts about scattering experiments.
One can roughly think of scattering experiments of four kinds:
- Simple objects in disordered states: Gases, liquid, glasses, etc. are highly disordered. The constituents are simple and their scattering can be thought of as point-like and isotropic (at least for the q-ranges typically probed). The resultant scattering data is one-dimensional, and does not have any sharp peaks. Instead, there is a continuous intensity variation (which may be described as diffuse scattering). Nevertheless, these kinds of scattering curves can be fit to scaling relationships, in order to extract parameters of interest.
- Complex objects in disordered states: Colloids and nanoparticles in solutions, proteins folding/aggregating in solution, polymer gels, etc. In this case, the scattering data is frequently refereed to as the form factor. Strictly speak, there is still a structure-factor contribution (from which one can deduce inter-particle distances, packing, etc.); but for disordered states, for large q. Thus, at least at large q, the scattering curve is essentially the form factor. Form factors may be indistinct (scaling law), or may have a subtle hump or shoulder. The form factor for monodisperse systems with well-defined shape (e.g. sphere) will have distinct oscillations.
- Simple objects in ordered states: The perfect single crystals typically measured in crystallography have atoms (point-like isotropic scatterers) arranged in an ordered lattice. The resultant scattering is strongly dominated by the structure factor (a.k.a. lattice factor): sharp Bragg peaks are observed owing to the constructive interference of scattering from crystal planes that have very well-defined repeat-spacings in realspace.
- Complex objects in ordered states: Complex objects can be arranged into well-defined lattices. For instance, nanoparticles (which may have complex shapes, including multi-component structures like core-shell) can be arranged into superlattices. Self-assembling materials (e.g. block-copolymers) are another example where one must consider both the symmetry of the lattice, and the shape of the elements sitting on that lattice. In this case, the scattering intensity has non-negligible contributions from both the structure factor, and the form factor. Analysis of such data can thus be more complicated.
Again, it must be emphasized that these categories do not have hard boundaries. There is a continuum between all of these states (e.g. a continuous variation from a perfect single-crystal, to a disordered crystal, to a poly-crystal, to an amorphous material, to a gas-like organization).
Energy
X-ray energies are frequently referred to as 'hard' (for high-energy x-rays) or 'soft' (for low-energy x-rays). 'Tender' refers to the cross-over between hard and soft x-rays. There is no sharp definition for these terms. The following roughly establishes the terms for different photon energies:
| Term | Energy range | Wavelength range | |
|---|---|---|---|
| Far Infrared | IR | 1.2 meV to 12 meV | 1,000 µm to 100 µm |
| Mid Infrared | IR | 12 meV to 124 meV | 100 µm to 10 µm |
| Near Infrared | NIR | 124 meV to 1.77 eV | 10 µm to 700 nm |
| Visible Light | VIS | 1.77 eV to 3.13 eV | 700 nm to 400 nm |
| Near Ultraviolet | UV | 3.13 eV to 12 eV | 400 nm to 100 nm |
| Extreme Ultraviolet | EUV | 12 eV to 124 eV | 100 nm to 10 nm |
| Soft X-rays | SoX | 124 eV to 6 keV | 10 nm to 2 Å |
| Tender X-rays | 1 keV to 10 keV | 12 Å to 1.2 Å | |
| Hard X-rays | X-ray | 8 keV to 124 keV | 1.6 Å to 0.1 Å |
| Gamma rays | γ | 124 keV to >1.2 MeV | 0.1 Å to <0.01 Å |
See Also
- M. Nespolo, M. I. Aroyo and B. Souvignier Crystallographic shelves: space-group hierarchy explained J. Appl. Cryst. 2018 doi: 10.1107/S1600576718012724
- M. Nespolo Lattice versus structure, dimensionality versus periodicity: a crystallographic Babel? J. Appl. Cryst. 2019, 52. doi: 10.1107/S1600576719000463