Difference between revisions of "Critical angle"
KevinYager (talk | contribs) |
KevinYager (talk | contribs) (→See Also) |
||
| (22 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | In [[GISAXS]], the '''critical angle''' for a thin film is the incident angle below which one gets total external reflection of the x-ray beam. | + | In [[GISAXS]], the '''critical angle''' for a thin film is the incident angle below which one gets [[Refractive_index#Total_external_reflection|total external reflection]] of the x-ray beam. |
| − | Below the critical angle, the beam is fully reflected from the film. The x-ray field probes a short distance into the film surface (due to the evanescent wave); on the order of a few nanometers. Thus, a GISAXS measurement below the critical angle is inherently probing only the film surface. A measurement well above the critical angle, by comparison, penetrates through the film and thus measures the average of the structure through the whole film. Close to the critical angle, the refracted beam is nearly parallel to the film interface; in other words the beam is coupled into [[X-ray waveguide|waveguide]] modes. This increases the effective path-length of the beam through the sample, which thereby increases the intensity of the scattering. | + | Below the critical angle, the beam is fully reflected from the film. The x-ray field probes a short distance into the film surface (due to the evanescent wave); on the order of a few nanometers. Thus, a GISAXS measurement below the critical angle is inherently probing only the film surface. A measurement well above the critical angle, by comparison, penetrates through the film and thus measures the average of the structure through the whole film. Close to the critical angle, the [[Refraction distortion|refracted beam]] is nearly parallel to the film interface; in other words the beam is coupled into [[X-ray waveguide|waveguide]] modes. This increases the effective path-length of the beam through the sample, which thereby increases the intensity of the [[scattering]]. |
| − | Normally in GISAXS experiments, it is useful to do measurements both below and above the critical angle; by comparing the two patterns, you can ascertain whether the structures observed at the surface (e.g. as seen by AFM or SEM) are representative of the entire film. Measurements close to the critical angle are useful because of the intensity enhancement. | + | Normally in GISAXS experiments, it is useful to do measurements both below and above the critical angle; by comparing the two patterns, you can ascertain whether the structures observed at the surface (e.g. as seen by AFM or SEM) are representative of the entire film. Measurements close to the critical angle are useful because of the [[GISAXS#Intensity_Enhancement|intensity enhancement]]. |
==Examples== | ==Examples== | ||
| + | |||
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| Line 14: | Line 15: | ||
! critical angle (°) | ! critical angle (°) | ||
! ''q<sub>c</sub>'' (Å<sup>−1</sup>) | ! ''q<sub>c</sub>'' (Å<sup>−1</sup>) | ||
| + | ! SLD (10<sup>−6</sup>Å<sup>−2</sup>) | ||
| + | |- | ||
| + | | [[Material:Polystyrene|polystyrene]] | ||
| + | | 1.00 | ||
| + | | 2.0 | ||
| + | | 6.20 | ||
| + | | 0.613 | ||
| + | | 0.0217 | ||
| + | | 9.34 | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | 4.0 | ||
| + | | 3.10 | ||
| + | | 0.304 | ||
| + | | 0.0215 | ||
| + | | 9.21 | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | 8.0 | ||
| + | | 1.55 | ||
| + | | 0.152 | ||
| + | | 0.0214 | ||
| + | | 9.15 | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | 12.0 | ||
| + | | 1.03 | ||
| + | | 0.101 | ||
| + | | 0.0214 | ||
| + | | 9.13 | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | 16.0 | ||
| + | | 0.77 | ||
| + | | 0.076 | ||
| + | | 0.0214 | ||
| + | | 9.13 | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | 24.0 | ||
| + | | 0.52 | ||
| + | | 0.050 | ||
| + | | 0.0214 | ||
| + | | 9.12 | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Material | ||
| + | ! density (g/cm<sup>3</sup>) | ||
| + | ! X-ray energy (keV) | ||
| + | ! X-ray wavelength (Å) | ||
| + | ! critical angle (°) | ||
| + | ! ''q<sub>c</sub>'' (Å<sup>−1</sup>) | ||
| + | ! SLD (10<sup>−6</sup>Å<sup>−2</sup>) | ||
|- | |- | ||
| [[Material:Silicon|Si]] | | [[Material:Silicon|Si]] | ||
| Line 21: | Line 82: | ||
| 0.824 | | 0.824 | ||
| 0.0291 | | 0.0291 | ||
| + | | 16.89 | ||
|- | |- | ||
| | | | ||
| Line 28: | Line 90: | ||
| 0.451 | | 0.451 | ||
| 0.0319 | | 0.0319 | ||
| + | | 20.28 | ||
|- | |- | ||
| | | | ||
| Line 35: | Line 98: | ||
| 0.224 | | 0.224 | ||
| 0.0317 | | 0.0317 | ||
| + | | 20.07 | ||
|- | |- | ||
| | | | ||
| Line 42: | Line 106: | ||
| 0.149 | | 0.149 | ||
| 0.0317 | | 0.0317 | ||
| + | | 19.92 | ||
|- | |- | ||
| Line 50: | Line 115: | ||
| 0.112 | | 0.112 | ||
| 0.0316 | | 0.0316 | ||
| + | | 19.84 | ||
|- | |- | ||
| | | | ||
| Line 57: | Line 123: | ||
| 0.07426 | | 0.07426 | ||
| 0.0315 | | 0.0315 | ||
| + | | 19.77 | ||
|- | |- | ||
|} | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Material | ||
| + | ! density (g/cm<sup>3</sup>) | ||
| + | ! X-ray energy (keV) | ||
| + | ! X-ray wavelength (Å) | ||
| + | ! critical angle (°) | ||
| + | ! ''q<sub>c</sub>'' (Å<sup>−1</sup>) | ||
| + | ! SLD (10<sup>−6</sup>Å<sup>−2</sup>) | ||
| + | |- | ||
| + | | [[Material:Silicon dioxide|SiO2]] | ||
| + | | 2.648 | ||
| + | | 2.0 | ||
| + | | 6.20 | ||
| + | | 0.927 | ||
| + | | 0.0328 | ||
| + | | 21.42 | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | 4.0 | ||
| + | | 3.10 | ||
| + | | 0.480 | ||
| + | | 0.0340 | ||
| + | | 22.96 | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | 8.0 | ||
| + | | 1.55 | ||
| + | | 0.239 | ||
| + | | 0.0338 | ||
| + | | 22.71 | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | 12.0 | ||
| + | | 1.03 | ||
| + | | 0.159 | ||
| + | | 0.0337 | ||
| + | | 22.58 | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | 16.0 | ||
| + | | 0.77 | ||
| + | | 0.119 | ||
| + | | 0.0337 | ||
| + | | 22.53 | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | 24.0 | ||
| + | | 0.52 | ||
| + | | 0.079 | ||
| + | | 0.0336 | ||
| + | | 22.48 | ||
| + | |} | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Material | ||
| + | ! density (g/cm<sup>3</sup>) | ||
| + | ! X-ray energy (keV) | ||
| + | ! X-ray wavelength (Å) | ||
| + | ! critical angle (°) | ||
| + | ! ''q<sub>c</sub>'' (Å<sup>−1</sup>) | ||
| + | ! SLD (10<sup>−6</sup>Å<sup>−2</sup>) | ||
| + | |- | ||
| + | | [[Material:Gold|Au]] | ||
| + | | 19.32 | ||
| + | | 2.0 | ||
| + | | 6.20 | ||
| + | | 1.830 | ||
| + | | 0.0647 | ||
| + | | 83.44 | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | 4.0 | ||
| + | | 3.10 | ||
| + | | 1.097 | ||
| + | | 0.0776 | ||
| + | | 119.89 | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | 8.0 | ||
| + | | 1.55 | ||
| + | | 0.560 | ||
| + | | 0.0792 | ||
| + | | 124.86 | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | 12.0 | ||
| + | | 1.03 | ||
| + | | 0.348 | ||
| + | | 0.0738 | ||
| + | | 108.29 | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | 16.0 | ||
| + | | 0.77 | ||
| + | | 0.282 | ||
| + | | 0.0797 | ||
| + | | 126.51 | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | 24.0 | ||
| + | | 0.52 | ||
| + | | 0.191 | ||
| + | | 0.0811 | ||
| + | | 130.80 | ||
| + | |} | ||
| + | |||
| + | ==Critical ''q''== | ||
| + | The critical angle can be converted into a critical [[momentum transfer]]. In reflection-mode, the scattering vector is: | ||
| + | :<math> \begin{alignat}{2} | ||
| + | \mathbf{q} & = \mathbf{k}_o-\mathbf{k}_i \\ | ||
| + | |\mathbf{q}| & = q = 2 |k| \sin\theta_i = \frac{4 \pi}{\lambda}\sin\theta_i | ||
| + | \end{alignat} | ||
| + | </math> | ||
| + | Where ''λ'' is the wavelength of the x-rays. So, the critical ''q'' in [[reciprocal-space]] is: | ||
| + | :<math> | ||
| + | q_c = \frac{4 \pi}{\lambda}\sin\theta_c | ||
| + | </math> | ||
| + | The critical ''q'' somewhat factors-out the influence of x-ray energy, making ''q<sub>c</sub>'' less sensitive to variations in energy. However, even ''q<sub>c</sub>'' strictly has an energy-dependence. | ||
==Calculating== | ==Calculating== | ||
| Line 65: | Line 263: | ||
The [[Scattering Length Density]] (SLD) for any given material can be computed using tabulated values. From this, the critical angle can be computed. The critical scattering vector is: | The [[Scattering Length Density]] (SLD) for any given material can be computed using tabulated values. From this, the critical angle can be computed. The critical scattering vector is: | ||
:<math>q_c = \sqrt{ 16 \pi \mathrm{SLD} }</math> | :<math>q_c = \sqrt{ 16 \pi \mathrm{SLD} }</math> | ||
| − | + | So: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
:<math> | :<math> | ||
\begin{alignat}{2} | \begin{alignat}{2} | ||
| Line 81: | Line 273: | ||
===From refractive index=== | ===From refractive index=== | ||
| − | The critical angle is simply a result of the refractive index contrast between the film and the ambient. Of course, in this case we are talking about the '''x-ray refractive index''' (not the usual refractive index for visible light). In the case of neutrons, the film similarly exhibits a neutron refractive index. The refractive index is complex: | + | The critical angle is simply a result of the [[refractive index]] contrast between the film and the ambient. Of course, in this case we are talking about the '''x-ray [[refractive index]]''' (not the usual refractive index for visible light). In the case of neutrons, the film similarly exhibits a neutron refractive index. The refractive index is complex: |
:<math> | :<math> | ||
n = 1 - \delta + i \beta | n = 1 - \delta + i \beta | ||
| Line 102: | Line 294: | ||
\theta_c = \sqrt{ 2 \delta } | \theta_c = \sqrt{ 2 \delta } | ||
</math> | </math> | ||
| − | Note that the resultant critical angle has units of ''radians''. For a multi-component system, one simply | + | Note that the resultant critical angle has units of ''radians''. For a multi-component system, one simply uses a weighted sum of the contributions from each element: |
:<math> | :<math> | ||
| − | \theta_c = \sqrt{ \frac{\rho N_a r_e \lambda^2 \sum_{i=1}^{N} f_{1i} }{ \pi \sum_{i=1}^{N} M_i } } | + | \theta_c = \sqrt{ \frac{\rho N_a r_e \lambda^2 \sum_{i=1}^{N} c_i f_{1i} }{ \pi \sum_{i=1}^{N} c_i M_i } } |
</math> | </math> | ||
| + | where the ''c<sub>i</sub>'' the weighting factors (concentration, or stoichiometric numbers in a chemical formula). | ||
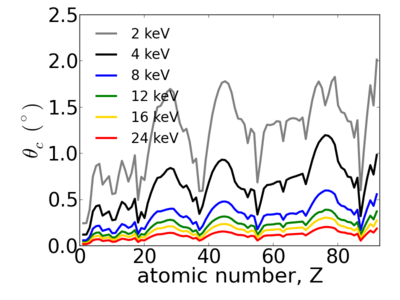
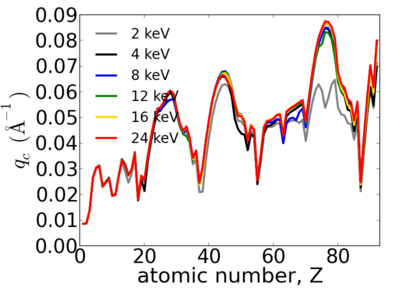
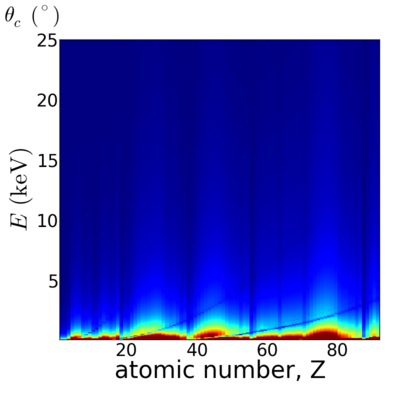
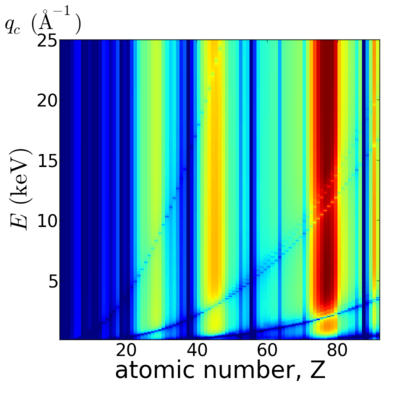
| − | == | + | ==Elemental dependence== |
| − | The critical angle | + | |
| + | [[Image:Elements-crit.png|400px]][[Image:Elements-critq.png|400px]] | ||
| + | |||
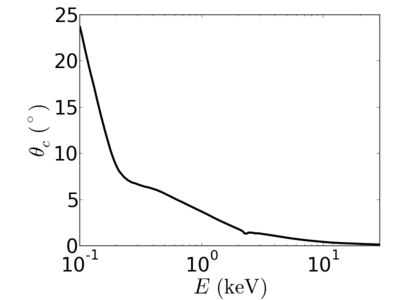
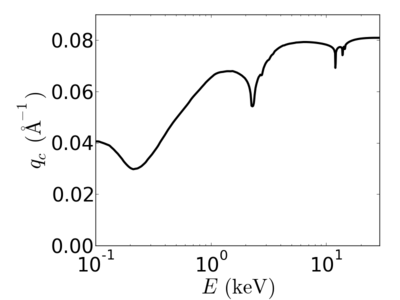
| + | ==Energy dependence== | ||
| + | The critical angle depends on the real part of the refractive index. In general, high-energy (short wavelength) x-rays are more weakly refracted, giving rise to a smaller critical angle. | ||
| + | |||
| + | ===Examples=== | ||
| + | |||
| + | ====[[Material:Silicon|silicon]]==== | ||
| + | |||
| + | [[Image:Silicon-crit.png|400px]][[Image:Silicon-critq.png|400px]] | ||
| + | |||
| + | ====[[Material:Gold|gold]]==== | ||
| + | |||
| + | [[Image:Gold-crit.png|400px]][[Image:Gold-critq.png|400px]] | ||
| + | ==Elemental/Energy dependence== | ||
| + | [[Image:Elements2D-crit.png|400px]][[Image:Elements2D-critq.png|400px]] | ||
| − | [[ | + | ==See Also== |
| + | * [[Scattering Length Density]] | ||
| + | * [[Refractive index]] | ||
| + | ** [http://henke.lbl.gov/optical_constants/getdb2.html CXRO refractive index calculator] | ||
| + | * [http://en.wikipedia.org/wiki/Evanescent_wave Wikipedia: Evanescent wave] | ||
Latest revision as of 15:28, 21 March 2019
In GISAXS, the critical angle for a thin film is the incident angle below which one gets total external reflection of the x-ray beam.
Below the critical angle, the beam is fully reflected from the film. The x-ray field probes a short distance into the film surface (due to the evanescent wave); on the order of a few nanometers. Thus, a GISAXS measurement below the critical angle is inherently probing only the film surface. A measurement well above the critical angle, by comparison, penetrates through the film and thus measures the average of the structure through the whole film. Close to the critical angle, the refracted beam is nearly parallel to the film interface; in other words the beam is coupled into waveguide modes. This increases the effective path-length of the beam through the sample, which thereby increases the intensity of the scattering.
Normally in GISAXS experiments, it is useful to do measurements both below and above the critical angle; by comparing the two patterns, you can ascertain whether the structures observed at the surface (e.g. as seen by AFM or SEM) are representative of the entire film. Measurements close to the critical angle are useful because of the intensity enhancement.
Contents
Examples
| Material | density (g/cm3) | X-ray energy (keV) | X-ray wavelength (Å) | critical angle (°) | qc (Å−1) | SLD (10−6Å−2) |
|---|---|---|---|---|---|---|
| polystyrene | 1.00 | 2.0 | 6.20 | 0.613 | 0.0217 | 9.34 |
| 4.0 | 3.10 | 0.304 | 0.0215 | 9.21 | ||
| 8.0 | 1.55 | 0.152 | 0.0214 | 9.15 | ||
| 12.0 | 1.03 | 0.101 | 0.0214 | 9.13 | ||
| 16.0 | 0.77 | 0.076 | 0.0214 | 9.13 | ||
| 24.0 | 0.52 | 0.050 | 0.0214 | 9.12 |
| Material | density (g/cm3) | X-ray energy (keV) | X-ray wavelength (Å) | critical angle (°) | qc (Å−1) | SLD (10−6Å−2) |
|---|---|---|---|---|---|---|
| Si | 2.3290 | 2.0 | 6.20 | 0.824 | 0.0291 | 16.89 |
| 4.0 | 3.10 | 0.451 | 0.0319 | 20.28 | ||
| 8.0 | 1.55 | 0.224 | 0.0317 | 20.07 | ||
| 12.0 | 1.03 | 0.149 | 0.0317 | 19.92 | ||
| 16.0 | 0.77 | 0.112 | 0.0316 | 19.84 | ||
| 24.0 | 0.52 | 0.07426 | 0.0315 | 19.77 |
| Material | density (g/cm3) | X-ray energy (keV) | X-ray wavelength (Å) | critical angle (°) | qc (Å−1) | SLD (10−6Å−2) |
|---|---|---|---|---|---|---|
| SiO2 | 2.648 | 2.0 | 6.20 | 0.927 | 0.0328 | 21.42 |
| 4.0 | 3.10 | 0.480 | 0.0340 | 22.96 | ||
| 8.0 | 1.55 | 0.239 | 0.0338 | 22.71 | ||
| 12.0 | 1.03 | 0.159 | 0.0337 | 22.58 | ||
| 16.0 | 0.77 | 0.119 | 0.0337 | 22.53 | ||
| 24.0 | 0.52 | 0.079 | 0.0336 | 22.48 |
| Material | density (g/cm3) | X-ray energy (keV) | X-ray wavelength (Å) | critical angle (°) | qc (Å−1) | SLD (10−6Å−2) |
|---|---|---|---|---|---|---|
| Au | 19.32 | 2.0 | 6.20 | 1.830 | 0.0647 | 83.44 |
| 4.0 | 3.10 | 1.097 | 0.0776 | 119.89 | ||
| 8.0 | 1.55 | 0.560 | 0.0792 | 124.86 | ||
| 12.0 | 1.03 | 0.348 | 0.0738 | 108.29 | ||
| 16.0 | 0.77 | 0.282 | 0.0797 | 126.51 | ||
| 24.0 | 0.52 | 0.191 | 0.0811 | 130.80 |
Critical q
The critical angle can be converted into a critical momentum transfer. In reflection-mode, the scattering vector is:
Where λ is the wavelength of the x-rays. So, the critical q in reciprocal-space is:
The critical q somewhat factors-out the influence of x-ray energy, making qc less sensitive to variations in energy. However, even qc strictly has an energy-dependence.
Calculating
The critical angle for a material can be calculated in a variety of ways. For an elemental substance, this online tool will calculate it for you.
From SLD
The Scattering Length Density (SLD) for any given material can be computed using tabulated values. From this, the critical angle can be computed. The critical scattering vector is:
So:
From refractive index
The critical angle is simply a result of the refractive index contrast between the film and the ambient. Of course, in this case we are talking about the x-ray refractive index (not the usual refractive index for visible light). In the case of neutrons, the film similarly exhibits a neutron refractive index. The refractive index is complex:
For x-rays, the values of 𝛿 and β can be calculated from the atomic scattering factors (f1 and f2) using:
Where re is the classical electron radius (2.8179403x10−15 m), λ is the wavelength of the probing x-rays, and na is the number density:
where ρ is the physical density (e.g. in g/cm3), Na is the Avogadro constant (6.02214129x1023 mol−1), and Ma is molar mass (e.g. in g/mol). There are also online tools that will compute the refractive index for you.
Once the real part of the refractive index (𝛿) is known, conversion to critical angle is straightforward:
Note that the resultant critical angle has units of radians. For a multi-component system, one simply uses a weighted sum of the contributions from each element:
where the ci the weighting factors (concentration, or stoichiometric numbers in a chemical formula).
Elemental dependence
Energy dependence
The critical angle depends on the real part of the refractive index. In general, high-energy (short wavelength) x-rays are more weakly refracted, giving rise to a smaller critical angle.