Difference between revisions of "Lattices"
KevinYager (talk | contribs) (→Hexagonal) |
KevinYager (talk | contribs) (→See Also) |
||
| (14 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
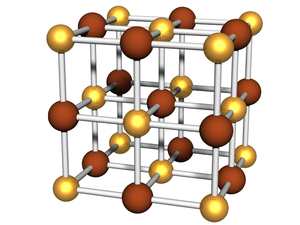
[[Image:Bcc03-lattice.png|thumb|right|300px|Example of a [[Lattice:BCC|BCC]] lattice.]] | [[Image:Bcc03-lattice.png|thumb|right|300px|Example of a [[Lattice:BCC|BCC]] lattice.]] | ||
| − | In x-ray scattering, we frequently study materials which have constituents arranged on a well-defined '''lattice'''. For instance, an atomic crystal has atoms which occupy well-defined sites within a representative [[unit cell]], which then repeats in all three directions throughout space. Nanoparticle superlattices are a nanoscale analogue, where each lattice site is occupied by a nanoparticle. Other kinds of nanostructures systems can be considered similarly. [[Block-copolymers|Block-copolymer]] mesophases can be thought of as nanostructures sitting on lattice sites (e.g. cylinders in a hexagonal lattice). | + | In x-ray scattering, we frequently study materials which have constituents arranged on a well-defined '''lattice'''. For instance, an atomic crystal has atoms which occupy well-defined sites within a representative [[unit cell]], which then repeats in all three directions throughout space. Nanoparticle [[superlattices]] are a nanoscale analogue, where each lattice site is occupied by a nanoparticle. Other kinds of nanostructures systems can be considered similarly. [[Block-copolymers|Block-copolymer]] mesophases can be thought of as nanostructures sitting on lattice sites (e.g. cylinders in a hexagonal lattice). |
| − | Well- | + | Well-defined [[realspace]] lattices (repeating structures) [[Fourier transform|give rise]] to well-defined peaks in [[reciprocal-space]], which makes it possible to determine the realspace lattice by considering the arrangement (symmetry) of the [[scattering]] peaks. |
==Notation== | ==Notation== | ||
| − | * '''Real space''': | + | * '''[[Real space]]''': |
** Crystal ''planes'': | ** Crystal ''planes'': | ||
*** (hkl) denotes a plane of the crystal structure (and repetitions of that plane, with the given spacing). In cubic systems (but not others), the normal to the plane is [hkl] | *** (hkl) denotes a plane of the crystal structure (and repetitions of that plane, with the given spacing). In cubic systems (but not others), the normal to the plane is [hkl] | ||
| Line 25: | Line 25: | ||
==Lattices== | ==Lattices== | ||
| + | [[Image:Sc01.png|thumb|right|300px|Example of an alternating simple cubic (NaCl) lattice.]] | ||
===Cubic=== | ===Cubic=== | ||
There are three [http://en.wikipedia.org/wiki/Cubic_crystal_system cubic] space groups: | There are three [http://en.wikipedia.org/wiki/Cubic_crystal_system cubic] space groups: | ||
* [[Lattice:Simple_cubic|Simple cubic (SC)]] | * [[Lattice:Simple_cubic|Simple cubic (SC)]] | ||
| + | ** [[Lattice:Simple_cubic#Alternating_Simple_Cubic|Alternating simple cubic (NaCl)]] | ||
* [[Lattice:BCC|Body-centered cubic (BCC)]] | * [[Lattice:BCC|Body-centered cubic (BCC)]] | ||
| + | ** [[Lattice:BCC#Body-centered_Two-particle|CsCl]] | ||
* [[Lattice:FCC|Face-centered cubic (FCC)]] | * [[Lattice:FCC|Face-centered cubic (FCC)]] | ||
There are many conceptually distinct lattices that exhibit one of the above cubic symmetries: | There are many conceptually distinct lattices that exhibit one of the above cubic symmetries: | ||
* [[Lattice:Diamond|Diamond lattice]] (FCC) | * [[Lattice:Diamond|Diamond lattice]] (FCC) | ||
| + | ** [[Lattice:NaTl|B32 (NaTl)]] | ||
===Hexagonal=== | ===Hexagonal=== | ||
| Line 38: | Line 42: | ||
** [[Lattice:Hexagonal diamond|Hexagonal diamond]] | ** [[Lattice:Hexagonal diamond|Hexagonal diamond]] | ||
*** [[Lattice:Wurtzite|Wurtzite]] | *** [[Lattice:Wurtzite|Wurtzite]] | ||
| − | ** [[Lattice:AlB2]] | + | ** [[Lattice:AlB2|AlB<sub>2</sub>]] |
| + | |||
| + | ==Symmetry and Space Groups== | ||
| + | * U. Shmueli, S. R. Hall and R. W. Grosse-Kunstleve, [http://www.springerlink.com/content/p64698026200453u/ Symmetry in reciprocal space] International Tables for Crystallography Volume B: Reciprocal space, 1, Springer 2001 pp 99-161 ISSN 1574-8707 ISBN 978-0-7923-6592-1 (Print) 978-1-4020-5407-5 (Online) [http://dx.doi.org/10.1107/97809553602060000552 doi 10.1107/97809553602060000552] | ||
| + | |||
| + | ==Peak Positions== | ||
| + | ===Cubic=== | ||
| + | :<math>\frac{1}{d_{hkl}^2} = \frac{h^2 + k^2 + l^2}{a^2} </math> | ||
| + | :<math>q_{hkl} = 2 \pi \left( \frac{h^2 + k^2 + l^2}{a^2} \right)^{1/2}</math> | ||
| + | |||
| + | ===Hexagonal=== | ||
| + | : <math>\frac{1}{d_{hkl}^2} = \frac{4}{3} \left( \frac{h^2 + hk + k^2}{a^2} \right) + \frac{l^2}{c^2} </math> | ||
| + | : <math>q_{hkl}=2\pi\left( \frac{4(h^2 + hk + k^2)}{3a^2} + \frac{l^2}{c^2} \right)^{1/2}</math> | ||
| + | |||
| + | ===Tetragonal=== | ||
| + | : <math>\frac{1}{d_{hkl}^2} = \frac{h^2 + k^2}{a^2} + \frac{l^2}{c^2} </math> | ||
| + | : <math>q_{hkl} = 2\pi \left ( \frac{h^2 + k^2}{a^2} + \frac{l^2}{c^2} \right )^{1/2} </math> | ||
| + | |||
| + | ===Orthorhombic=== | ||
| + | : <math>\frac{1}{d_{hkl}^2} = \frac{h^2}{a^2} + \frac{k^2}{b^2} + \frac{l^2}{c^2} </math> | ||
| + | : <math>q_{hkl}^2 = 2\pi \left ( \frac{h^2}{a^2} + \frac{k^2}{b^2} + \frac{l^2}{c^2} \right )^{1/2} </math> | ||
==See Also== | ==See Also== | ||
* [http://en.wikipedia.org/wiki/Crystal_structure Wikipedia: Crystal Structure] | * [http://en.wikipedia.org/wiki/Crystal_structure Wikipedia: Crystal Structure] | ||
| + | * [[Unit cell]] | ||
* [[Lattice:Packing fraction]] | * [[Lattice:Packing fraction]] | ||
| + | * [[Lattices of nano-objects]] | ||
| + | * [http://www.cryst.ehu.es/html/cryst/magnext.php?from=magnext&magtr=9 Space Group List] | ||
| + | * M. Nespolo, M. I. Aroyo and B. Souvignier [http://scripts.iucr.org/cgi-bin/paper_yard?in5013 Crystallographic shelves: space-group hierarchy explained] ''J. Appl. Cryst.'' '''2018''' [https://doi.org/10.1107/S1600576718012724 doi: 10.1107/S1600576718012724] | ||
| + | * M. Nespolo [http://scripts.iucr.org/cgi-bin/paper?to5189 Lattice versus structure, dimensionality versus periodicity: a crystallographic Babel?] ''J. Appl. Cryst.'' '''2019''', 52. [https://doi.org/10.1107/S1600576719000463 doi: 10.1107/S1600576719000463] | ||
Latest revision as of 10:27, 19 February 2019
In x-ray scattering, we frequently study materials which have constituents arranged on a well-defined lattice. For instance, an atomic crystal has atoms which occupy well-defined sites within a representative unit cell, which then repeats in all three directions throughout space. Nanoparticle superlattices are a nanoscale analogue, where each lattice site is occupied by a nanoparticle. Other kinds of nanostructures systems can be considered similarly. Block-copolymer mesophases can be thought of as nanostructures sitting on lattice sites (e.g. cylinders in a hexagonal lattice).
Well-defined realspace lattices (repeating structures) give rise to well-defined peaks in reciprocal-space, which makes it possible to determine the realspace lattice by considering the arrangement (symmetry) of the scattering peaks.
Contents
Notation
- Real space:
- Crystal planes:
- (hkl) denotes a plane of the crystal structure (and repetitions of that plane, with the given spacing). In cubic systems (but not others), the normal to the plane is [hkl]
- {hkl} denotes the set of all planes that are equivalent to (hkl) by the symmetry of the lattice
- Crystal directions:
- [hkl] denotes a direction of a vector (in the basis of the direct lattice vectors)
- denotes the set of all directions that are equivalent to [hkl] by symmetry (e.g. in cubic system 〈100〉 means [100], [010], [001], [-100], [0-10], [00-1])
- hkl denotes a diffracting plane
- Crystal planes:
- Reciprocal space:
- Reciprocal planes:
- [hkl] denotes a plane
- denotes the set of all planes that are equivalent to [hkl]
- Reciprocal directions:
- (hkl) denotes a particular direction (normal to plane (hkl) in real space)
- {hkl} denotes the set of all directions that are equivalent to (hkl)
- hkl denotes an indexed reflection
- Reciprocal planes:
Lattices
Cubic
There are three cubic space groups:
There are many conceptually distinct lattices that exhibit one of the above cubic symmetries:
- Diamond lattice (FCC)
Hexagonal
Symmetry and Space Groups
- U. Shmueli, S. R. Hall and R. W. Grosse-Kunstleve, Symmetry in reciprocal space International Tables for Crystallography Volume B: Reciprocal space, 1, Springer 2001 pp 99-161 ISSN 1574-8707 ISBN 978-0-7923-6592-1 (Print) 978-1-4020-5407-5 (Online) doi 10.1107/97809553602060000552
Peak Positions
Cubic
Hexagonal
Tetragonal
Orthorhombic
See Also
- Wikipedia: Crystal Structure
- Unit cell
- Lattice:Packing fraction
- Lattices of nano-objects
- Space Group List
- M. Nespolo, M. I. Aroyo and B. Souvignier Crystallographic shelves: space-group hierarchy explained J. Appl. Cryst. 2018 doi: 10.1107/S1600576718012724
- M. Nespolo Lattice versus structure, dimensionality versus periodicity: a crystallographic Babel? J. Appl. Cryst. 2019, 52. doi: 10.1107/S1600576719000463